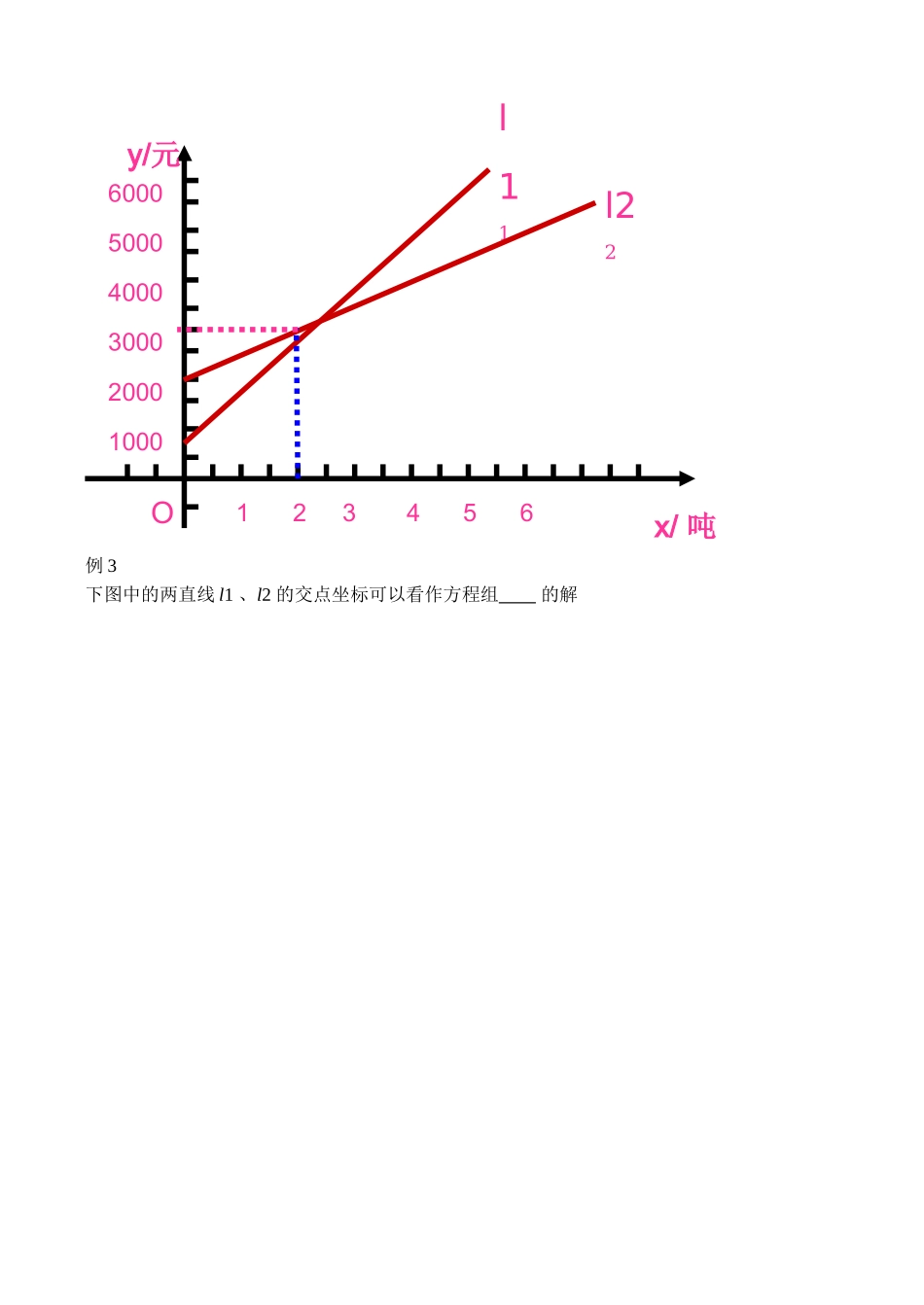
八年级数学二元一次方程组与一次函数教学目标知识要求:初步理解二元一次方程与一次函数的关系,能根据一次函数的图象求二元一次方程组的近似解.掌握运用二元一次方程和一次函数解决实际问题的方法.培养同学们分析问题、运用所学的知识解决实际问题的能力;体会对应关系和数形结合思想.教学重点:1.二元一次方程和一次函数的关系.2.能根据一次函数的图象求二元一次方程组的近似解.3.运用二元一次方程组和一次函数解决实际问题教学难点:方程和函数之间的对应关系即数形结合的意识和能力.教学过程:一.引入举例说明什么是二元一次方程?它的解个数如何?举出几组.看到x+y=5这个方程,同学们能联想到以前学过的哪些知识?这节课我们就一起来讨论他们之间的关系.二.讲授新课表示函数的方法还有哪些?下面请同学们画出一次函数的图象.思考问题:(1)以二元一次方程的解为坐标的点在一次函数图象上吗?(2)一次函数图象上的点的坐标都适合方程吗?(3)以方程的解为坐标的所有点组成的图象与一次函数的图象相同吗?在同一直角坐标系内分别作出一次函数y=5-x和y=2x-1的图像,这两个图像有交点吗?交点的坐标与方程组x+y=52x-y=1的解有什么关系?你能说明理由吗?[一次函数y=5-x和y=2x-1的图像的交点为(2,3),因此,x=2就是方程组y=3x+y=52x-y=1的解.]用作图象的方法解方程组x-2y=-22x–y=2解:由x-2y=-2可得y=,同理,由2x–y=2可得y=2x–2,在同坐标系中作出xyo1一次函数y=的图像和y=2x–2的图像,观察图像,得两直线交于点(2,2),所以方程组x-2y=-22x–y=2的解是x=2y=3解二元一次方程组除了代入法和加减法外还可以用图像法,那么用作图法来解方程组的步骤如下:1、把二元一次方程化成一次函数的形式2、在直角坐标系中画出两个一次函数的图像,并标出交点.3、交点坐标就是方程组的解.三.合作交流同一坐标系内作出两个函数图象,并列出相应的方程组,并比较、分析结果.得出方程组的解是相应两个函数图象交点的坐标.这样,我们又有了解方程组的新的方法——图象法,下面我们一起看一个例题.例1:利用图象解方程组y=2x-51-x=y例2:如图,l1反映了某公司产品的销售收入与销售量的关系,l2反映了该公司产品的销售成本与销售量的关系,当销售量为时,销售收入等于销售成本.例3下图中的两直线l1、l2的交点坐标可以看作方程组的解x/吨y/元O123456100040005000200030006000l11l22小结:用图象法解二元一次方程组的一般步骤:1.把两个方程都化成函数表达式的形式.2.画出两个函数的图象.3.找出交点坐标,交点坐标即为方程组的解.二元一次方程组无解<=>一次函数的图像平行(无交点)二元一次方程组有一解<=>一次函数的图像相交(有一个交点)二元一次方程组有无数个解<=>一次函数的图像重合(有无数个交点)作业:223344xx22-1-1yy00-1-11134