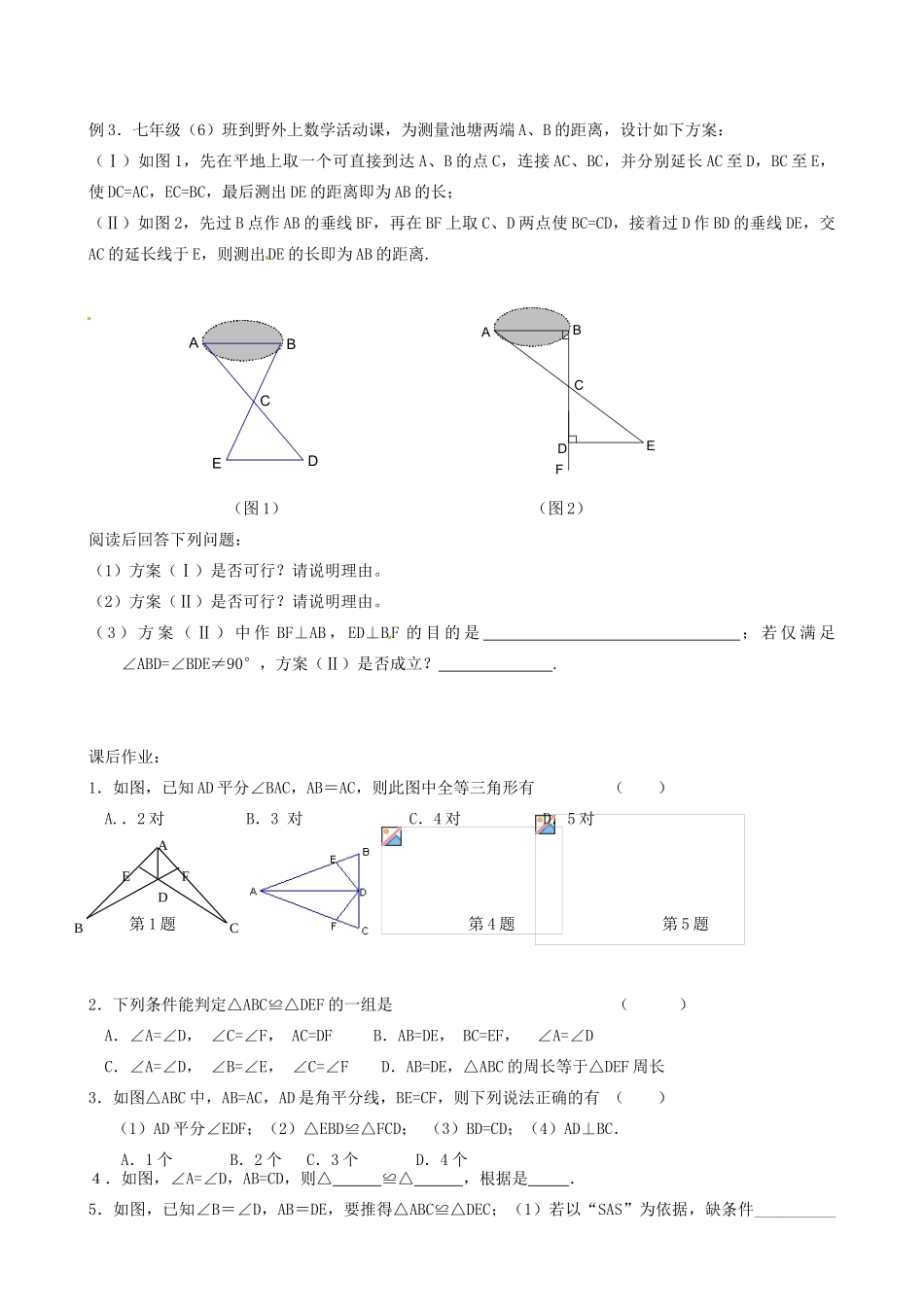
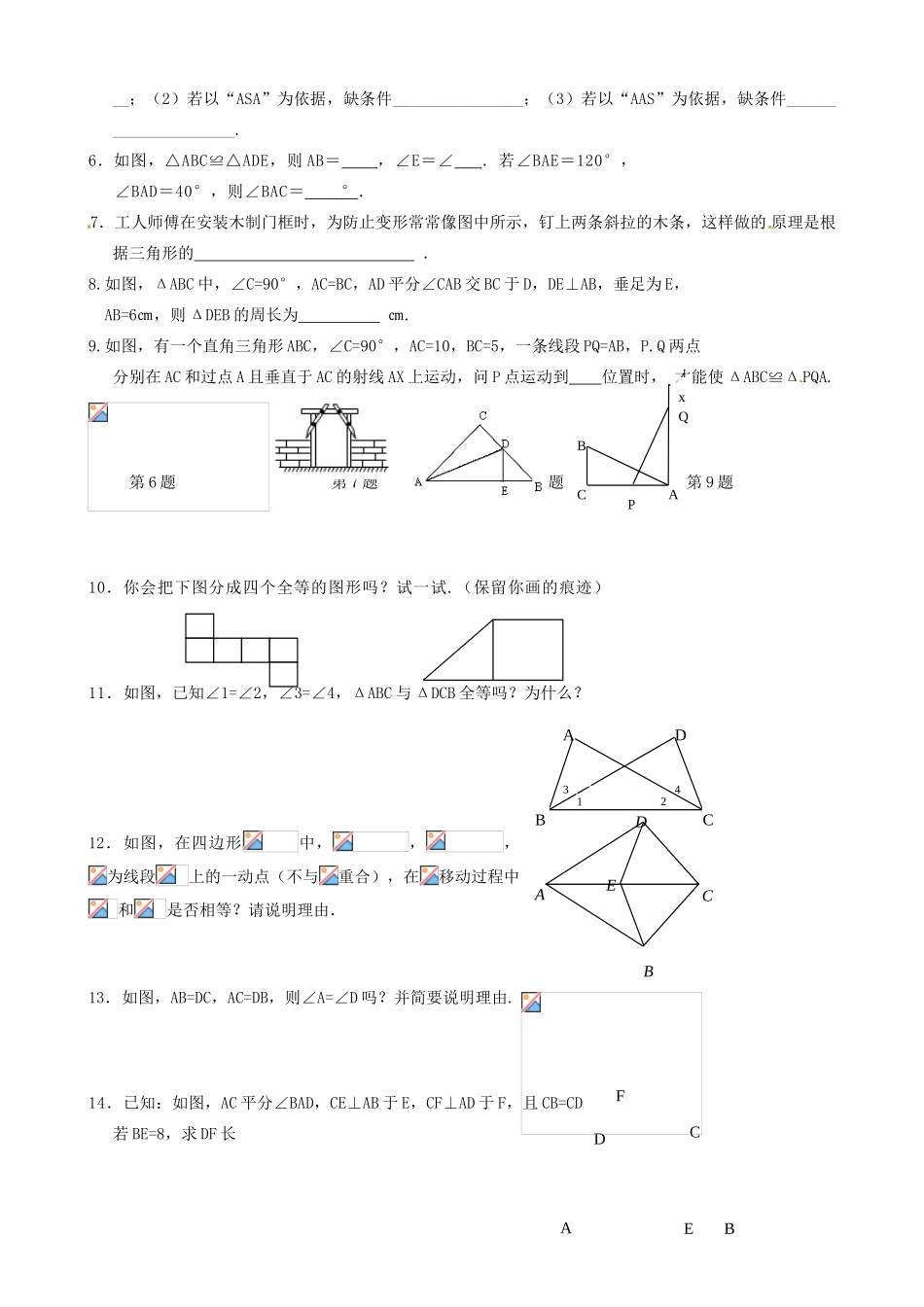
江苏省丹阳市华南实验学校七年级数学下册《全等三角形复习课》教案苏科版教学目标1.通过全等三角形的概念和识别方法的复习,让学生体会辨别、探寻、运用全等三角形的一般方法,体会主动实验,探究新知的方法;2.培养学生观察和理解能力,几何语言的叙述能力及运用全等知识解决实际问题的能力.重点:运用全等三角形的识别方法来解决实际问题.教学过程:回顾思考:1.全等三角形的定义:.2.全等三角形的性质:.3.一般三角形全等的判别方法:.直角三角形全等的判别方法:4.三个角对应相等的两个三角形全等吗?两边和其中一边的对角对应相等的两个三角形全等吗?试举反例说明.例题讲解:例1.等腰直角△ABC,其中AB=AC,∠BAC=90°,过B、C作经过A点直线L的垂线,垂足分别为M、N(1)你能找到一对三角形的全等吗?并说明.(2)BM,CN,MN之间有何关系?若将直线l旋转到如下图的位置,其他条件不变,那么上题的结论是否依旧成立?例2.已知:如图,在△ABC中.⑴分别以AB、AC为边向形外作正方形ABDE、ACFG.试说明:①CE=BG;②CE⊥BG;⑵分别以AB、AC为边向形外作正三角形△ABD、△ACE.试说明:①CD=BE;②求CD和BE所成的锐角的度数.例3.七年级(6)班到野外上数学活动课,为测量池塘两端A、B的距离,设计如下方案:(Ⅰ)如图1,先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB的长;(Ⅱ)如图2,先过B点作AB的垂线BF,再在BF上取C、D两点使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离.(图1)(图2)阅读后回答下列问题:(1)方案(Ⅰ)是否可行?请说明理由。(2)方案(Ⅱ)是否可行?请说明理由。(3)方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是;若仅满足∠ABD=∠BDE≠90°,方案(Ⅱ)是否成立?.课后作业:1.如图,已知AD平分∠BAC,AB=AC,则此图中全等三角形有()A..2对B.3对C.4对D.5对第1题第3题第4题第5题2.下列条件能判定△ABC≌△DEF的一组是()A.∠A=∠D,∠C=∠F,AC=DFB.AB=DE,BC=EF,∠A=∠DC.∠A=∠D,∠B=∠E,∠C=∠FD.AB=DE,△ABC的周长等于△DEF周长3.如图△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法正确的有()(1)AD平分∠EDF;(2)△EBD≌△FCD;(3)BD=CD;(4)AD⊥BC.A.1个B.2个C.3个D.4个4.如图,∠A=∠D,AB=CD,则△≌△,根据是.5.如图,已知∠B=∠D,AB=DE,要推得△ABC≌△DEC;(1)若以“SAS”为依据,缺条件__________EDCBAFEDCBAFEDABC__;(2)若以“ASA”为依据,缺条件________________;(3)若以“AAS”为依据,缺条件_____________________.6.如图,△ABC≌△ADE,则AB=,∠E=∠.若∠BAE=120°,∠BAD=40°,则∠BAC=°.7.工人师傅在安装木制门框时,为防止变形常常像图中所示,钉上两条斜拉的木条,这样做的原理是根据三角形的.8.如图,ΔABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB,垂足为E,AB=6㎝,则ΔDEB的周长为㎝.9.如图,有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P.Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到位置时,才能使ΔABC≌ΔPQA.第6题第7题第8题第9题10.你会把下图分成四个全等的图形吗?试一试.(保留你画的痕迹)11.如图,已知∠1=∠2,∠3=∠4,ΔABC与ΔDCB全等吗?为什么?12.如图,在四边形中,,,为线段上的一动点(不与重合),在移动过程中和是否相等?请说明理由.13.如图,AB=DC,AC=DB,则∠A=∠D吗?并简要说明理由.14.已知:如图,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且CB=CD若BE=8,求DF长DCAEBPQCABx4321ABCDABCDEF15.已知:如图,AB⊥BC,DC⊥BC,B、C分别是垂足。DE交AC于M,AC=DE,AB=EC,DE与AC有什么关系?请说明理由。16.阅读与证明:(4分)在一个三角形中,如果有两个角相等,那么这两个角所对的边也相等。如图①,在⊿ABC中,如果∠B=∠C,那么AB=AC。这一结论可以说明如下:解:过点A作AD⊥BC于D,则∠ADB=∠ADC=90º在⊿ABD与⊿ACD中图①∠B=∠C,∠ADB=∠ADC,AD=AD∴⊿A...