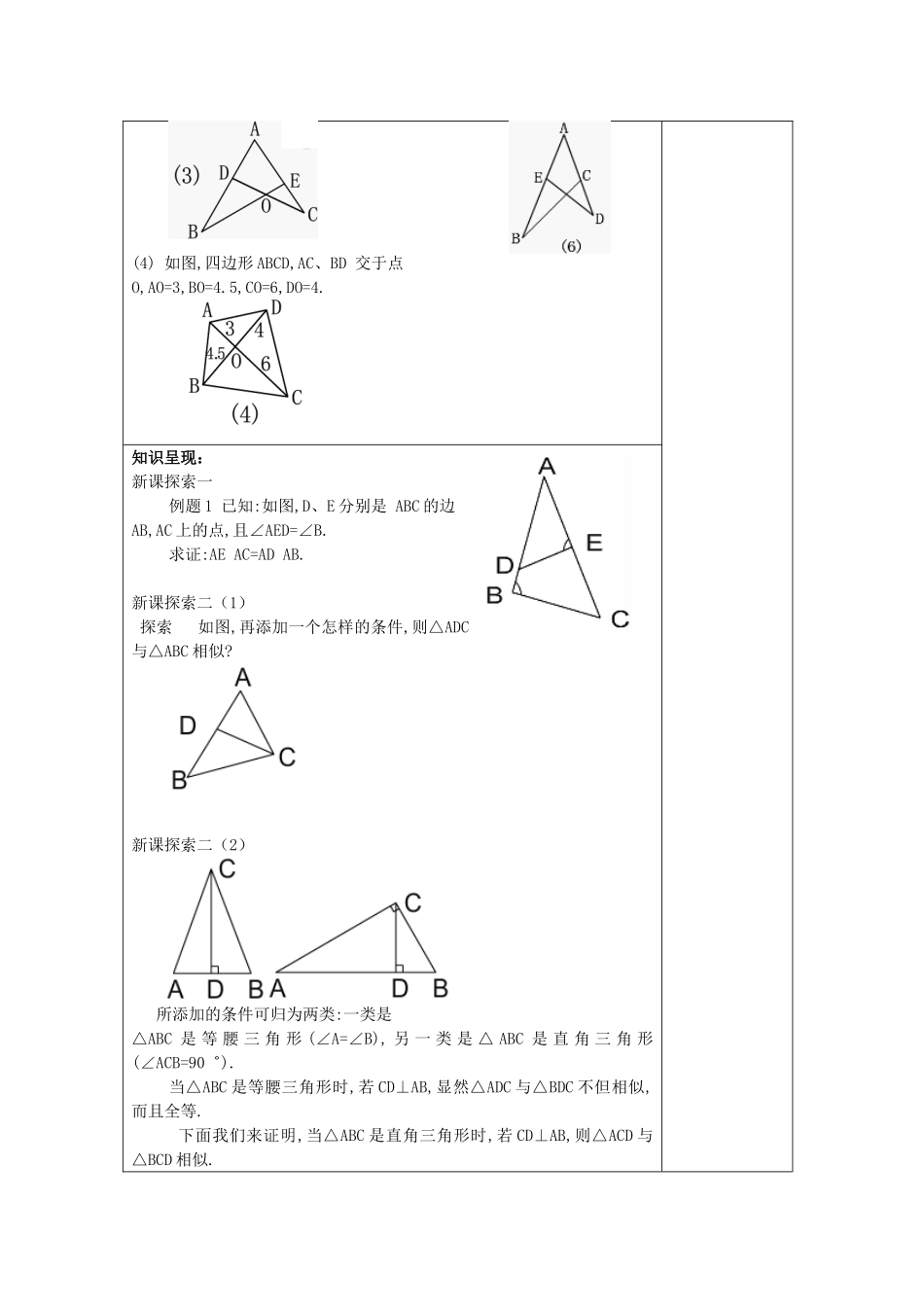
相似三角形的判定课题24.4(3)相似三角形的判定课型新授课教学目标熟练掌握相似三角形判定定理1、判定定理2、判定定理3.熟悉相似三角形中的基本图形.培养分类考虑的数学思想方法.重点熟练掌握相似三角形判定定理1、判定定理2、判定定理3难点应用判定定理教学准备相似三角形判定定理1、判定定理2、判定定理3等腰三角形的性质、直角三角形的性质学生活动形式讲练结合教学过程课题引入:课前练习一1.(1)有一个角是70゜的两个等腰三角形相似吗?(2)有一个角是110゜的两个等腰三角形相似吗?(3)顶角相等的两个等腰三角形相似吗?2.根据下列条件能否判定△ABC与△DEF相似?为什么?(1)∠B=40゜,∠C=65゜,∠D=75゜,∠F=40゜;(2)∠A=40゜,AB=20,AC=15,∠D=40゜,DE=4,EF=3;(3)∠B=72゜,AB=18,BC=15,∠F=72゜,EF=10,DF=12;(4)AB=12,BC=15,AC=24,DE=40,EF=20,FD=25.课前练习二3.根据下列各题的条件,分别说出图中相似的三角形:(1)如图,AD∥BC,AC、BD交于点O.(2)如图,∠BAD=∠C.(3)如图,∠B=∠C.备注:(4)如图,四边形ABCD,AC、BD交于点O,AO=3,BO=4.5,CO=6,DO=4.知识呈现:新课探索一例题1已知:如图,D、E分别是ABC的边AB,AC上的点,且∠AED=∠B.求证:AEAC=ADAB.新课探索二(1)探索如图,再添加一个怎样的条件,则△ADC与△ABC相似?新课探索二(2)所添加的条件可归为两类:一类是△ABC是等腰三角形(∠A=∠B),另一类是△ABC是直角三角形(∠ACB=90゜).当△ABC是等腰三角形时,若CD⊥AB,显然△ADC与△BDC不但相似,而且全等.下面我们来证明,当△ABC是直角三角形时,若CD⊥AB,则△ACD与△BCD相似.新课探索二(3)如图,Rt△ABC,CD是斜边上的高.求证:△ACD∽△CBD∽△ABC.新课探索三例题2已知:如图,点D是△ABC的边AB上的一点,且AD=4,BD=5,AC=6.求证:△ACD∽△ABC.新课探索四讨论在边长为1个单位的方格纸上,有格点(顶点在小方格的顶点上)三角形ABC与三角形FED.请问这两个三角形是否相似?若相似,请证明你的结论;若不相似,请说明理由.课内练习一1.已知:如图,∠1=∠2则图中有哪几对三角形相似?请证明你的结论.课内练习二2.一个三角形框架模型的边长分别为20厘米,30厘米,40厘米,木工要以一根长60厘米的木条为一边,做一个与模型相似的三角形.木工应该怎样选择其它两条边的长,才能使制作的三角形与模型三角形相似?三角形边长的选取方法可以有哪些?课内练习三3.如图是一个零件的剖面图,已知零件的外径为25毫米,为求出它的厚度x,需先求出内孔的直径AB,但不能直接量出AB.现用一个交叉卡钳(AC和BD的长相等)去量,若且量得CD长为7毫米.求零件的厚度x.课堂小结:1.进一步熟悉相似三角形的判定.2.利用相似三角形解决问题课外作业练习册预习要求24.4(4)相似三角形的判定课堂时间安排教师主导活动时间:20分钟学生主体活动时间:20分钟教学后记