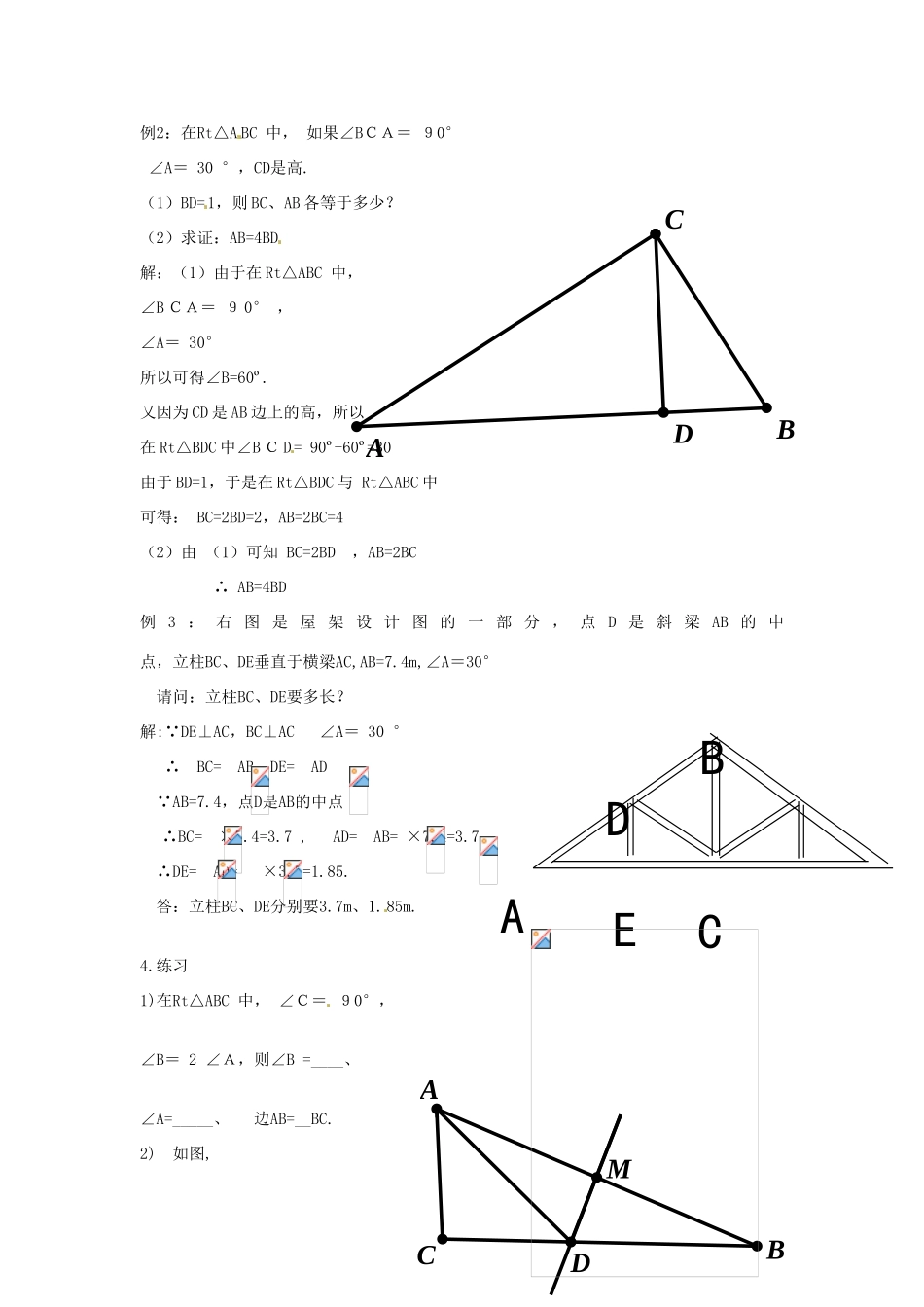
《12.3.2等边三角形(二)》教案学习目标:1.探索─发现─猜想─证明直角三角形中有一个角为30°的性质.2.有一个角为30°的直角三角形的性质的简单应用学习重点:含30°角的直角三角形的性质定理的发现与证明.学习难点:1.含30°角的直角三角形性质定理的探索与证明.2.全面、周到地思考问题.教学过程:1.复习回顾:等边三角形的判定及性质2.含30°的直角三角形性质探索在△ABD中,AB=BD=DA,AC是底边BD上的高,探究BC与AB之间的数量有什么关系?分析:∵AC是等边△ABD的高∴△ABD关于直线AC对称∴BC=CD∵AB=BD∴BC=CD=AB从而可得含30°的直角三角形性质定理:在一个直角三角形中,如果有一个角是30°,那么30°的角所对的直角边等于斜边的一半.引导学生从不同角度证明这一定理从而加深对定理的理解.3.例题例1:在Rt△ABC中,如果∠C=90°,∠A=30°,AB=4,求BC之长.解:∵在Rt△ABC中∠C=90°∠A=30°,AB=4∴BC=AB而AB=4∴BC=2ABDC例2:在Rt△ABC中,如果∠BCA=90°∠A=30°,CD是高.(1)BD=1,则BC、AB各等于多少?(2)求证:AB=4BD解:(1)由于在Rt△ABC中,∠BCA=90°,∠A=30°所以可得∠B=60º.又因为CD是AB边上的高,所以在Rt△BDC中∠BCD=90º-60º=30由于BD=1,于是在Rt△BDC与Rt△ABC中可得:BC=2BD=2,AB=2BC=4(2)由(1)可知BC=2BD,AB=2BC∴AB=4BD例3:右图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m,∠A=30°请问:立柱BC、DE要多长?解:∵DE⊥AC,BC⊥AC∠A=30°∴BC=AB,DE=AD∵AB=7.4,点D是AB的中点∴BC=×7.4=3.7,AD=AB=×7.4=3.7∴DE=AD=×3.7=1.85.答:立柱BC、DE分别要3.7m、1.85m.4.练习1)在Rt△ABC中,∠C=90°,∠B=2∠A,则∠B=____、∠A=_____、边AB=__BC.2)如图,BADCBADCEMACBD在△ABC中∠C=90°,∠B=15°,AB的垂直平分线交BC于D,交AB于M,且BD=8㎝,则AC=____.3)如图,在△ABC中,AB=AC,∠A=120°,AB的垂直平分线MN交BC于M,交AB于N,求证:CM=2BM证明:连结MA∵在△ABC中,AB=AC,∠BAC=120º∴∠B=∠C=30º∵MN是AB的垂直平分线∴MA=MB∴∠MAB=∠B=30º∴∠MAC=∠BAC-∠MAB=120º-30º=90º∴在Rt∆MAC中MC=2MA即CM=2BM5.小结含30°的直角三角形的性质定理:在一个直角三角形中,如果有一个角是30°,那么30°的角所对的直角边等于斜边的一半.6.作业布置:P/58(14)P/64(7)MNACB