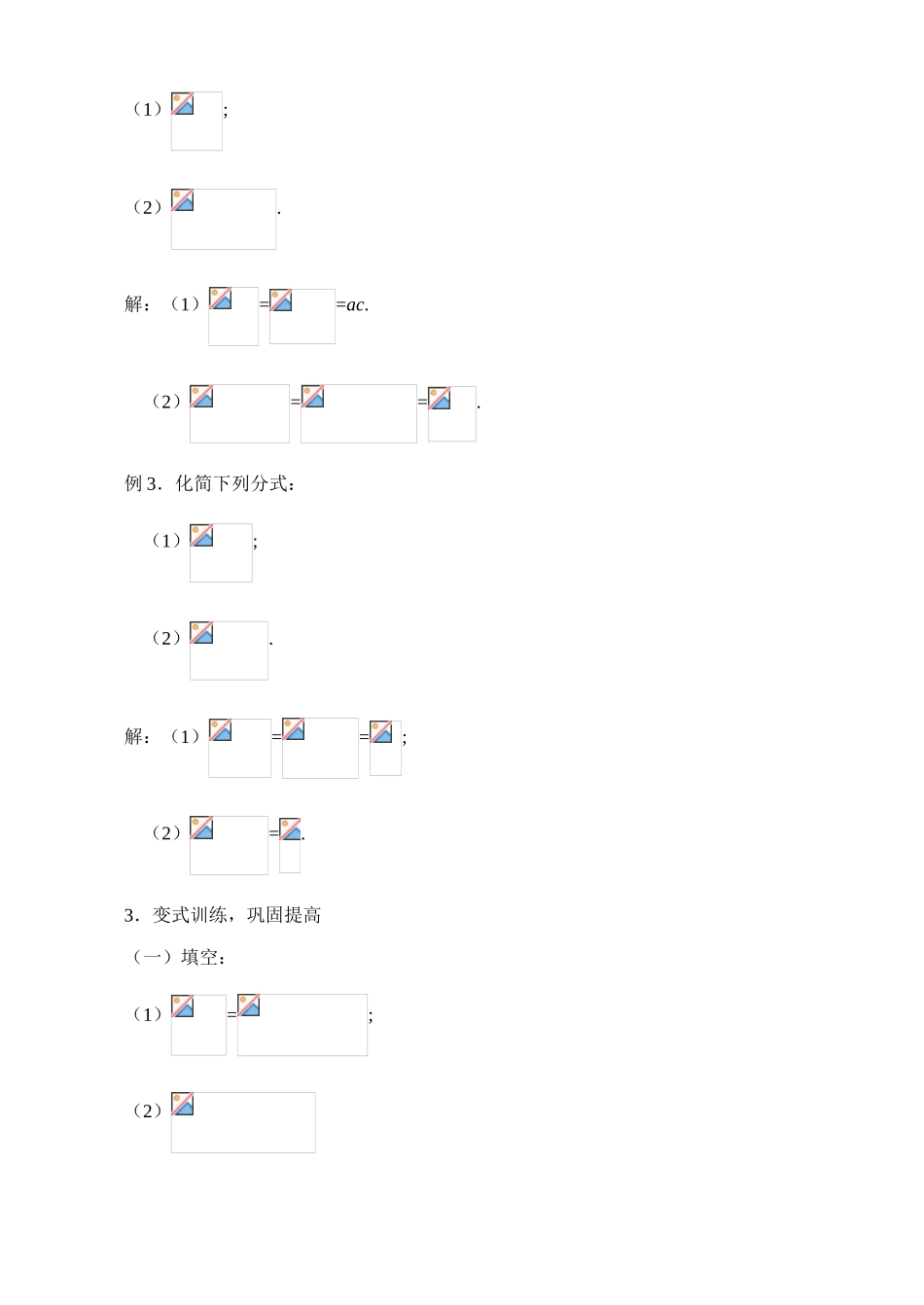
4.1(2)分式教学目标1.知识目标:掌握分式的基本性质;掌握分式约分的方法;了解最简分式的意义,能将分式化为最简分式.2.能力目标:类比分数的基本性质,推测出分式的基本性质,培养学生的类比思想.3.情感目标:通过类比分数的基本性质,类比出分式的基本性质,提高学生学数学的兴趣.教学重点会将一个分式化简为最简分式.教学难点复杂分式的约分.教学方法类比教学法教学过程1.创设情境,自然引入计算:+.+=+=+=.这里将异分母化为同分母,==,==.这里根据分数的基本性质:分数的分子与分母都乘以(或除以)同一个不等于零的数,分数的值不变.2.设问质疑,探究尝试利用分数的基本性质,是否可以推想分式的性质呢?(1)=的依据是什么?将的分子、分母同时除以它们的最大公约数3得到.即==.依据是分数的基本性质:分数的分子与分母同除以同一个不等于零的数,分数的值不变.(2)分式与相等吗?分式与相等,在分式中,a≠0,所以==;(3)分式与相等吗?分式与相等.在分式中,n≠0,所以==.由此,我们能推想出分式的基本性质:分式的分子与分母都乘以(或除以)同一个不为零的整式,分式的值不变.在运用此性质时,应特别注意:分式的分子、分母都乘以(或除以)同一个不为零的整式中的“都”“同一个”“不为零”。例1.下列等式的右边是怎样从左边得到的?(1)=(y≠0);(2)=.解:(1)==;(2)==.例2.化简下列各式:(1);(2).解:(1)==ac.(2)==.例3.化简下列分式:(1);(2).解:(1)==;(2)=.3.变式训练,巩固提高(一)填空:(1)=;(2)答案:(1)因为==所以括号里应填2x2+2xy;(2)因为==.所以括号里应填y-2.(二)化简下列分式:(1);(2).(3)(4)答案:(1);(2).(3)(4)(三)已知=2,求的值.答案:4.总结串联,纳入系统理解了分式的意义;分式的基本性质及约分的意义;会利用分式的基本性质进行分式的化简与变形及化简分式时,结果一定要求最简.教学检测一、请你选一选1.下列变形不正确的是()A.B.(x≠1)C.=D.2.下列分式中,当x=-2时,有意义的是()A.B.C.D.3.等式成立的条件是()A.a≠0且b≠0B.a≠1且b≠1C.a≠-1且b≠-1D.a、b为任意数4.如果把分式中的x和y都扩大10倍,那么分式的值()A.扩大10倍B.缩小10倍C.是原来的D.不变5.不论x取何值时,下列分式总有意义的是()A.B.C.D.6.若x2-9=0,则分式的值为()A.1B.-5C.1或-5D.5二、请你填一填1.代数式中,是整式的有________,是分式的有________.2.若M=,则当x______时,M有意义;当x=____时,M=0;当x=____时,M=4.3.当x________时,分式的值为正数.4.等式成立的条件是________.5.将分式的分子、分母中各项系数都化为整数,且分式的值不变,那么变形后的分式为________________.6.若2x=-y,则分式的值为________.三、请你来解答1.化简下列分式(1)(2)(3)(4)2.化简求值:其中x=2,y=3.3.已知,求的值.4.已知x=,求的值参考答案一、请你选一选1.C2.B3.C4.D5.D6.B二、请你填一填1.-2.≠±123.<54.a≠±15.6.三、请你来解答1.(1)-(2)-(3)(4)2.-3.4.解:由已知x=,得2x=+1,2x-1=.所以(2x-1)2=5,x2-x-1=0即x2=x+1.我们利用x2=x+1可以使降次从而求出它的值.=======.