立体几何的共线共点共面问的题目教师版VIP免费

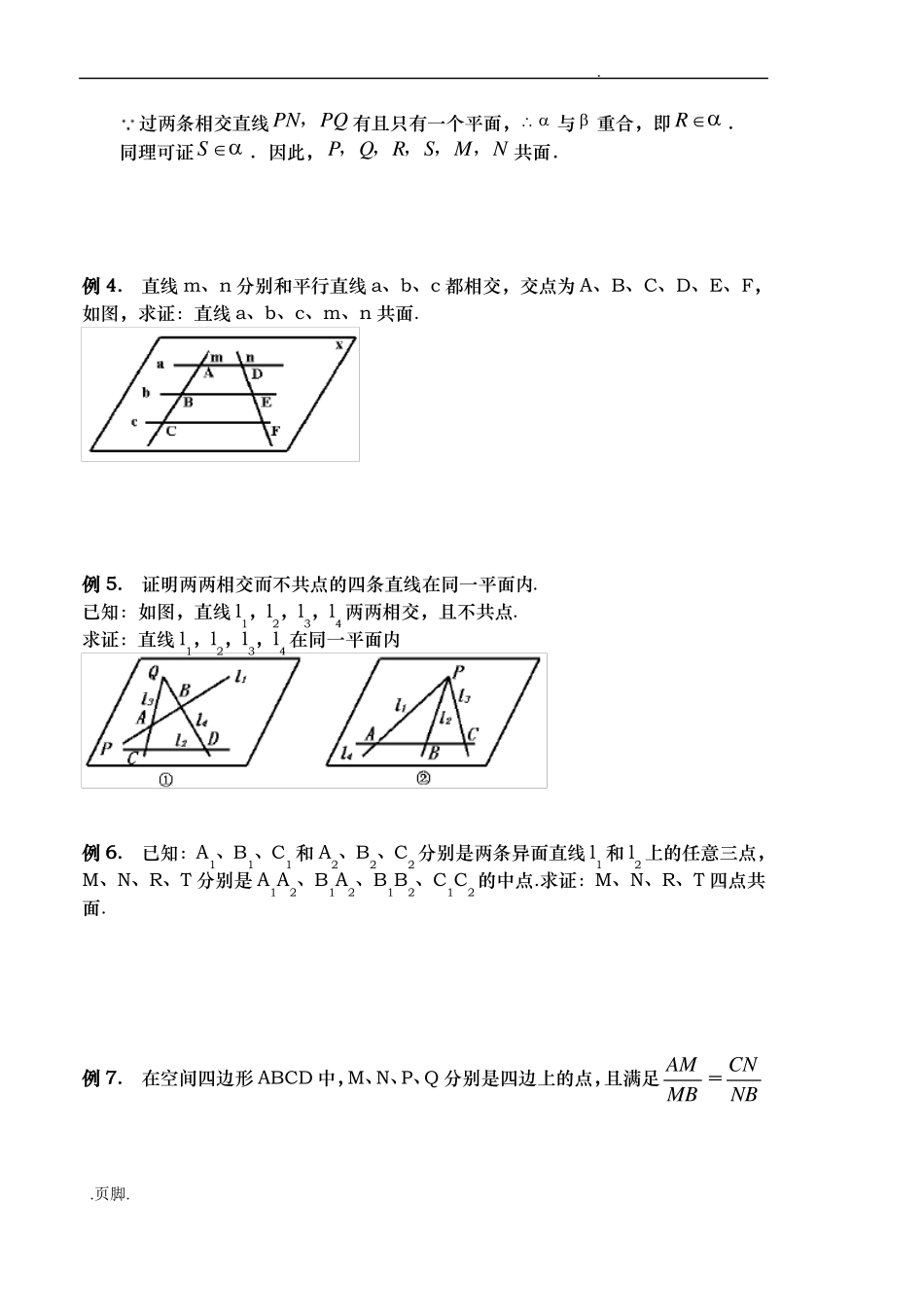
.立体几何中的共点、共线、共面问题一、共线问题例1.若ΔABC所在的平面和ΔA1B1C1所在平面相交，并且直线AA1、BB1、CC1相交于一点O，求证：(1)AB和A1B1、BC和B1C1、AC和A1C1分别在同一平面内；(2)如果AB和A1B1、BC和B1C1、AC和A1C1分别相交，那么交点在同一直线上(如图).例2.点P、Q、R分别在三棱锥A-BCD的三条侧棱上，且PQ∩BC＝X,QR∩CD＝Z,PR∩BD＝Y.求证：X、Y、Z三点共线.例3.已知△ABC三边所在直线分别与平面α交于P、Q、R三点，求证：P、Q、R三点共线。1．如图1，正方体ABCDA1B1C1D1中，A1C与截面DBC1交O点，AC，BD交M点，求证：C1，O，M三点共线．证明：连结A1C1，又C1平面A1ACC1，且C1平面DBC1，C1是平面A1ACC1与平面DBC1的公共点．MAC，M平面A1ACC1．MBD，M平面DBC1．M也是平面A1ACC1与平面DBC1的公共点．.页脚..C1M是平面A1ACC1与平面DBC1的交线．O为A1C与截面DBC1的交点，O平面A1ACC1，O平面DBC1，即O也是两平面的公共点．∴OC1M，即C1，M，O三点共线．2．如图，在四边形ABCD中，已知AB∥CD，直线AB，BC，AD，DC分别与平面α相交于点E，G，H，F．求证：E，F，G，H四点必定共线（在同一条直线上）．分析：先确定一个平面，然后证明相关直线在这个平面内，最后证明四点共线．证明 AB//CD，AB，CD确定一个平面β．又 AB∩α＝E，ABβ，Eα，Eβ，即E为平面α与β的一个公共点．同理可证F，G，H均为平面α与β的公共点． 两个平面有公共点，它们有且只有一条通过公共点的公共直线，∴E，F，G，H四点必定共线．点评：在立体几何的问题中，证明若干点共线时，先证明这些点都是某两平面的公共点，而后得出这些点都在二平面的交线上的结论．二、共面问题1.如图3，设P，Q，R，S，M，N分别为正方体ABCDA1B1C1D1的棱AB，BC，CC1，C1D1，A1D1，A1A的中点，求证：P，Q，R，S，M，N共面．证明：如图3，连结A1B，MQ，NR．P，N分别为AB，A1A的中点，A1B∥PN．A1D1∥BC，A1M∥BQ．M，Q分别为A1D1，BC的中点，四边形A1BQM为平行四边形．A1B∥MQ．PN∥MQ．因此，直线PN，MQ可确定一个平面．同理，由PQ∥NR可知，直线PQ，NR确定一个平面．A1MBQ．.页脚..过两条相交直线PN，PQ有且只有一个平面，与重合，即R．同理可证S．因此，P，Q，R，S，M，N共面．例4.直线m、n分别和平行直线a、b、c都相交，交点为A、B、C、D、E、F，如图，求证：直线a、b、c、m、n共面.例5.证明两两相交而不共点的四条直线在同一平面内.已知：如图，直线l1，l2，l3，l4两两相交，且不共点.求证：直线l1，l2，l3，l4在同一平面内例6.已知：A1、B1、C1和A2、B2、C2分别是两条异面直线l1和l2上的任意三点，M、N、R、T分别是A1A2、B1A2、B1B2、C1C2的中点.求证：M、N、R、T四点共面.例7.在空间四边形ABCD中，M、N、P、Q分别是四边上的点，且满足AMCN＝MBNB.页脚..＝AQCP＝＝k.QDPD(1)求证：M、N、P、Q共面.(2)当对角线AC＝a,BD＝b，且MNPQ是正方形时，求AC、BD所成的角及k的值(用a,b表示)三、共点问题例8.三个平面两两相交得三条直线，求证：这三条直线相交于同一点或两两平行.1.如图2，已知空间四边形ABCD，E，F分别是AB，AD的中点，G，H分别是BC，CD上的点，且BGDH2，求证：EG，FH，AC相交于同一点P．GCHC1错解：证明：E、F分别是AB,AD的中点,EF∥BD,EF=2BD,1BGDH又GCHC2,GH∥BD,GH=3BD,四边形EFGH是梯形，设两腰EG,FH相交于一点T,DHHC2,F分别是AD.AC与FH交于一点.直线EG,FH,AC相交于一点正解：证明：E，F分别是AB，AD的中点，1BGDH2，EF∥BD，且EFBD．又2GCHC1GH∥BD，且GHBD．EF∥GH，且EFGH．3四边形EFHG是梯形，其两腰必相交，设两腰EG，FH相交于一点P， EG平面ABC，FH平面ACD，P平面ABC，P平面ACD，PAC．又平面ABC平面ACDAC，故EG，FH，AC相交于同一点P．2.如图，已知平面α，β，且α∩β＝l．设梯形ABCD中，AD∥BC，且ABα，CDβ，求证：AB，CD，共点（相交于一点）．.页脚.l.分析：AB，CD是梯形ABCD的两条腰，必定相交于一点M，只要证明M在l上，而l是两个平面α，β的交...