对数函数的图像和性质教学设计VIP免费

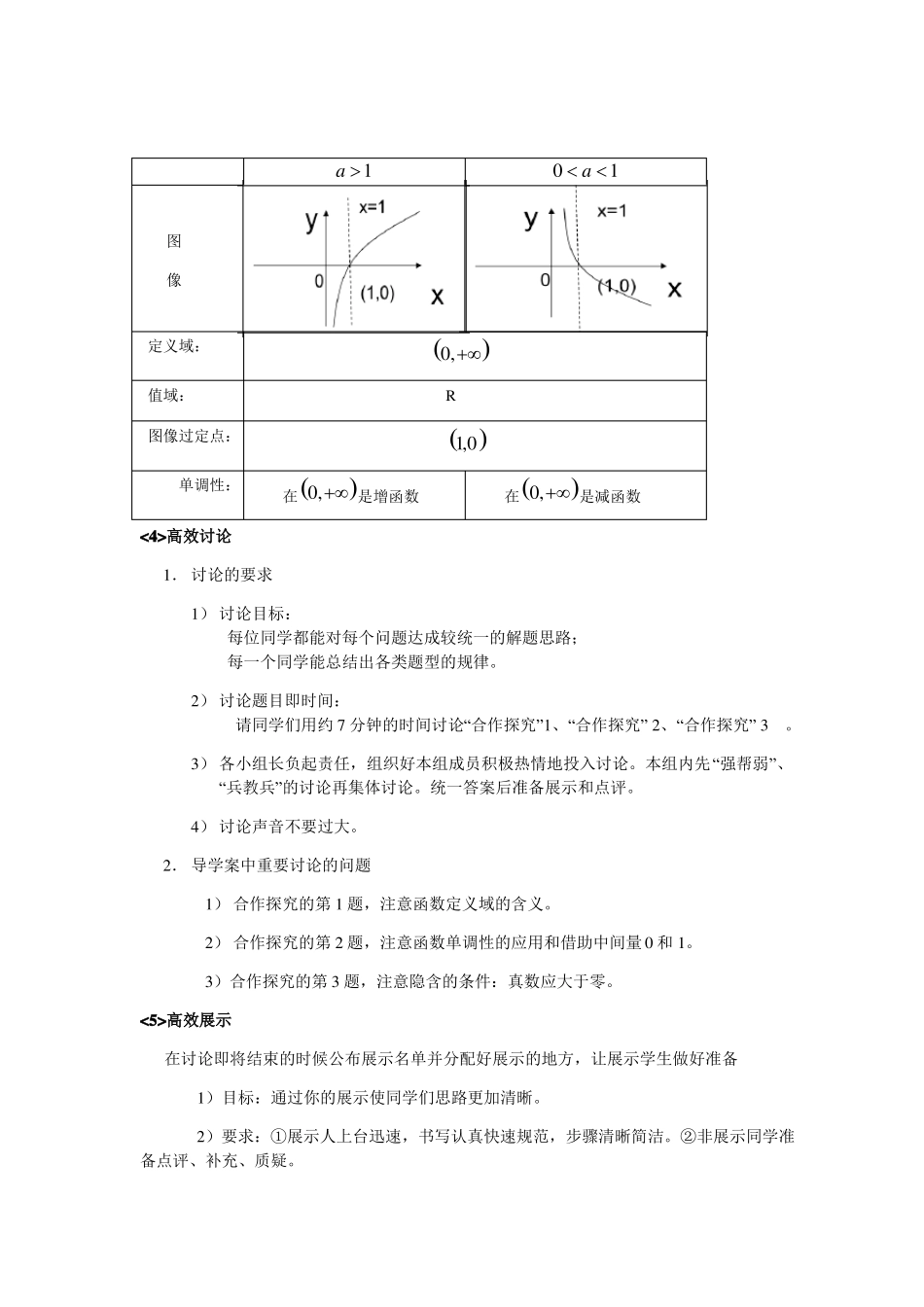
对数函数的图像和性质一、教学内容分析：1、对数是学生在高一刚刚接触到的新概念，不易理解，计算的形式具有一定的复杂性.2、以对数作为基础的对数函数是高中函数学生最不易掌握的函数类型。3、函数是高中十分重要的概念.其中关于定义域、值域、单调性、奇偶性、对称性等函数的性质应有一个整体的理解，这在学习、解决函数问题的过程中显得十分重要，应在适当的时机对学生这种函数的整体观点加以培养，这节课的学习过程是一个能够把握的机会。二、学生分析：1、学生从初中到高一年级接触到了一些函数和研究函数的一些方法。2、学生在前面学习了指数函数，知道指数函数和对数函数的关系，能够类比指数函数的研究方法来研究对数函数的图像和性质。3、学生能够选择描点作图的方法来研究对数函数的图像与性质，也能够通过研究指数函数反函数的方法来研究对数函数的图像和性质等。三、教学目标：1、会画对数函数的图像，理解对数函数的性质。2、对于函数的性质与函数图像的形态之间的关系有一个初步的整体的理解，体会研究函数性质的过程中数形结合、分类讨论归纳的数学思想方法在研究问题过程中的体现。3、培养学生对问题实行质疑的意识，培养学生在学习的过程中交流的习惯。四、教学重点：对数函数的图像和性质。五、教学难点：对数函数的图像和性质的应用。六、教学活动：<1>.复习导入新课复习对数函数的概念定义：一般的，我们把形如ylogax（a0，且a1）的函数叫做对数函数，其中x是自变量。定义域为(0,)，值域为R。分析对数函数和指数函数的关系，它们互为反函数，能够类似指数函数的研究方法来研究对数函数，复习指数函数的图像及性质。引出课题——对数函数的图像和性质<2>.目标解读知识与技能：掌握对数函数的图像，并能通过图像研究对数函数的性质，并能解决求函数定义域、比较大小、解不等式等。过程与方法：充分利用数形结合以及类比指数函数的性质，探究、总结对数函数的性质；由特殊的对数函数的图像和性质推广到一般的对数函数的图像和性质。情感、态度、价值观：通过对比指数函数和对数函数图像与性质，体会数学的美妙之处，激发学习数学的兴趣。<2>学案反馈1．反馈导学案的完成情况，表扬优秀小组、优秀个人、进步个人、认真细致个人。2．分析导学案中存有的态度方面及知识方面的问题。<3>知识梳理完成问题导学1画出函数ylog2x和ylog1x的图象2列表x14-2212-1110021-142-2ylog2xylog1x21．展台展示优秀的作图，强调作图的步骤：列表、描点、连线。分析对数函数和指数函数互为反函数的关系，它们的图像关于直线y=x对称，能够先画出指数函数的图象，然后将其关于直线y=x对称，便可得到对应的对数函数的图象。2．对问题导学1中对数函数的底数分析，2>1，0<1<1，将其拓展到一般情况a1和20a1中去，让学生体会从特殊到一般的研究方法，画出对数函数的一般式ylogax(a0,a1)中，a1和0a1两种情况对应的函数图象。接着让一个学生引导同学们完成问题导学2的表格，分析函数的定义域、值域、恒过点，以及函数在a1和0a1时对应的不同单调性。3．分析对数函数图象与直线x=1的关系，在a1时，01,y>0;在0a1时，00;x>1,y<0;a10a1图像定义域：值域：图像过定点：单调性：<4>高效讨论1．讨论的要求1）讨论目标：每位同学都能对每个问题达成较统一的解题思路；每一个同学能总结出各类题型的规律。2）讨论题目即时间：请同学们用约7分钟的时间讨论“合作探究”1、“合作探究”2、“合作探究”3。3）各小组长负起责任，组织好本组成员积极热情地投入讨论。本组内先“强帮弱”、“兵教兵”的讨论再集体讨论。统一答案后准备展示和点评。4）讨论声音不要过大。2．导学案中重要讨论的问题1）合作探究的第1题，注意函数定义域的含义。2）合作探究的第2题，注意函数单调性的应用和借助中间量0和1。3）合作探究的第3题，注意隐含的条件：真数应大于零。<5>高效展示在讨论即将结束的时候公布展示名单并分配好展示的地方，让展示学生做好准备1）目标：通过你的展示使同学们思路更加清晰。2）要求：①展示人上台迅速，书写认真快速...