真题试卷武昌区2022022学年八上期末数学试题-版可编辑可直接打印-含答案VIP免费

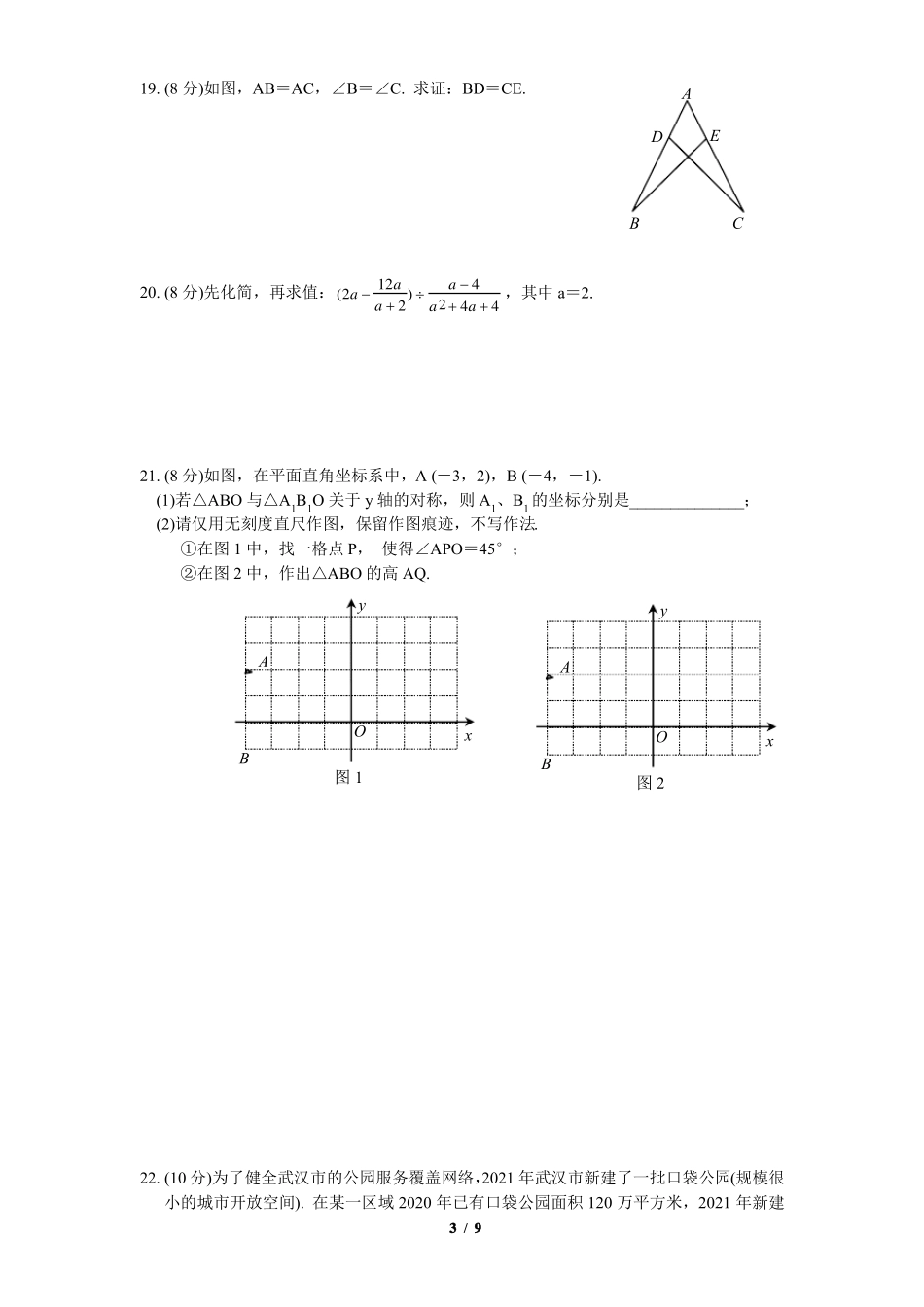
武昌区2021-2022学年度素养调研八年级数学试题一、选择题(每小题3分，共30分)1.北京2022年冬奥会会微如右图，组成会微的四个图案中的图形是轴对称图形的是（）A.2．若代数式B.C.D.x在实数范围内有意义，则实数x的取值范围是（）1xA.x＝0B.x≠－1C.x＝1D.x≠13.一种微粒的半径是0.00002米，数0.00002用科学记数法表示为（）－－－A.2×105B.0.2×104C.2×103D.2×1054．下列运算正确的是（）A.x2·x3＝x6B.(2x)3＝6x3C.(－x2)3＝－x6D.2xy2＋3yx2＝5xy2E5.如图，点E、H、G、N共线，∠E＝∠N，EF＝NM，添加一个条件，H不能判断△EFGO△NMH的是（）A.EH＝NGB.∠F＝∠MC.FG＝MHD.FG∥HMFG6.计算21的结果是（）x24x22xMNA.x2x2x2B.C.D.x2x2x2x(x2)7.将下列多项式分解因式，结果中不含有因式(x＋2)的是（）A.x2＋2xB.x2－4C.(x－2)2＋8(x－2)＋16D.x3＋3x2－4x8.在等腰△ABC中，AB＝AC＝3，BC＝3，∠A＝120°，点D在边BC上.若△ABD是直角三角形，则AD的长度是（）A.33333B.或1C.或D.1或222229.在平面直角坐标系中，已知点A(－1，1)，B(－3，2)，点C在坐标轴上，若△ABC是等腰三角形，则满足条件的点C的个数是（）A.4个B.5个C.7个D.8个A10.如图，△ABC中，点D在BC上，∠ACB＝75°，∠BAC＝∠ADC＝60°，AE⊥BC于E，CF⊥AD于F，AE、CF相交于点G.DC＝m，AF＝n，则线段EG的长为（）FG11111111A.nmB.nmC.nmD.nmBDEC242224221/9二、填空题(每小题3分，共18分)11.若分式x2的值为0，则x的值是________.1x12.若一个n边形的内角和等于1980°，则边数n＝_______.13.若(x＋6)(x＋8)＝x2＋mx＋48，则m＝_________.14.如图，在△ABC中，AB的垂直平分线交BC于M，AC的垂直平分线交BC于N，连接AM、AN，若∠MAN＝10°，则∠BAC＝_______°.AMNCB15.已知x－3y＝1，x3－3x2y－7xy＋9y2＝－3，则xy的值是_________.16.如图，在△ABC中，∠ACB＝2α，CD平分∠ACB，∠CAD＝30°－α，∠BAD＝30°，则∠BDC＝__________.(用含α的式子表示)ADBC三、解答题(共8小题，共72分)17.(8分)(1)计算：(a－1)(a＋2)；(2)因式分解：4xy2－4xy＋x.18.(8分)解分式方程：(1)2/93x131.；(2)2xx2x93x19.(8分)如图，AB＝AC，∠B＝∠C.求证：BD＝CE.20.(8分)先化简，再求值：(2a12aa4)2，其中a＝2.a2a4a4ADEBC21.(8分)如图，在平面直角坐标系中，A(－3，2)，B(－4，－1).(1)若△ABO与△A1B1O关于y轴的对称，则A1、B1的坐标分别是______________；(2)请仅用无刻度直尺作图，保留作图痕迹，不写作法.①在图1中，找一格点P，使得∠APO＝45°；②在图2中，作出△ABO的高AQ.yyAAOxOxBB图1图222.(10分)为了健全武汉市的公园服务覆盖网络，2021年武汉市新建了一批口袋公园(规模很小的城市开放空间).在某一区域2020年已有口袋公园面积120万平方米，2021年新建3/9口袋公园34万平方米，人均口袋公园面积比2020年增加了2平方米，人口增加了10%，请回答下列问题：(1)求2020年该区域人口为多少万人?(2)每个口袋公园面积平均为5万平方米，预计2022年该区域人口比2021年再增加10%，为了达到人均口袋公园面积比2021年再增加1平方米的目标，至少应新建多少个口袋公园?23.(10分)如图1，在△ABC中，BE平分∠ABC，CF平分∠ACB，BE与CF交于点D.(1)若∠BAC＝74°，则∠BDC＝_______；(2)如图2，∠BAC＝90°，作MD⊥BE交AB于点M，求证：DM＝DE；(3)如图3，∠BAC＝60°，∠ABC＝80°，若点G为CD的中点，点M在直线BC上，连接MG，将线段GM绕点G逆时针旋转90°得GN，NG＝MG，连接DN，当DN最A短时，直接写出∠MGC的度数.AAEMFDEFFEGDDCBMNBCCB图2图3图124.(12分)在平面直角坐标系中，点A在x轴的负半轴上，点B在y轴的正半轴上，点A与点C关于y轴对称.(1)如图1，OA＝OB，AF平分∠BAC交BC于F，BE⊥AF交AC于E，请直接写出EF与EC的数量关系为______________；(2)如图2，AF平分∠BAC交BC于F，若AF＝2OB，求∠ABC的度数；4/9(3)如图3，OA＝OB，点G在BO的垂直平分线上，作∠GOH＝45°交BA的延长线于H，连接GH，试探究OG与GH的数量和位置关系.AyBFyBFGDO图1ECxAO图2CxHA图3OxyB武昌区2021-2022学年度素养调研八年级数学试题参考答案5/96/97/98/99/9