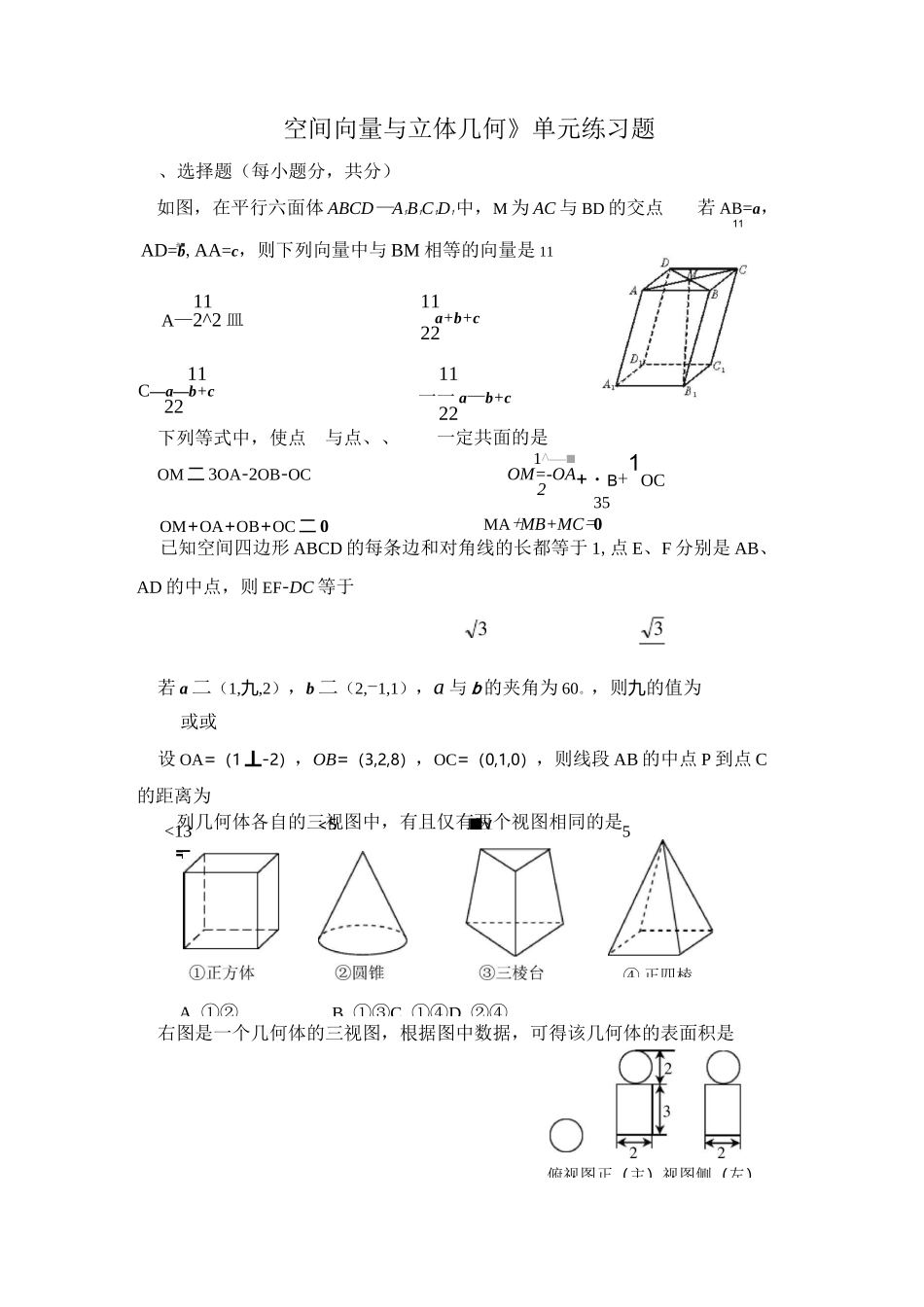
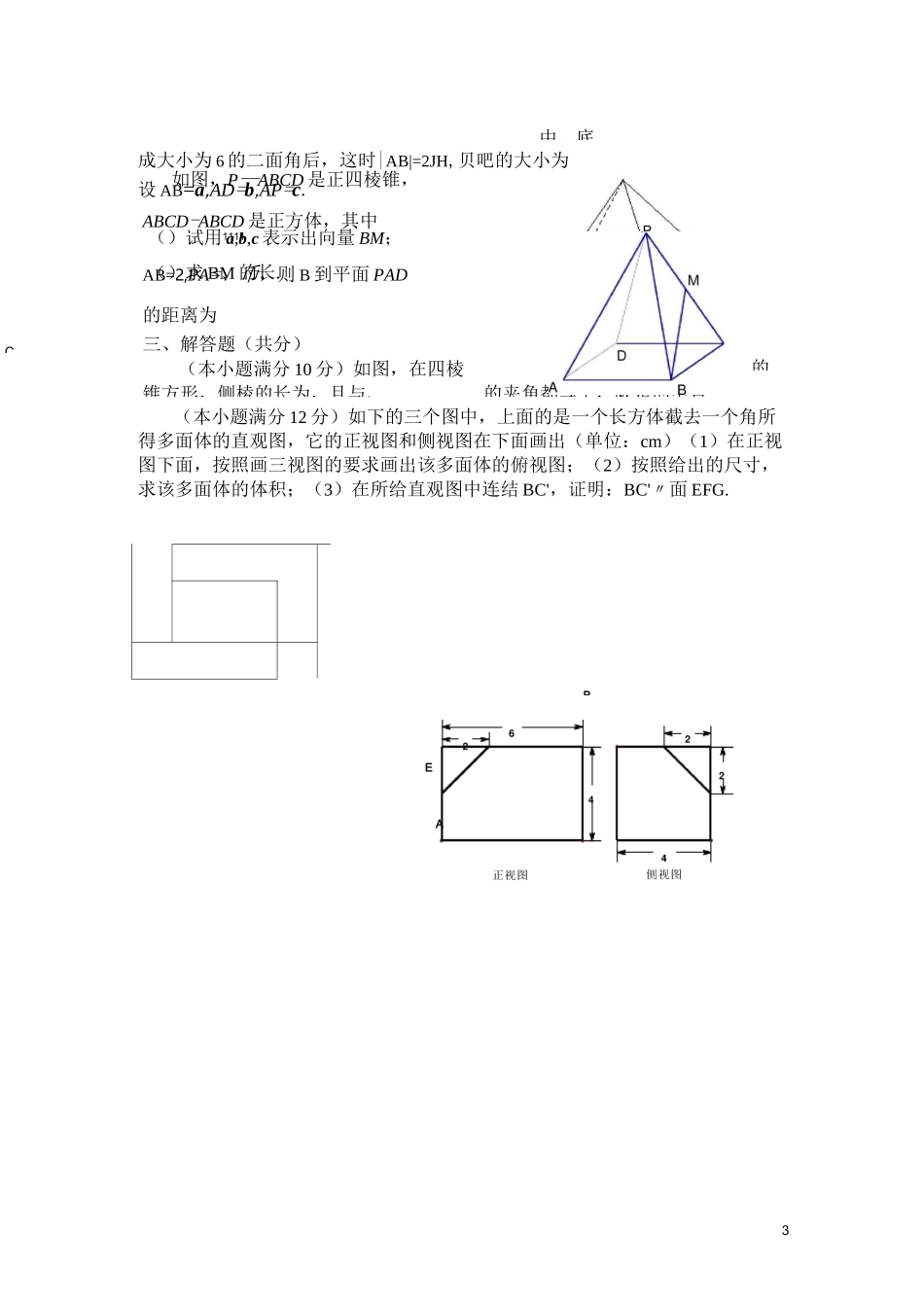
<13〒<5■v53TA.①②B.①③C.①④D.②④已知空间四边形ABCD的每条边和对角线的长都等于1,点E、F分别是AB、AD的中点,则EF-DC等于若a二(1,九,2),b二(2,-1,1),a与b的夹角为60。,则九的值为或或设OA=(1丄-2),OB=(3,2,8),OC=(0,1,0),则线段AB的中点P到点C的距离为列几何体各自的三视图中,有且仅有两个视图相同的是右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是④正四棱空间向量与立体几何》单元练习题俯视图正(主)视图侧(左)、选择题(每小题分,共分)如图,在平行六面体ABCD—A1B1C1D1中,M为AC与BD的交点若AB=a,11上■AD=b,AA=c,则下列向量中与BM相等的向量是1111A—2^2皿11a+b+c2211C—a—b+c2211一一a—b+c22下列等式中,使点OM二3OA-2OB-OC与点、、一定共面的是1^―■OM=-OA2+・B+1OC35OM+OA+OB+OC二0MA+MB+MC=02B10nC11nD12n如图,ABCD-A1B1C1D1为正方体,下面结论错误的是ABD〃平面CB"]BAC丄BDCAC]丄平面CB]D]D异面直线AD与CB]所成的角为60°如图,在长方体ABCD-A]B]C]D]中,AB=BC=2,AA]=1,贝VBC与平面BB]D]D所成角的正弦值为A色B三C西D西3555/的三个顶点分别是A(l,—1,2),B(5,—6,2),C(1,3,—1),J贝边上的高长为2、污中,为的中点,则点到平面.设,,是空间三条直线,a,p是空间两个平面,则下列命题中,逆命题不成立的是.当丄a时,若丄p,则a〃p.当ua时,若丄p,则a丄p.当ua,且是在a内的射影时,若丄,贝U丄.当ua,且Qa时,若〃a,贝V〃二、填空题(每小题分,共分)设a二(x,4,3),b二(3,—2,y),且a//b,则xy=已知向量a=(0,—1,1),b=(4,1,0),\ka+b\=Q9且九〉0,则九=在直角坐标系xOy中,设(,),(,),沿x轴把直角坐标平面折如图,P—ABCD是正四棱锥,ABCD-ABCD是正方体,其中1111AB=2,PA=、币,则B到平面PAD的距离为三、解答题(共分)(本小题满分10分)如图,在四棱锥方形,侧棱的长为,且与、中,底BiCi的的夹角都等于,M是的中点,3成大小为6的二面角后,这时|AB|=2JH,贝吧的大小为设AB=a,AD=b,AP=c.()试用a,b,c表示出向量BM;()求BM的长.(本小题满分12分)如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm)(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;(2)按照给出的尺寸,求该多面体的体积;(3)在所给直观图中连结BC',证明:BC'〃面EFG.PCBEA面角E-AF-C的余弦值.4(本小题满分12分)如图,在四面体ABCD中,CB=CD,AD丄BD,点E,F分别是AB,BD的中点.求证:(1)直线EF//面ACD;(2)平面EFC丄面BCD.(本小题满分12分)如图,已知点P在正方体ABCD-AB'C'D'的对角线BD'上,Z°()求DP与CC'所成角的大小;()求DP与平面AA'D'D所成角的大小(本小题满分12分)已知一四棱锥P-ABCD的三视图如下,E是侧棱PC上的动点.(1)求四棱锥P-ABCD的体积;(2)是否不论点E在何位置,都有BD丄AE?证明你的结论;(3)若点E为PC的中点,求二面角D-AE-B的大小.(本小题满分12分)如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA丄平面ABCD,ZABC=60。,E,F分别是BC,PC的中点.()证明:AE丄PD;()若H为PD上的动点,EH与平面pAD所成最大角的正切值为岁,求二ACCABEC一、选择题BDDDD10由A=AB|[COS
=AB-=4,所以|AC|=BDAB—AD故AB「=(AC+CD+DB)2=AC+CD2+|DB「+2(AC-CD+CD-DB+DB-AC)•••BA=(—2,0,2),1三、解答题)所求多面体体积#=V长方体-1三棱锥=4x4x6—_x3284(cm2).5空间向量与立体几何》单元练习题参考答案二、填空题9作丄轴于,丄轴于,则AB=AC+CD+DB]I,II,I*!I*11\,・■!AC=3,CD=5,pB=2,AC-CD=0,CD-DB=0,AC-DB=AC-DBCOS(180O—0)=—6COS0,_1・・・(2d1)2=32+52+22+2(0—0—6COS0),.・.COS0=——•由于OO<0<18OO,AO=12OO2*以A1B1为x轴,A1D1为y轴,A1A为z轴建立空间直角坐标系设平面PAD的法向量是m=(x,y,z),>>>•/AD=(0,2,0),AP=(1,1,2),・:y=0,x+y+2z=0,取z=1得m=(—2,0,1),|BA-m・•・B至【」平面PAD的距离d=一1mpM卜f,•・・BM的长为f解:()如图()证明:在长方体ABCD—A,B,CD中,连结AD,,则AD,〃BC'.因为E,G分别为AA',A'D'中点,所以AD'〃EG,从而EG〃B...