2022年中考数学反比例函数综合强化训练VIP免费

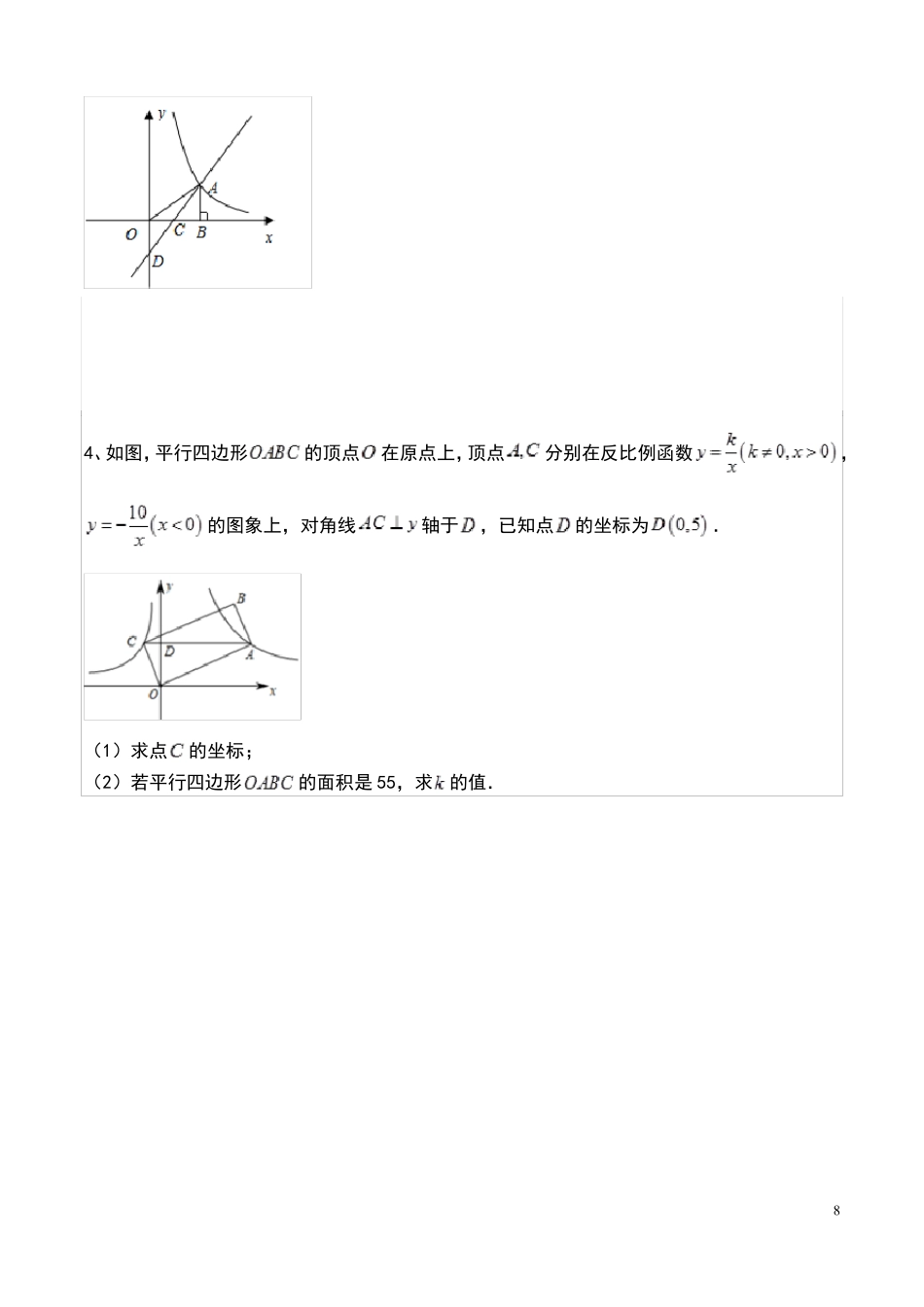
2022年中考数学：反比例函数综合强化训练1、如图，一次函数y=-x+1的图象与反比例函数y=的图象分别交于点A、B，且点A的横坐标为-2，点B的横坐标为4，一次函数的图象与y轴交于点C.（1）求反比例函数的表达式；（2）若点P在y轴上，且△ABP的面积为6，求出点P的坐标。12kx2、如图，一次函数y＝﹣x+1的图象与两坐标轴分别交于A，B两点，与反比例函数的图象交于点C（﹣2，m）．（1）求反比例函数的解析式；（2）若点P在y轴正半轴上，且与点B，C构成以BC为腰的等腰三角形，请直接写出所有符合条件的P点坐标．3、如图所示，在直角坐标系中，点A是反比例函数y1k的图象上一点，ABx轴的正半轴于xB点，C是OB的中点；一次函数y2axb的图象经过A、C两点，并将y轴于点D0，若2，（1）求反比例函数和一次函数的解析式；（2）观察图象，指出在y轴的右侧，当y1y2时x的取值范围．S△AOD4．14、如图，平行四边形的顶点在原点上，顶点分别在反比例函数，的图象上，对角线轴于，已知点的坐标为．（1）求点的坐标；的面积是55，求的值．（2）若平行四边形85、如图，在平面直角坐标系xOy中，一次函数的图象与反比例函数y＝（k＜0）的图象在第二象限交于A（﹣3，m），B（n，2）两点．（1）当m＝1时，求一次函数的解析式；（2）若点E在x轴上，满足∠AEB＝90°，且AE＝2﹣m，求反比例函数的解析式．6、如图所示，一次函数y＝mx+n（m≠0）的图象与反比例函数y=𝑘（k≠0）的图象交于第二、四象限的点A（﹣2，a）和点B（b，﹣1），过A点作x轴的垂线，垂足为点C，△AOC的面积为4．（1）分别求出a和b的值；（2）结合图象直接写出mx+n＞𝑘中x的取值范围；（3）在y轴上取点P，使PB﹣PA取得最大值时，求出点P的坐标．𝑘𝑘97、如图，一次函数的图象y＝ax+b（a≠0）与反比例函数y＝（k≠0）的图象交于点A（，4），点B（m，1）．（1）求这两个函数的表达式；（2）若一次函数图象与y轴交于点C，点D为点C关于原点O的对称点，点P是反比例函数图象上的一点，当S△OCP：S△BCD＝1：3时，请直接写出点P的坐标．8、如图，在平面直角坐标系中，一次函数y＝mx+n（m≠0）的图象与y轴交于点C，与反比例函数y＝（k≠0）的图象交于A，B两点，点A在第一象限，纵坐标为4，点B在第三象限，BM⊥x轴，垂足为点M，BM＝OM＝2．（1）求反比例函数和一次函数的解析式．（2）连接OB，MC，求四边形MBOC的面积．109、如图，已知直线y1＝x+m与x轴、y轴分别交于点A，B，与双曲线y2＝（x＜0）分别交于点C，D，且点C的坐标为（﹣1，4）．（1）分别求直线、双曲线的函数表达式；（2）求点D的坐标；（3）利用函数图象直接写出：当x在什么范围内取值时y2＜y1．10、如图，一次函数y1＝ax+b与反比例函数y2＝的图象相交于A（2，8），B（8，2）两点，连接AO，BO，延长AO交反比例函数图象于点C．（1）求一次函数y1的表达式与反比例函数y2的表达式；（2）当y1＜y2，时，直接写出自变量x的取值范围为；（3）点P是x轴上一点，当S△PAC＝S△AOB时，请直接写出点P的坐标为．1111、如图，已知A(4，n)，B(2，4)是一次函数ykxb的图象和反比例函数y交点．(1)求反比例函数和一次函数的解析式；(2)求直线AB与x轴的交点C的坐标及△AOB的面积；(3)求方程kxbm0的解（请直接写出答案）；xm的图象的两个x(4)求不等式kxbm0的解集（请直接写出答案）.x12、如图，在平面直角坐标xOy中，正比例函数y＝kx的图象与反比例函数y＝的图象都经过点A（2，﹣2）．（1）分别求这两个函数的表达式；（2）将直线OA向上平移3个单位长度后与y轴交于点B，与反比例函数图象在第四象限内的交点为C，连接AB，AC，求△ABC的面积；（3）在（2）的条件下，反比例函数y＝的图象上是否存在点D，使CD⊥BC？若存在，请直接写出点D的坐标；若不存在，请说明理由．、1213、已知，在直角坐标系中，平行四边形OABC的顶点A，C坐标分别为A（2，0），C（﹣1，2），反比例函数y＝的图象经过点B（m≠0）（1）求出反比例函数的解析式（2）将OABC沿着x轴翻折，点C落在点D处，作出点D并判断点D是否在反比例函数y＝的图象上（3）在x轴是否存在一点P使△OCP为等腰三角形？若存在，写...