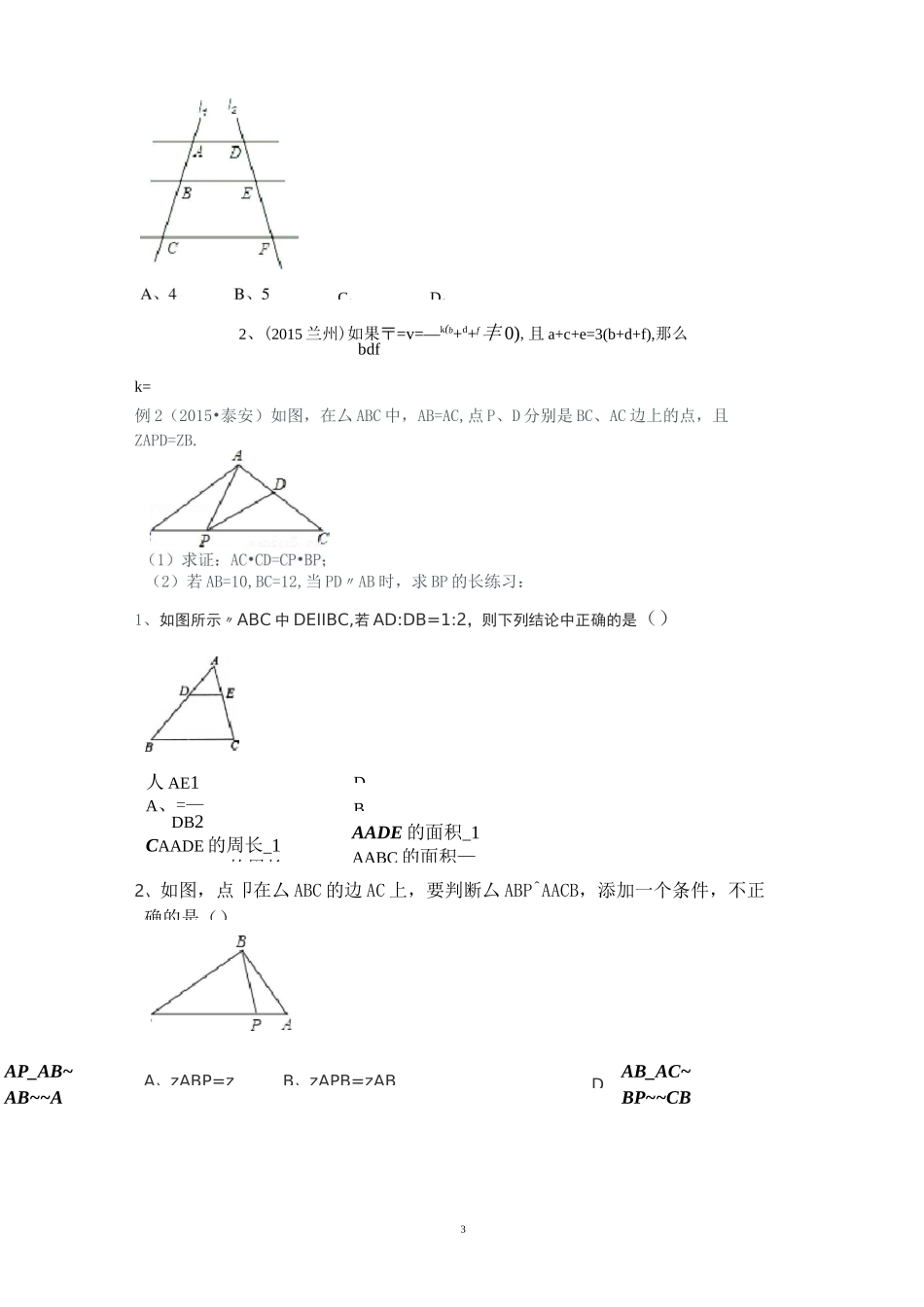
1相似三角形复习课教学设计【教学目标】知识与技能:1.复习相似三角形的概念。2.复习相似三角形的性质。3.复习相似三角形的判定。4.复习相似三角形的应用,用相似知识解决一些数学问题。过程与方法:在梳理全等三角形与相似三角形知识的过程中,感受类比思想,划归思想;情感态度与价值观:总结图形相似的有关特征并应用到实际问题的解决中,培养应用数学的能力。【重点难点】重点:运用相似三角形的判定定理分析两个三角形是否相似。难点:正确运用相似三角形的性质解决数学问题。【课型】复习课【教学过程】同学们:今天这节课我们来复习相似三角形的有关内容,请同学们想一想,我们在相似三角形方面学习了哪些内容。考点1比例线段及平行线分线段成比例定理1、比例线段ac对于四条线段a、b、c、d,如果其中两条线段的比等于另两条线段的比,如〒=亏(或bd写作a:b),我们就说这四条线段成比例线段,简称比例线段。ac2、比例的基本性质:若丁,则ab=bc.bd3、平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其它直线上截得的线段也相等。平行于三角形一边的直线截其他两边或两边的延长线),所得的对应线段成比例。考点2相似三角形的性质与判定。1、相似三角形的性质(1)对应边成比例、对应角相等.(2)相似三角形的对应高、中线、和角平分线的比等于相似比,相似三角形的周长的比等于相似比,相似三角形面积的比等于相似比的平方。2、相似三角形的判定定理(1)位置判定法:平行于三角形一边的直线和其他两边或其延长线相交,所得的三角形与原三角形相似;(2)边角关系判定法:①斜边的比等于一线直角边的比的两个直角三角形相似。②三边对应成比例的两个三角形相似;③两角对应相等的两个三角形相似;④两边对应成比例且夹角相等的两个三角形相似。考点3相似三角形性质的实际应用在实际生活中,处处都存在相似三角形,当我们与其接触时,就能利用相似的相关知识去识别和解决相关实际生活中的问题,如2①同一时刻物高与影长的问题;②利用相似测量无法直接测量的物体③利用相似进行图形设计等运用相似的知识解决一些实际问题,要能够在理解题意的基础上,把它转化为纯数学知识的问题,要注意培养数学建模的思想。考点41、位似图形的定义:如果两个多边形不仅相似,而且对应顶点的连线交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫作位似中心。(1)位似图形一定是相似图形,但相似图形不一定是位似图形;(2)两个位似图形的位似中心只有一个(3)相似三角形的对应边的比、周长比、对应高的比、对应中线的比、对应角平分线的比都等于相似比,但面积的比等于相似比的平方。2、位似变换:在平面直角坐标中,如果位似变换是以原点为位似中习,相似比为k,那么位似图形对应点的坐标的比等于k或-k。(浙江舟山)如图,直线l〃l〃l,直线AC分别交l,l,l于点A,123123B,C;直线DF分别交l,l,l于点D,E,F.AC与DF相交于点G,123DE且AG=2,GB=1,BC=5,则了丁的值为()123A、_B2C_D-255练习:y3x+y1、(2015东营)或一=丁,贝y的值为()x4x457A、1B、_C、_D、_7442、(2015•眉山)如图,AD〃BE〃CF,直线11、12与这三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则EF的长为()3C、D、人AE1A、=—DB2CAADE的周长_1、AABC的周长DBAADE的面积_1AABC的面积—A、zABP=zB、zAPB=zABAP_AB~AB~~ADAB_AC~BP~~CB2、(2015兰州)如果〒=v=—k(b+d+f丰0),且a+c+e=3(b+d+f),那么bdfk=例2(2015•泰安)如图,在厶ABC中,AB=AC,点P、D分别是BC、AC边上的点,且ZAPD=ZB.(2)若AB=10,BC=12,当PD〃AB时,求BP的长练习:1、如图所示〃ABC中DEIIBC,若AD:DB=1:2,则下列结论中正确的是()2、如图,点卩在厶ABC的边AC上,要判断厶ABP^AACB,添加一个条件,不正确的是()43、如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF丄AM,垂足为F,交AD的延长线于点E,交DC于点N.(1)求证:△ABMs^EFA;2)若AB=12,BM=5,求DE的长.(2014•牡丹江)在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上...