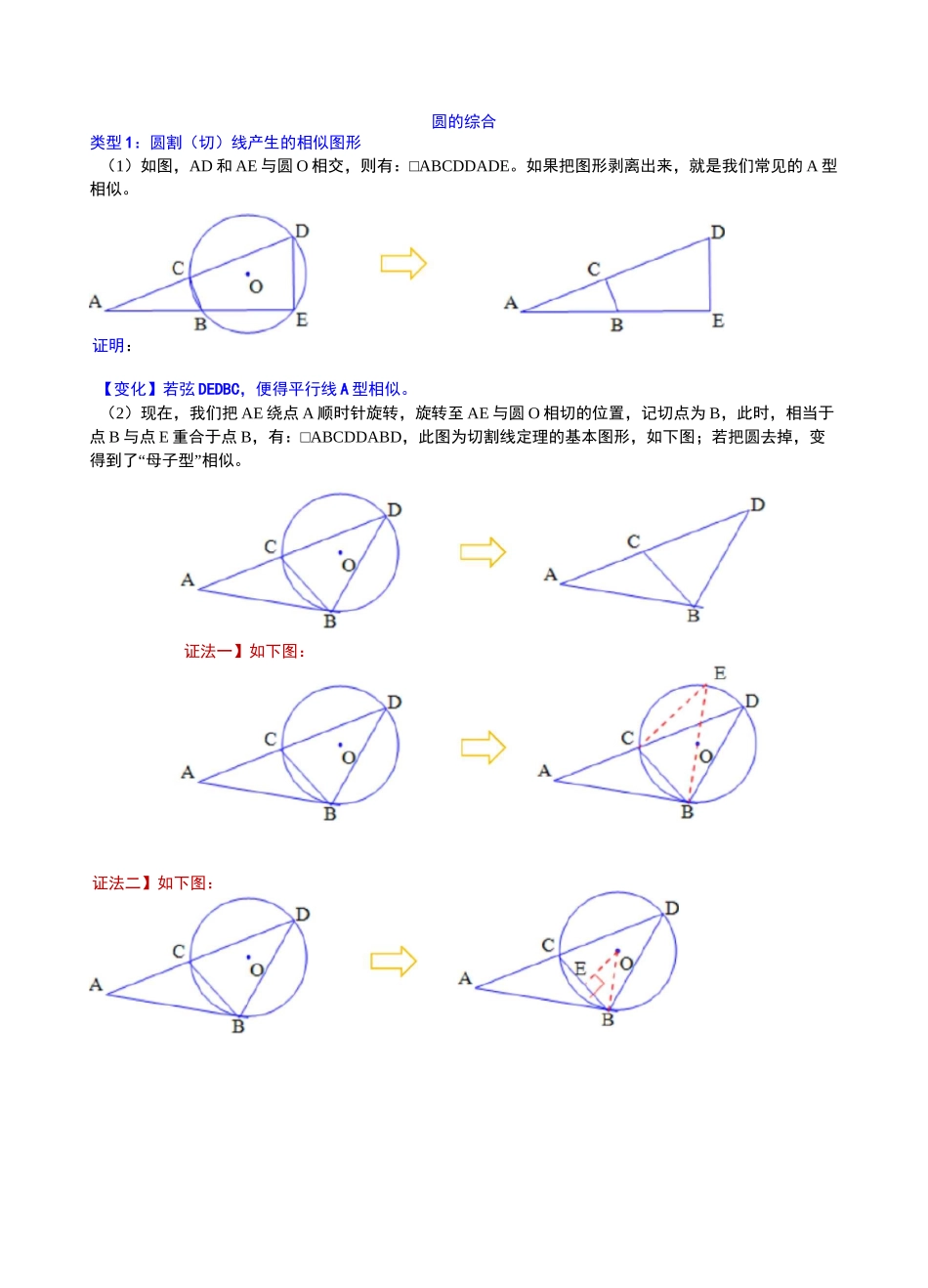
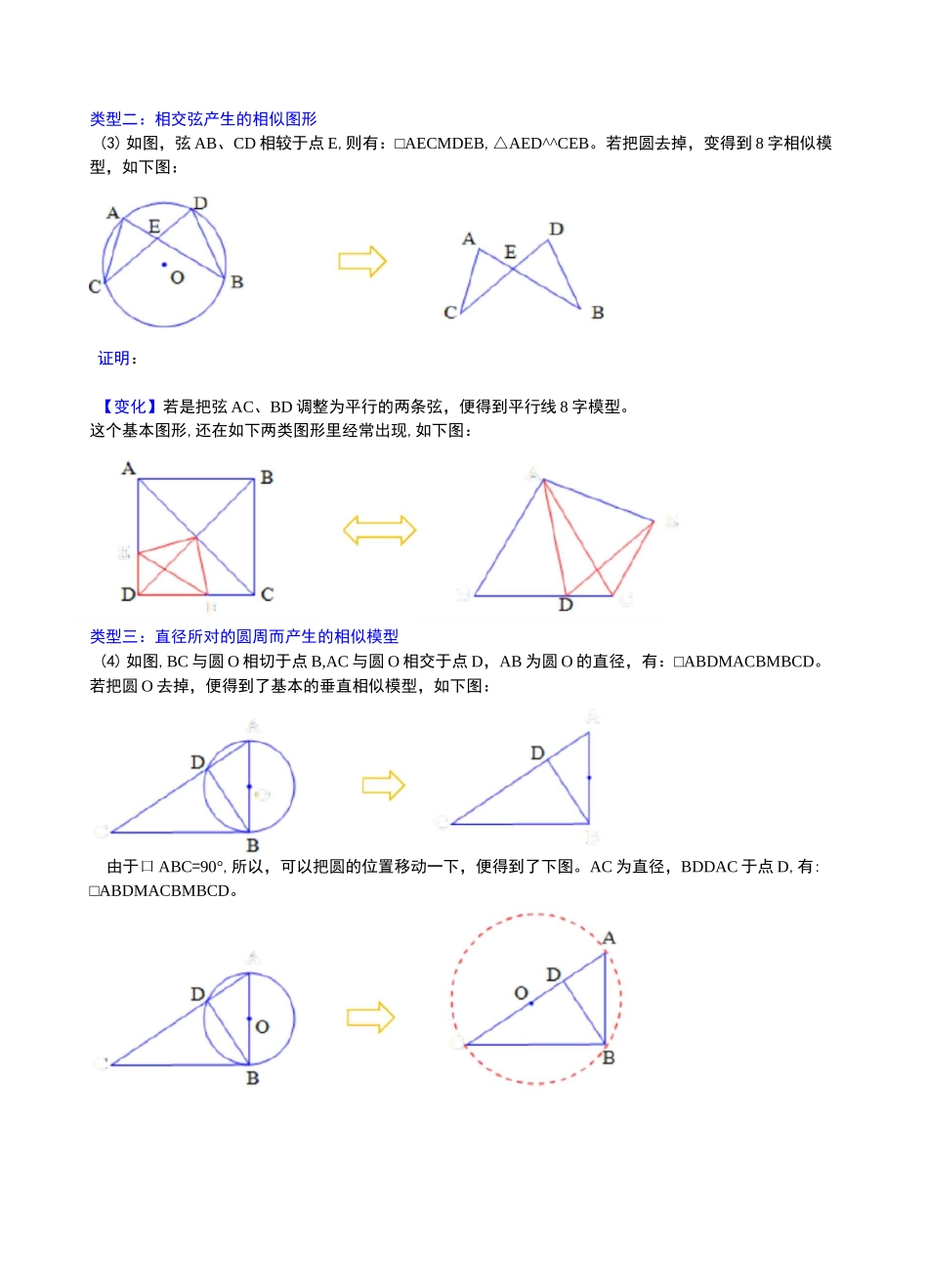
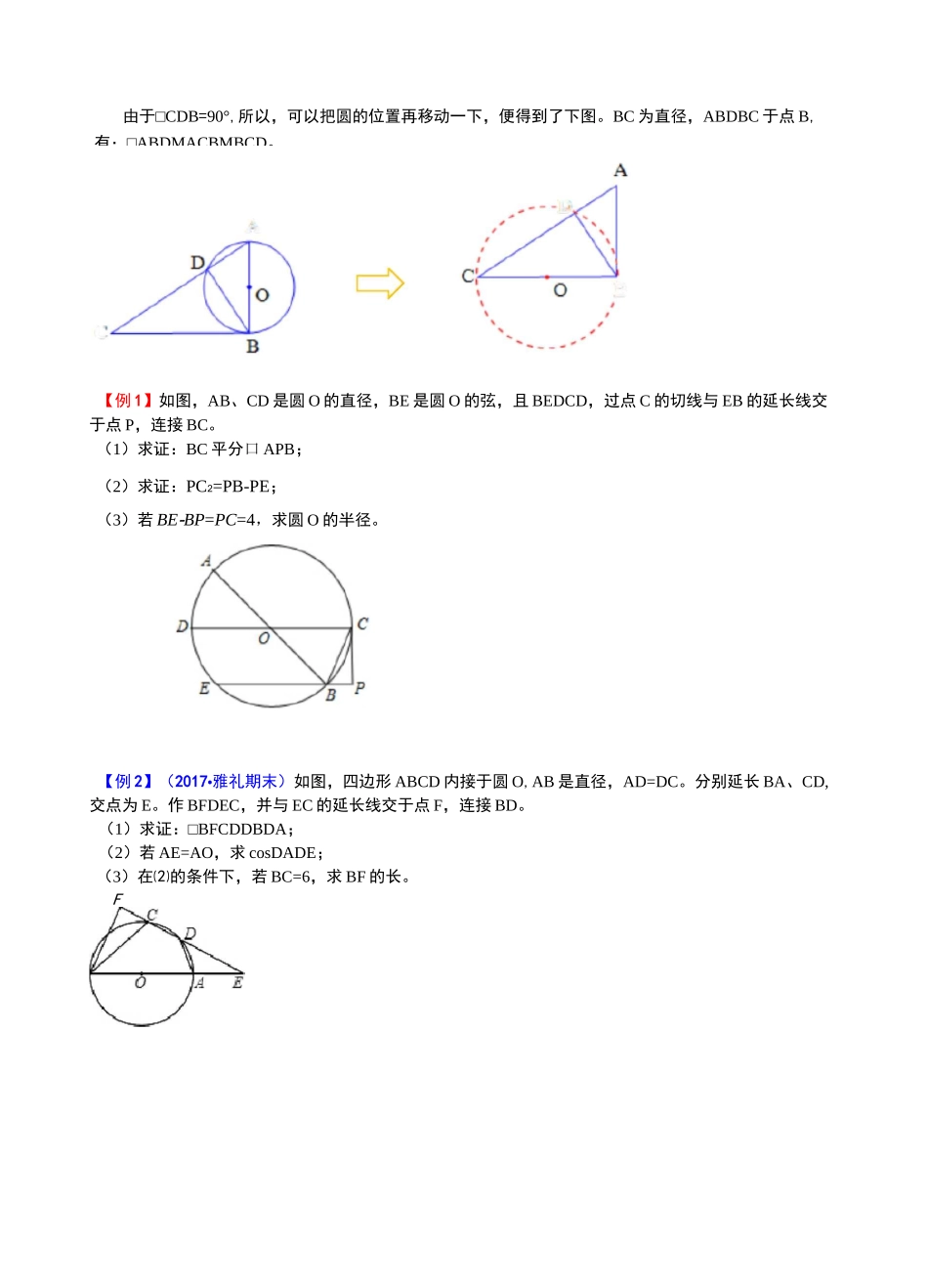
圆的综合类型1:圆割(切)线产生的相似图形(1)如图,AD和AE与圆O相交,则有:□ABCDDADE。如果把图形剥离出来,就是我们常见的A型相似。证明:【变化】若弦DEDBC,便得平行线A型相似。(2)现在,我们把AE绕点A顺时针旋转,旋转至AE与圆O相切的位置,记切点为B,此时,相当于点B与点E重合于点B,有:□ABCDDABD,此图为切割线定理的基本图形,如下图;若把圆去掉,变得到了“母子型”相似。证法一】如下图:证法二】如下图:ACCAAOccBAEEBCF类型二:相交弦产生的相似图形(3)如图,弦AB、CD相较于点E,则有:□AECMDEB,△AED^^CEB。若把圆去掉,变得到8字相似模型,如下图:证明:【变化】若是把弦AC、BD调整为平行的两条弦,便得到平行线8字模型。这个基本图形,还在如下两类图形里经常出现,如下图:类型三:直径所对的圆周而产生的相似模型(4)如图,BC与圆O相切于点B,AC与圆O相交于点D,AB为圆O的直径,有:□ABDMACBMBCD。若把圆O去掉,便得到了基本的垂直相似模型,如下图:由于口ABC=90°,所以,可以把圆的位置移动一下,便得到了下图。AC为直径,BDDAC于点D,有:□ABDMACBMBCD。有:□ABDMACBMBCD。DABc由于□CDB=90°,所以,可以把圆的位置再移动一下,便得到了下图。BC为直径,ABDBC于点B,【例1】如图,AB、CD是圆O的直径,BE是圆O的弦,且BEDCD,过点C的切线与EB的延长线交于点P,连接BC。(1)求证:BC平分口APB;(2)求证:PC2=PB-PE;(3)若BE-BP=PC=4,求圆O的半径。【例2】(2017•雅礼期末)如图,四边形ABCD内接于圆O,AB是直径,AD=DC。分别延长BA、CD,交点为E。作BFDEC,并与EC的延长线交于点F,连接BD。(1)求证:□BFCDDBDA;(2)若AE=AO,求cosDADE;(3)在⑵的条件下,若BC=6,求BF的长。F【例3】(2017・南雅期末)如图,已知DABC中,BA=BC,以AB为直径的圆O与AC交于D点,过点D作DFDBC交AB的延长线于点E,垂足为F。(1)证明:DE为圆O的切线;1(2017•青竹湖期末)如图,点A、B、C是圆O上的三点,ABDOC。(1)求证:AC平分DOAB;(2)过点O作OEDAB于点E,交AC于点P,若AB=4,OP=2PE,求圆O的半径长和OP的长。2、(2017・师大附中期末)如图,DABC内接于圆O,AD是圆O直径,E是CB延长线上一点,且□BAE=DC。(1)求证:直线AE是圆O的切线;(2)若口BAE=30°,圆O的半径为2,求阴影部分的面积;4(3)若EB=AB,cosE=5,AE=24,求EB的长及圆O的半径。求证:CE=CB;连接AF、BF,求口ABF的正弦值;4(2017•长郡期末)如图,AB是圆O的弦,D为半径OA的中点,过D作CDDOA交弦AB于点E,交圆O于点F,且BC是圆O的切线。(1(2)5(2018雅礼第三次月考)如图,AB是圆O的直径,点D、E在圆O上,mA=2DBDE,点C在AB的延长线上,□C=DABD。(1)求证:CE是圆O的切线;(2)连接BE,求证:□CEB=DBDE。(3)若BF=2,EF二<11,求圆O的半径。3(2017・明德期末)如图,在DABC中,口。=90。,点O在AC上,以OA为半径的圆O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE。(1)判断直线DE与圆O的位置关系,并说明理由;(2)若AC=6,BC=8,OA=2,求线段DE的长。6、如图,已知圆O为DABC的外接圆,且AB=AC,过A作AF交CB的延长线于点F,交圆O于点E,连接BE,D为弧AC上一点,连接AD、CD,且BE=AD。(1)求证:□ADCDDFBA;(2)若AB=6,DC=3,求tanDCAD的值。7、如图,CD是0O的切线,点C在直径AB的延长线上.(1)求证:ZCAD=ZBDC;2(2)若BD=3AD,AC=3,求CD的长.8、(2017・广益第三次月考)如图,△ABC内接于圆O,CD平分ZACB交圆O于D,过点D作PQ〃AB分别交CA、CB延长线于P、Q。连接BD。(1)求证:PQ是圆O的切线;(2)求证:BD2二AC-BQ;41(3)若AC、BQ的长是关于x的方程x+—=m的两实根,且tanZPCD=三,求圆O的半径。x3