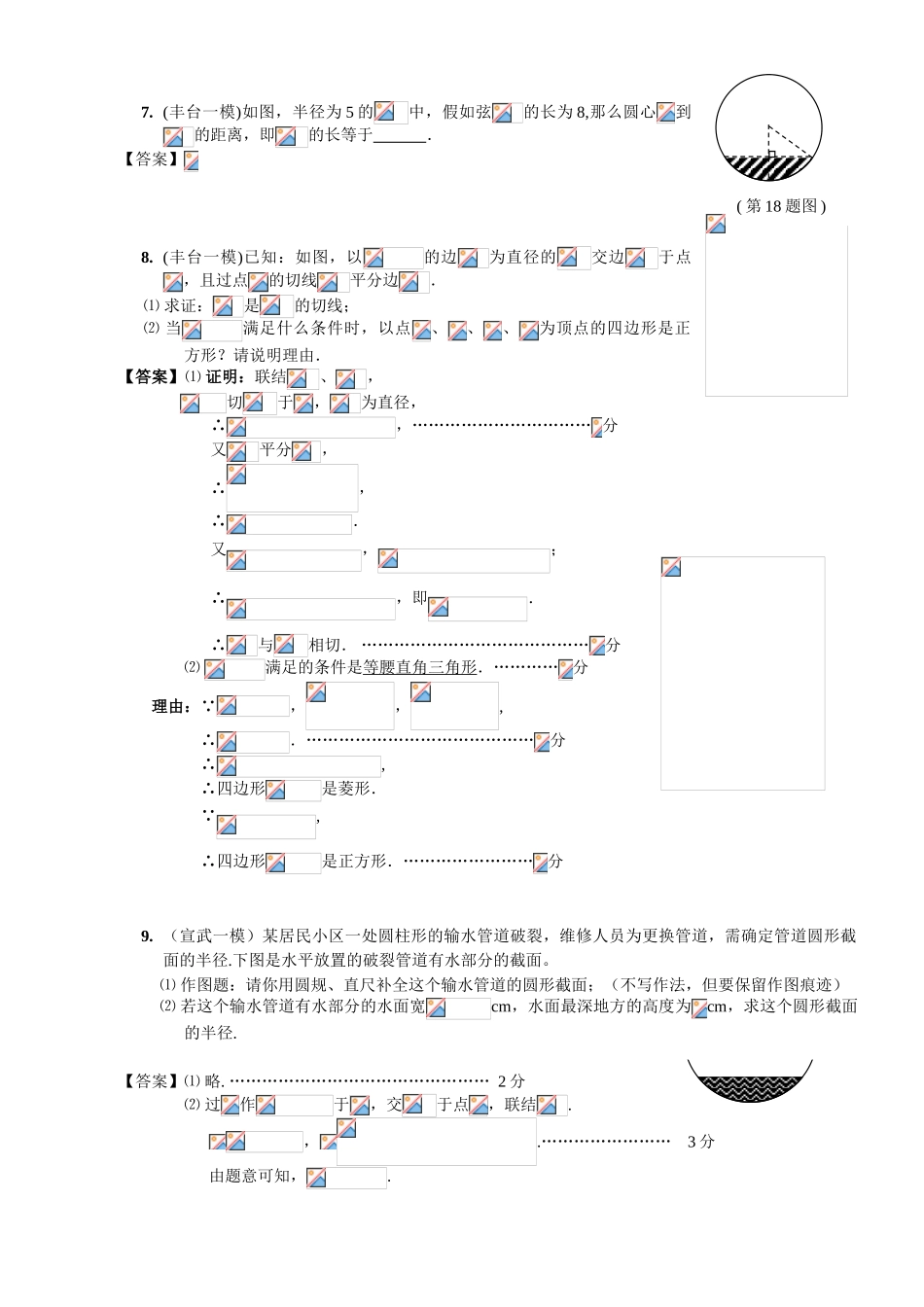
2024-2024年中考模拟分类汇编(VI)圆1.(海淀一模)已知:如图,圆心角,则圆周角的度数为()【答案】选D.2.(昌平二模)已知:如图,A、B、C是⊙O上的三个点,∠AOC=100°,则∠ABC的度数为()A.30°B.45°C.50°D.60°【答案】C3.(朝阳一模)如图,中,,,以为圆心,为半径的圆交于点,若,则的长为________.【答案】4.(朝阳一模)已知等腰三角形内接于半径为的中,假如底边的长为,那么底角的正切值是________.【答案】或5.(宣武一模)⊙的半径cm,圆心到直线的距离cm,在直线上有一点且cm,则点().(A)在⊙内(B)在⊙上(C)在⊙外(D)可能在⊙内也可能在⊙外【答案】6.(丰台一模)如图,假如将半径为9cm的圆形纸片剪去一个圆周的扇形,用剩下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面圆半径为()A.B.C.D.【答案】A剪去7.(丰台一模)如图,半径为5的中,假如弦的长为8,那么圆心到的距离,即的长等于.【答案】8.(丰台一模)已知:如图,以的边为直径的交边于点,且过点的切线平分边.⑴求证:是的切线;⑵当满足什么条件时,以点、、、为顶点的四边形是正方形?请说明理由.【答案】⑴证明:联结、,切于,为直径,∴,……………………………分又平分,∴,∴.又,;∴,即.∴与相切.……………………………………分⑵满足的条件是等腰直角三角形.…………分理由: ,,,∴.……………………………………分∴,∴四边形是菱形. ,∴四边形是正方形.……………………分9.(宣武一模)某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径.下图是水平放置的破裂管道有水部分的截面。⑴作图题:请你用圆规、直尺补全这个输水管道的圆形截面;(不写作法,但要保留作图痕迹)⑵若这个输水管道有水部分的水面宽cm,水面最深地方的高度为cm,求这个圆形截面的半径.【答案】⑴略.…………………………………………2分⑵过作于,交于点,联结.,.……………………3分由题意可知,.(第18题图)设半径为,则.在中,由勾股定理得:,.……………5分.即这个圆形截面的半径为.……………6分10.(石景山二模)如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3cm,则此光盘的直径是_____cm.【答案】11.(石景山二模)如图是不倒翁的正视图,不倒翁的圆形脸恰好与帽子边沿PA、PB分别相切于点A、B,不倒翁的鼻尖正好是圆心O.⑴若∠OAB=25°,求∠APB的度数;⑵若∠OAB=n°,请直接写出∠APB的度数.【答案】⑴ PA、PB切⊙O于A、B,∴PA=PB.………………………………………………1分∴OA⊥PA.……………………………………………2分 ∠OAB=25°,∴∠PAB=65°.………………………3分∴∠APB=180°-65°×2=50°.………………………4分⑵2n.…………………………5分12.(石景山二模)如图,Rt△ABC中,∠C=90°,∠B的平分线交AC于E,DE⊥BE.⑴试说明AC是△BED外接圆的切线;⑵若CE=1,BC=2,求△ABC内切圆的面积.【答案】⑴取BD的中点O,联结OE. OE=OB,∴∠OBE=∠OEB.又∠0BE=∠CBE,∴∠CBE=∠OEB.∴BC∥OE.………………1分∴∠OEA=∠C=90°.∴AC⊥OE.∴AC是△BED外接圆的切线.…………………2分⑵Rt△BCE中,BE==. ∠OBE=∠OEB,∠C=∠BED=90°,∴△BCE∽△BED.∴.………………………3分∴DE=,∴BD=.∴OE=OB=OD= BC∥OE,∴.∴AE=,AO=.…………………………………………………4分∴△ABC的内切圆半径为r=(BC+AC-AB)=.………………………5分∴△ABC的内切圆面积为.………………………………………………6分13.(海淀一模)已知:如图,是的直径,是弦,是过点的直线,等于半径长.⑴若,求证:是的切线;⑵在⑴成立的条件下,当点是的中点时,在上截取,连接、、,求证:是等边三角形.【答案】⑴连接, 是的直径,是弦,且等于半径长∴,∴为等边三角形,∴,∴,∴∴,且为直径,∴是的切线⑵连接,,由是的中点,可得,易证:,∴,,可证得∴是等边三角形.14.(海淀一模)在一个夹角为的墙角放置了一个圆形的容器,俯视图如图,在俯视图中圆与两边的...