高三数学滚动练习十三 VIP免费

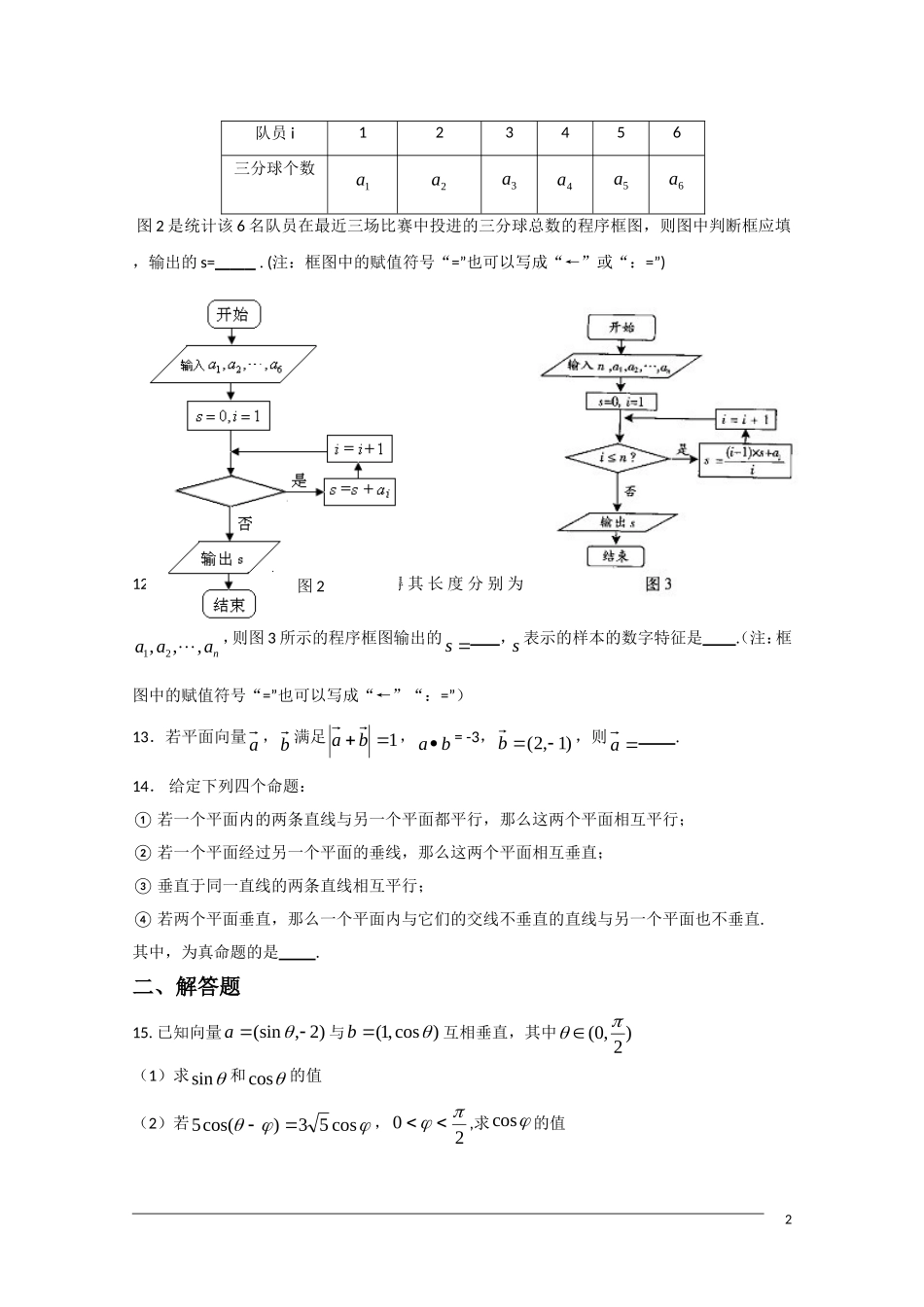
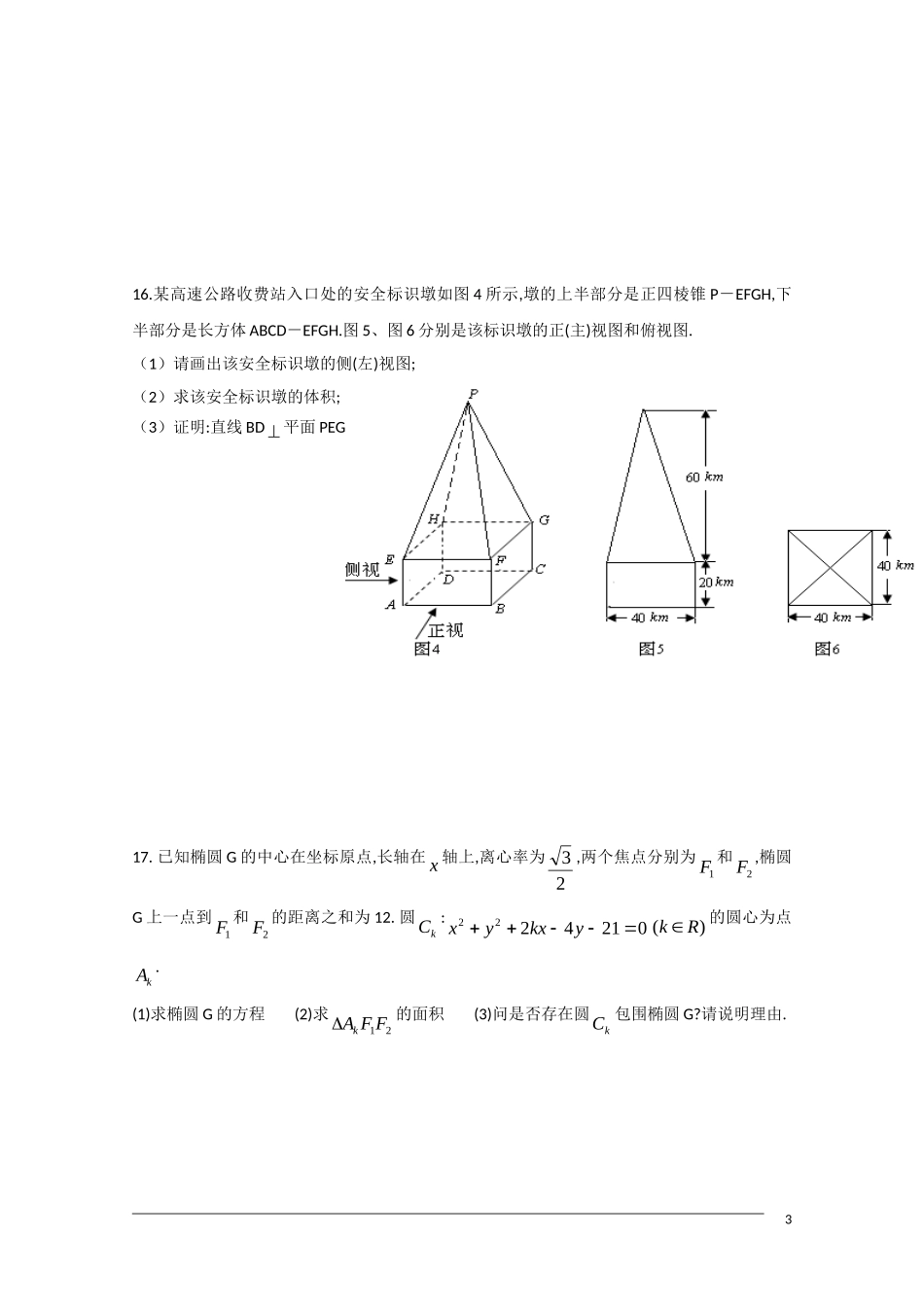
高三数学滚动练习十三一、填空题1.已知全集U=R，则正确表示集合M={－1，0，1}和N={x|x2+x=0}关系的韦恩（Venn）图是.2.函数1)4(cos22xy的周期是.3.设z是复数，()az表示满足1nz的最小正整数n，则对虚数单位i，()ai.4.以点（2，1）为圆心且与直线6xy相切的圆的方程是.5.已知等比数列}{na的公比为正数，且3a·9a=225a，2a=1，则1a=.6.某单位200名职工的年龄分布情况如图1，现要从中抽取40名职工作样本，用系统抽样法，将全体职工随机按1－200编号，并按编号顺序平均分为40组（1－5号，6－10号…，196－200号）.若第5组抽出的号码为22，则第8组抽出的号码应是；若用分层抽样方法，则40岁以下年龄段应抽取人.7.一质点受到平面上的三个力123,,FFF（单位：牛顿）的作用而处于平衡状态．已知1F，2F成060角，且1F，2F的大小分别为2和4，则3F的大小为.8.函数xexxf)3()(的单调递增区间是.9.已知ABC中，CBA,,的对边分别为a,b,c若a=c=26且75Ao，则b=.10.已知等比数列{}na满足0,1,2,nan，且25252(3)nnaan，则当1n时，2123221logloglognaaak.11.某篮球队6名主力队员在最近三场比赛中投进的三分球个数如下表所示：1图1队员i123456三分球个数1a2a3a4a5a6a图2是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图，则图中判断框应填，输出的s=.(注：框图中的赋值符号“=”也可以写成“←”或“：=”)12．随机抽取某产品n件，测得其长度分别为12,,,naaa，则图3所示的程序框图输出的s，s表示的样本的数字特征是.（注：框图中的赋值符号“=”也可以写成“←”“：=”）13．若平面向量a，b满足1ba，ab=-3，)1,2(b，则a.14．给定下列四个命题：①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；③垂直于同一直线的两条直线相互平行；④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.其中，为真命题的是.二、解答题15.已知向量)2,(sina与)cos,1(b互相垂直，其中)2,0(（1）求sin和cos的值（2）若cos53)cos(5，02,求cos的值2图216.某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P－EFGH,下半部分是长方体ABCD－EFGH.图5、图6分别是该标识墩的正(主)视图和俯视图.（1）请画出该安全标识墩的侧(左)视图;（2）求该安全标识墩的体积;（3）证明:直线BD平面PEG.17.已知椭圆G的中心在坐标原点,长轴在x轴上,离心率为23,两个焦点分别为1F和2F,椭圆G上一点到1F和2F的距离之和为12.圆kC:0214222ykxyx)(Rk的圆心为点kA.(1)求椭圆G的方程(2)求21FFAk的面积(3)问是否存在圆kC包围椭圆G?请说明理由.318.已知点（1，31）是函数,0()(aaxfx且1a）的图象上一点，等比数列}{na的前n项和为cnf)(,数列}{nb)0(nb的首项为c，且前n项和nS满足nS－1nS=nS+1nS（n2）.(1)求数列}{na和}{nb的通项公式;(2)若数列{}11nnbb前n项和为nT，问nT>20091000的最小正整数n是多少?19.已知二次函数)(xgy的导函数的图像与直线2yx平行,且)(xgy在x=－1处取得最小值m－1(m0).设函数xxgxf)()((1)若曲线)(xfy上的点P到点Q(0,2)的距离的最小值为2,求m的值；(2))(Rkk如何取值时,函数kxxfy)(存在零点,并求出零点.4