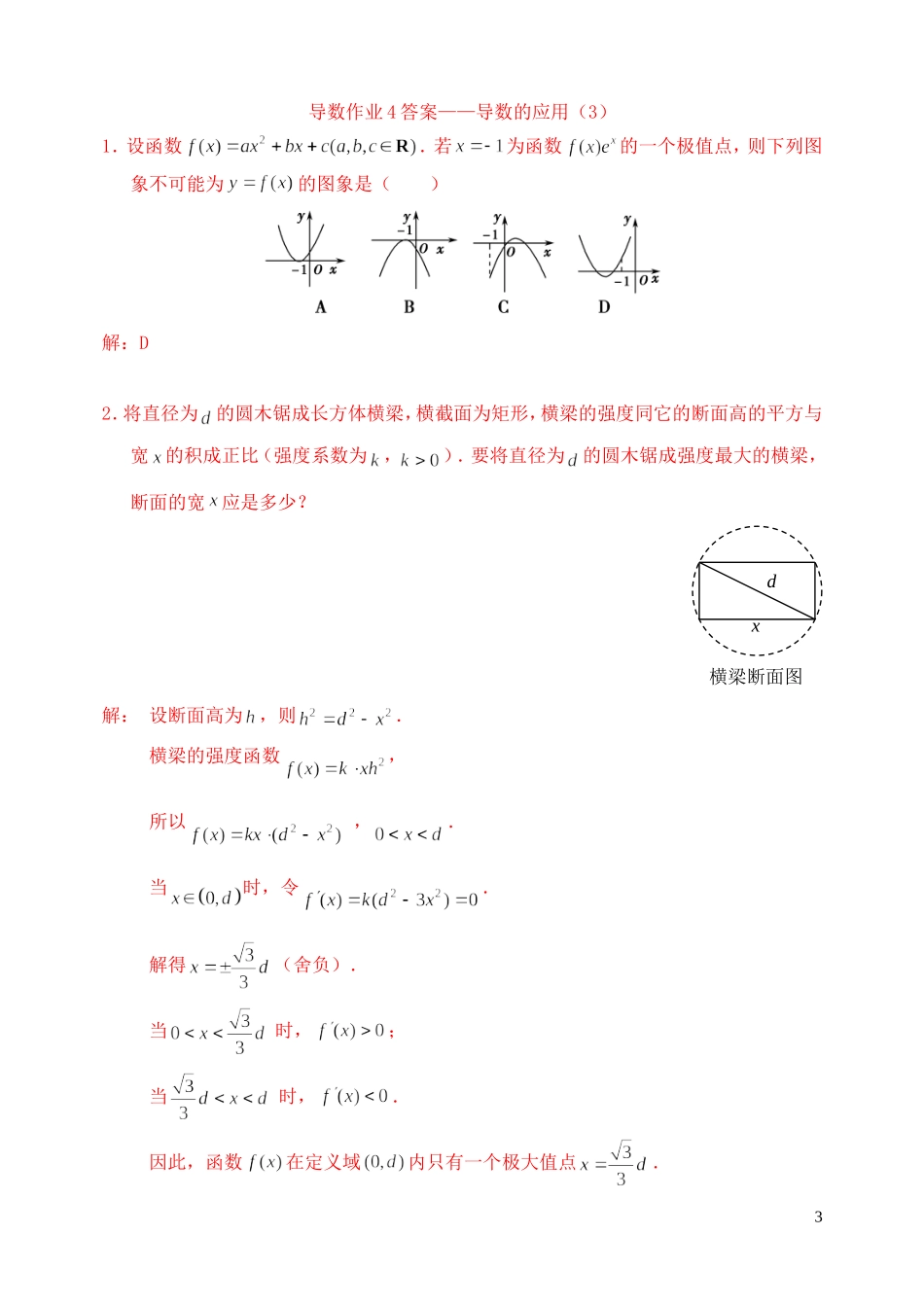
北京八中2016届高三数学（理科）复习导数作业4导数的应用（3）1．设函数．若为函数的一个极值点，则下列图象不可能为的图象是（）2．将直径为的圆木锯成长方体横梁，横截面为矩形，横梁的强度同它的断面高的平方与宽的积成正比（强度系数为，）．要将直径为的圆木锯成强度最大的横梁，断面的宽应是多少
3．已知函数（其中）．（Ⅰ）若函数在点处的切线为，求实数的值；（Ⅱ）求函数的单调区间．横梁断面图dx14．已知函数．（Ⅰ）当时，求函数的单调区间；（Ⅱ）若函数在上的最小值是，求的值．2导数作业4答案——导数的应用（3）1．设函数．若为函数的一个极值点，则下列图象不可能为的图象是（）解：D2．将直径为的圆木锯成长方体横梁，横截面为矩形，横梁的强度同它的断面高的平方与宽的积成正比（强度系数为，）．要将直径为的圆木锯成强度最大的横梁，断面的宽应是多少
解：设断面高为，则．横梁的强度函数，所以，．当时，令．解得（舍负）．当时，；当时，．因此，函数在定义域内只有一个极大值点．横梁断面图dx3所以在处取最大值，就是横梁强度的最大值．即当断面的宽为时，横梁的强度最大．3．已知函数（其中）．（Ⅰ）若函数在点处的切线为，求实数的值；（Ⅱ）求函数的单调区间．解：由，可得
（Ⅰ）因为函数在点处的切线为，得:解得（Ⅱ）令，得…①当，即时，不等式①在定义域内恒成立，所以此时函数的单调递增区间为和
当，即时，不等式①的解为或，又因为，所以此时函数的单调递增区间为和，单调递减区间为和
所以，当时，函数的单调递增区间为和；当时，函数的单调递增区间为和，单调递减区间为和
44．已知函数．（Ⅰ）当时，求函数的单调区间；（Ⅱ）若函数在上的最小值是，求的值．解：函数的定义域为（0，+∞），（Ⅰ）∵，∴，故函数在其定义域（0，+∞）上是单调递增的．（Ⅱ）在[1,e]上，分如下情况讨论：①当a
