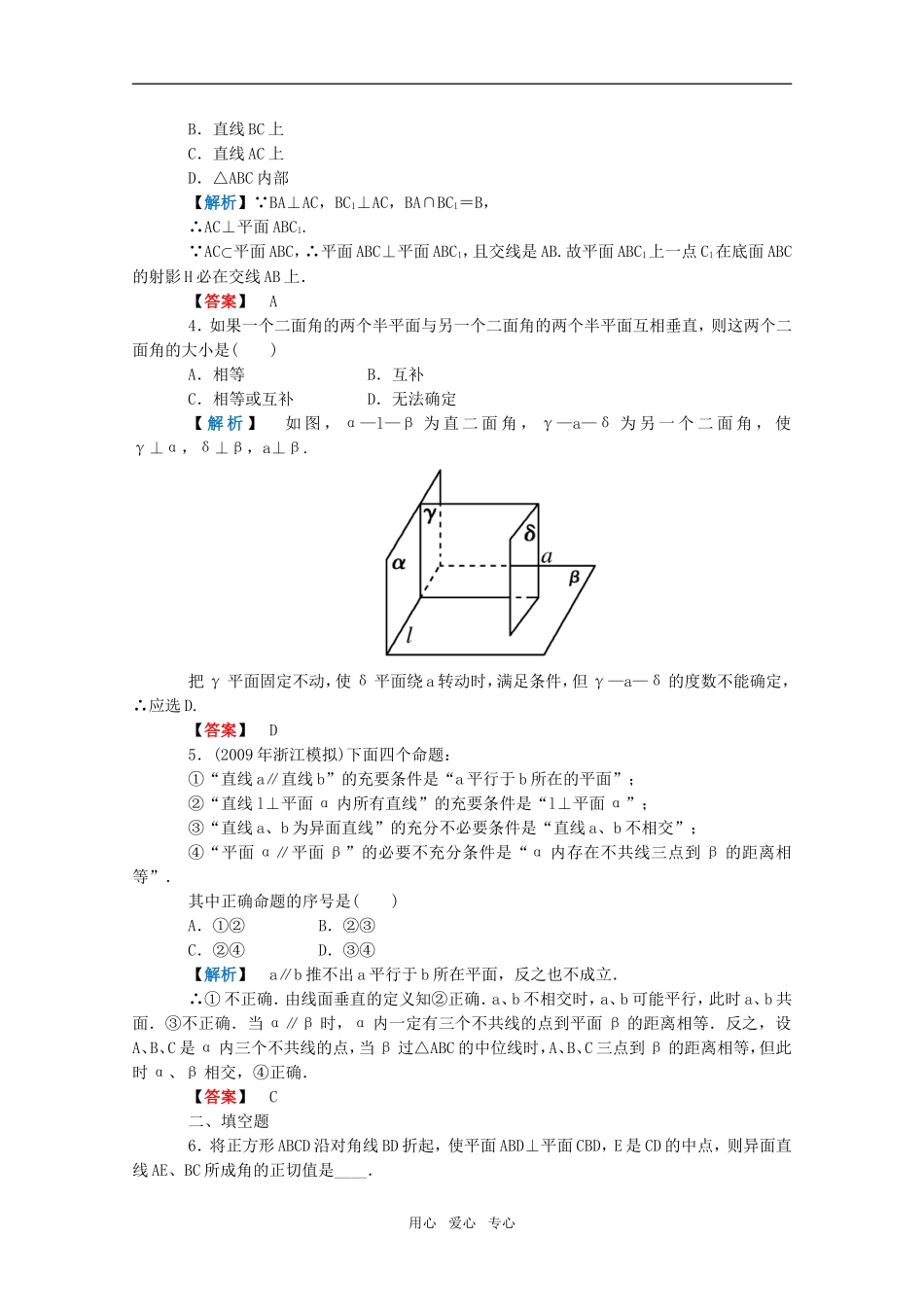
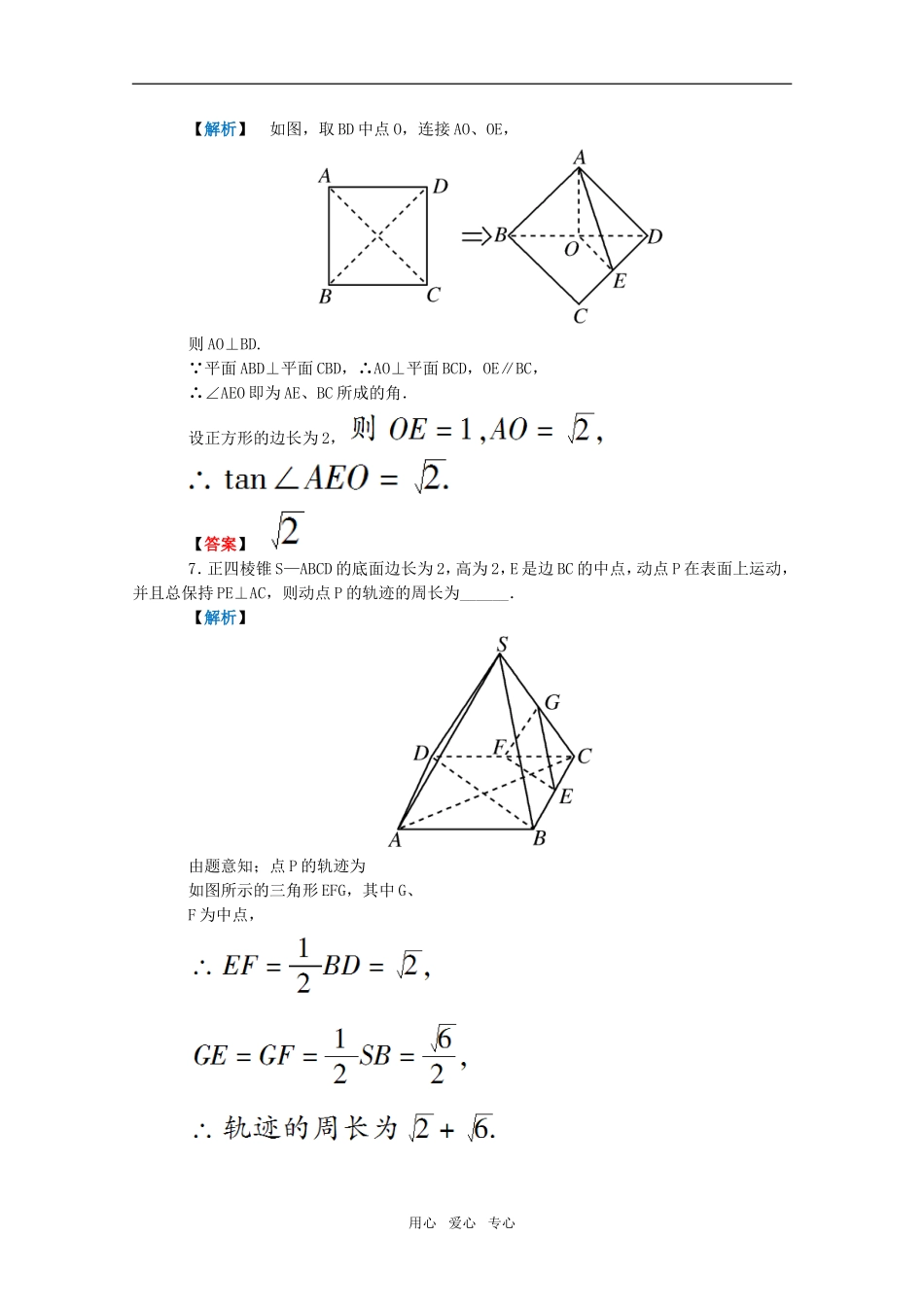
(本栏目内容,学生用书中以活页形式单独装订成册!)一、选择题1.若m、n是两条不同的直线,α、β、γ是三个不同的平面,则下列命题中的真命题是()A.若m⊂β,α⊥β,则m⊥αB.若α∩γ=m,β∩γ=n,m∥n,则α∥βC.若m⊥β,m∥α,则α∥βD.若α⊥γ,α⊥β,则β⊥γ【解析】A中只有当m垂直于α、β的交线时,才有m⊥α;B中α、β可能相交,如三棱柱的两个侧面;C中m∥α⇒α内有一直线D中,β与γ可能平行,也可能相交(不一定垂直).【答案】C2.(2009年柳州模拟)设a、b是不同的直线,α、β是不同的平面,则下列四个命题中正确的是()A.若a⊥b,a⊥α,则b∥αB.若a∥α,α⊥β,则a⊥βC.若a⊥β,α⊥β,则a∥αD.若a⊥b,a⊥α,b⊥β,则α⊥β【解析】A中,b可能在α内;B中,a可能在β内,也可能与β平行或相交(不垂直);C中,a可能在α内;D中,a⊥b,a⊥α,则b⊂α或b∥α,又b⊥β,∴α⊥β.【答案】D3.如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在底面ABC上的射影H必在()A.直线AB上用心爱心专心B.直线BC上C.直线AC上D.△ABC内部【解析】 BA⊥AC,BC1⊥AC,BA∩BC1=B,∴AC⊥平面ABC1. AC⊂平面ABC,∴平面ABC⊥平面ABC1,且交线是AB.故平面ABC1上一点C1在底面ABC的射影H必在交线AB上.【答案】A4.如果一个二面角的两个半平面与另一个二面角的两个半平面互相垂直,则这两个二面角的大小是()A.相等B.互补C.相等或互补D.无法确定【解析】如图,α—l—β为直二面角,γ—a—δ为另一个二面角,使γ⊥α,δ⊥β,a⊥β.把γ平面固定不动,使δ平面绕a转动时,满足条件,但γ—a—δ的度数不能确定,∴应选D.【答案】D5.(2009年浙江模拟)下面四个命题:①“直线a∥直线b”的充要条件是“a平行于b所在的平面”;②“直线l⊥平面α内所有直线”的充要条件是“l⊥平面α”;③“直线a、b为异面直线”的充分不必要条件是“直线a、b不相交”;④“平面α∥平面β”的必要不充分条件是“α内存在不共线三点到β的距离相等”.其中正确命题的序号是()A.①②B.②③C.②④D.③④【解析】a∥b推不出a平行于b所在平面,反之也不成立.∴①不正确.由线面垂直的定义知②正确.a、b不相交时,a、b可能平行,此时a、b共面.③不正确.当α∥β时,α内一定有三个不共线的点到平面β的距离相等.反之,设A、B、C是α内三个不共线的点,当β过△ABC的中位线时,A、B、C三点到β的距离相等,但此时α、β相交,④正确.【答案】C二、填空题6.将正方形ABCD沿对角线BD折起,使平面ABD⊥平面CBD,E是CD的中点,则异面直线AE、BC所成角的正切值是____.用心爱心专心【解析】如图,取BD中点O,连接AO、OE,则AO⊥BD. 平面ABD⊥平面CBD,∴AO⊥平面BCD,OE∥BC,∴∠AEO即为AE、BC所成的角.设正方形的边长为2,【答案】7.正四棱锥S—ABCD的底面边长为2,高为2,E是边BC的中点,动点P在表面上运动,并且总保持PE⊥AC,则动点P的轨迹的周长为______.【解析】由题意知;点P的轨迹为如图所示的三角形EFG,其中G、F为中点,用心爱心专心【答案】8.设P是60°的二面角α—l—β内一点,PA⊥α,PB⊥β,A、B分别为垂足,PA=2,PB=4,则AB的长是________.【解析】设平面PAB与棱l交于点O,连接AO、BO,则∠AOB为二面角的平面角,∴∠AOB=60°,∴∠APB=120°.∴AB2=AP2+BP2-2AP·BP·cos120°【答案】三、解答题9.(2009年年苏北模拟)在四棱锥S—ABCD中,已知AB∥CD,SA=SB,SC=SD,E、F分别为AB、CD的中点.(1)求证:平面SEF⊥平面ABCD;(2)若平面SAB∩平面SCD=l,求证:AB∥l.【证明】(1)由SA=SB,E为AB中点得SE⊥AB.由SC=SD,F为CD中点得SF⊥DC.又AB∥DC,∴SB⊥SF.又SF∩SE=S,∴AB⊥平面SEF.又 AB⊂平面ABCD,∴平面SEF⊥平面ABCD.(2) AB∥CD,CD⊂平面SCD,∴AB∥平面SCD.又 平面SAB∩平面SCD=l,用心爱心专心根据直线与平面平行的性质定理得:AB∥l.10.(2009年九江模拟)如图,四棱锥S—ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上一动点.(1)求证:平面EBD⊥平面SAC;(2)当的值为多少时,二面角B—SC—D的大小为120...