高三数学 圆锥曲线讲解及练习稿VIP免费

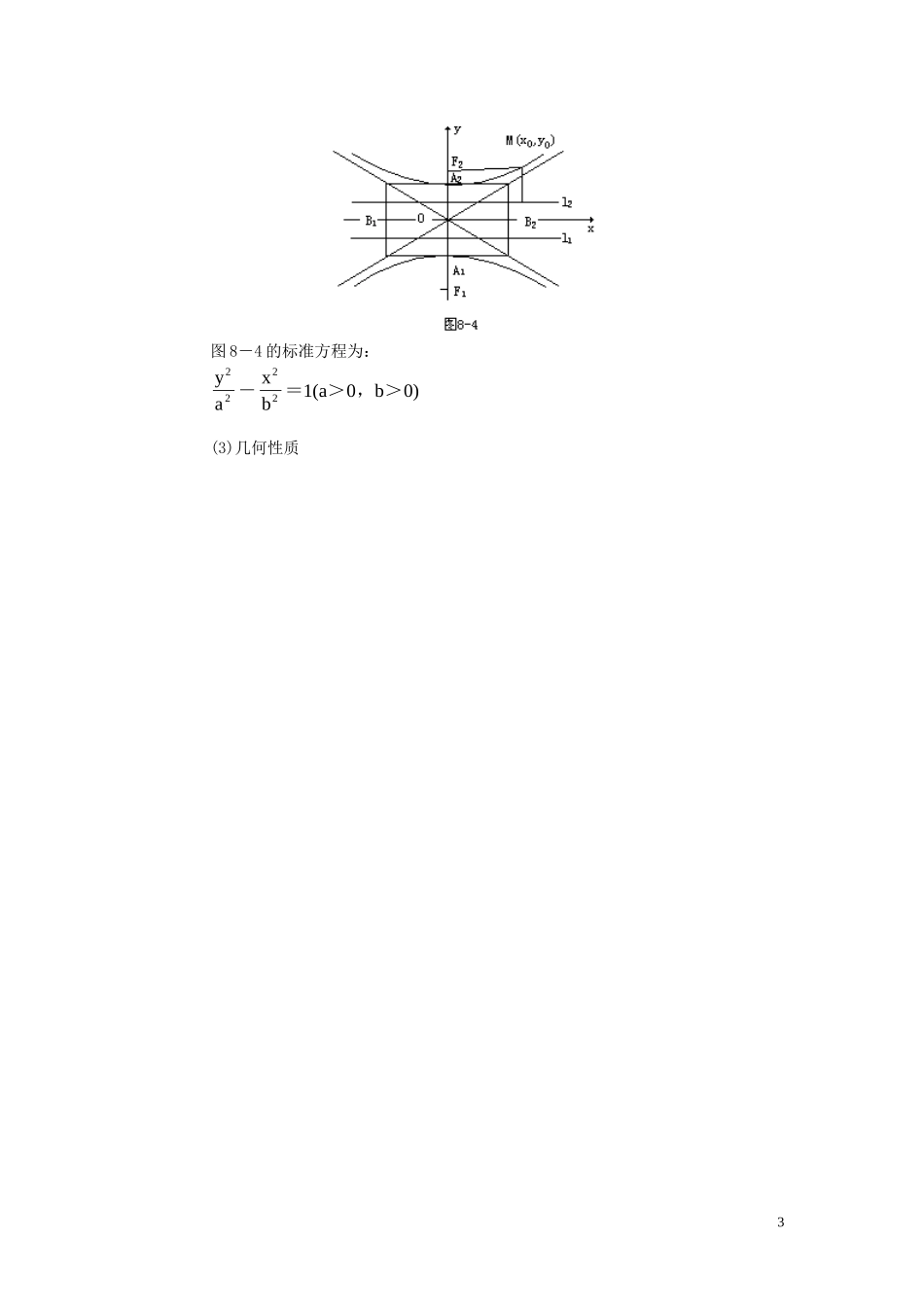
圆锥曲线一、基本知识1．椭圆(1)定义定义1：平面内一个动点到两个定点F1、F2的距离之和等于常数(大于|F1F2|)，这个动点的轨迹叫椭圆(这两个定点叫焦点)．定义2：点M与一个定点的距离和它到一条定直线的距离的比是常数＝＜＜时，这个点的轨迹是椭圆．e(0e1)ca(2)图形和标准方程图－的标准方程为：＋＝＞＞图－的标准方程为：＋＝＞＞811(ab0)821(ab0)xaybxbya22222222(3)几何性质条件{M|MF1|+|MF2|=2a，2a＞|F1F2|}{M||MF|Ml=|MF|Ml=e0e1}1122点到的距离点到的距离，＜＜标准方程xaybab222210()＞＞xbyaab222210()＞＞顶点A1(－a，0)，A2(a，0)B1(0，－b)，B2(0，b)A1(0，－a)，A2(0，a)B1(－b，0)，B2(b，0)轴对称轴：x轴，y轴．长轴长|A1A2|=2a，短轴长|B1B2|=2b焦点F1(－c，0)，F2(c，0)F1(0，－c)，F2(0，c)焦距|F1F2|=2c(c＞0)，c2=a2－b21离心率e(0e1)＝＜＜ca准线方程ll12xx：＝；：＝acac22ll12yy：＝；：＝acac22焦点半径|MF1|＝a＋ex0，|MF2|＝a－ex0|MF1|＝a＋ey0，|MF2|＝a－ey0点和椭圆的关系＞外在椭圆上＜内xaybxy022022001(,)(k为切线斜率)，ykx＝±akb222(k为切线斜率)，ykx＝±bka222切线方程xxayyb0202＋＝1(x0，y0)为切点xxbyya0202＋＝1(x0，y0)为切点切点弦方程(x0，y0)在椭圆外xxayyb0202＋＝1(x0，y0)在椭圆外xxbyya0202＋＝1弦长公式|xx|1+k|yy|1+1k212122－或－其中(x1，y1)，(x2，y2)为割弦端点坐标，k为割弦所在直线的斜率2．双曲线(1)定义定义1：平面内与两个定点F1、F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线(这两个定点叫双曲线的焦点)．定义2：动点到一定点的距离与它到一条定直线的距离之比是常数e(e＞1)时，这个动点的轨迹是双曲线(这定点叫做双曲线的焦点)．(2)图形和标准方程图8－3的标准方程为：xayb2222－＝＞，＞1(a0b0)2图8－4的标准方程为：yaxb2222－＝＞，＞1(a0b0)(3)几何性质3条件P＝{M|MF1|－|MF2|＝2a，a＞0，2a＜|F1F2|}．P{M||MF|Ml|MF|Mlee1}1122＝点到的距离＝点到的距离＝，＞．标准方程xayb2222－＝＞，＞1(a0b0)yaxb2222－＝＞，＞1(a0b0)顶点A1(－a，0)，A2(a，0)A1(0，－a)，A2(0，a)轴对称轴：x轴，y轴，实轴长|A1A2|＝2a，虚轴长|B1B2|＝2b焦点F1(－c，0)，F2(c，0)F1(0，－c)，F2(0，c)焦距|F1F2|＝2c(c＞0)，c2＝a2＋b2离心率e(e1)＝＞ca准线方程ll12xx：＝－；：＝acac22ll12yy：＝－；：＝acac22渐近线方程yx(0)＝±或－＝baxayb2222yx(0)＝±或－＝abyaxb2222共渐近线的双曲线系方程xayb2222－＝≠k(k0)yaxb2222－＝≠k(k0)焦点半径|MF1|＝ex0＋a，|MF2|＝ex0－a|MF1|＝ey0＋a，|MF2|＝ey0－aykx＝±akb222(k为切线斜率)kk＞或＜－babaykx＝±bka222(k为切线斜率)kk＞或＜－ababxxayyb0202－＝1((x0，y0)为切点yyaxxb0202－＝1((x0，y0)为切点切线方程xyaa((xy)2200＝的切线方程：＝，为切点xyyx002切点弦方程(x0，y0)在双曲线外xxayyb0202－＝1(x0，y0)在双曲线外yyaxxb0202－＝1弦长公式|xx|1+k|yy|1+1k212122－或－其中(x1，y1)，(x2，y2)为割弦端点坐标，k为割弦所在直线的斜率3．抛物线(1)定义平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线，定点F叫做抛物线的焦点，定直线l叫做抛物线的准线．4(2)抛物线的标准方程，类型及几何性质，见下表：①抛物线的标准方程有以下特点：都以原点为顶点，以一条坐标轴为对称轴；方程不同，开口方向不同；焦点在对称轴上，顶点到焦点的距离等于顶点到准线距离．②p的几何意义：焦点F到准线l的距离．③弦长公式：设直线为＝＋抛物线为＝，＝ykxby2px|AB|212k|xx||yy|2121－＝－112k焦点弦长公式：|AB|＝p＋x1＋x2④关于抛物线焦点弦的几个结论：设AB为过抛物线焦点的弦，A（，直线AB的倾斜角为，则ⅰ）；ⅱ）ⅲ）以AB为直径的圆与准线相切ⅳ）⑤设F是抛物线的焦点，M是抛物线上任一点，则⑥过抛物线的焦点F作垂直于对称轴的直线，交抛物线于A、B两点，则线段AB称为抛物线的通径，其长为4．圆锥曲线(椭圆、双曲线、抛物线统称圆锥曲线)的统一定义与一定点的距离和一条定直线的距离的比等于常数的点的...