高三数学 反函数、二次函数、幂、指、对数式 知识精讲VIP免费

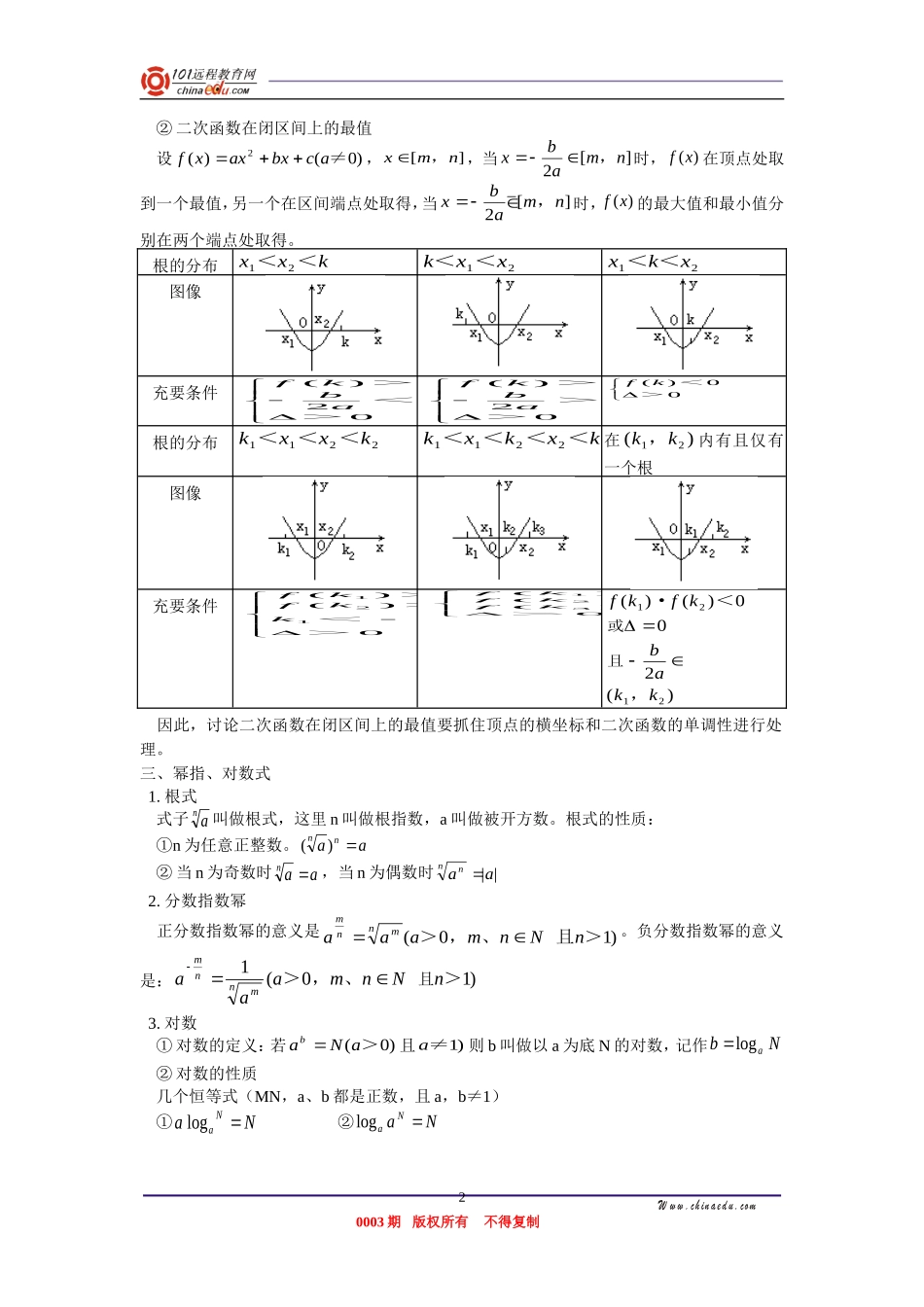
高三数学反函数、二次函数、幂、指、对数式知识精讲一、反函数1.函数yfx()存在反函数的条件若函数yfx()有定义域为A，值域为B，对于B中每一个元素y0，在A中都有唯一确定的元素x0与之对应，则函数yfx()存在反函数，记为yfx1()，否则，就不存在反函数。2.互为反函数的图像之间的关系互为反函数的图像关于直线yx对称由此可得到如下结论：①反函数的定义域是原函数的值域，反函数的值域是原函数的定义域②fabfba1()()③函数yfx()与xfy1()的图像完全相同。④互为反函数的两个函数具有相同的单调性和奇偶性。3.求yfx()的反函数的一般步骤①确定原函数的值域，也就是反函数的定义域②由yfx()的解析式解出xfy1()③将x、y对换、得反函数的习惯表达式yfx1()并注明定义域二、二次函数1.二次函数的基本知识（1）定义：形如fxaxbxca()()20≠的函数叫做二次函数。（2）图像：二次函数yaxbxca20()≠的图像是以直线xba2为对称轴的抛物线，其开口方向由a的符号确定，顶点坐标为()baacba2442，。（3）性质：二次函数yaxbxca20()≠的单调性是以项点的横坐标xba2分界。当a＞0时，xba(]，，2fx()单调递减，xba[)2，，fx()单调递增。当a＜0时，xbafx(]()，，2单调递增，xbafx[]()2，，单调递减。2.二次函数的解析式（1）一般式fxaxbxca()()20≠；（2）顶点式fxaxkha()()()20≠；（3）零点式fxaxxxxa()()()()120·≠；求解析式都是用待定系数法。3.二次函数的应用二次函数虽是初中所学内容，但它在高中学习中起到非常重要的作用，贯穿高中全部学习过程，同时也是高考要考的主要内容之一，二次函数的应用很广，利用二次函数图像可以求解一元二次方程和讨论一元二次方程的实根分布情况，还可以讨论二次函数在闭区间上的最值，这些既是学习的重点又是学习中的难点。①根的分布：设fxaxbxca()()20＞，如下图所示。Www.chinaedu.com0003期版权所有不得复制1②二次函数在闭区间上的最值设fxaxbxca()()20≠，xmn[]，，当xbamn2[]，时，fx()在顶点处取到一个最值，另一个在区间端点处取得，当xbamn2[]，时，fx()的最大值和最小值分别在两个端点处取得。根的分布xxk12＜＜kxx＜＜12xkx12＜＜图像充要条件fkbak()＞＜＞020fkbak()＞＞＞020fk()＜＞00根的分布kxxk1122＜＜＜kxkxk11223＜＜＜＜在()kk12，内有且仅有一个根图像充要条件fkfkkbak()()12120020＞＞＜＜＞fkfkfk()()()1230000＞＜＞＞fkfkbakk()()()1212002·＜，或且因此，讨论二次函数在闭区间上的最值要抓住顶点的横坐标和二次函数的单调性进行处理。三、幂指、对数式1.根式式子an叫做根式，这里n叫做根指数，a叫做被开方数。根式的性质：①n为任意正整数。()aann②当n为奇数时aan，当n为偶数时aann||2.分数指数幂正分数指数幂的意义是aaamnNnmnmn()＞，、且＞01。负分数指数幂的意义是：aaamnNnmnmn101()＞，、＞且3.对数①对数的定义：若aNab()＞0且a≠1)则b叫做以a为底N的对数，记作bNalog②对数的性质几个恒等式（MN，a、b都是正数，且a，b≠1）①aNaNlog②logaNaNWww.chinaedu.com0003期版权所有不得复制2③logloglogabbNNa④loglogabba1⑤loglogambnmbna3.对数的运算法则①log()loglogaaaMNMN②logloglogaaaMNMN③logloganaMnM④logloganaMnM1例1.（1999全国，3）若函数yfx()的反函数是ygxfabab()()、、≠0，则gb()等于（）A.aB.a1C.bD.b1解：由已知点（a、b）在函数yfx()的图象上，又由反函数与原函数的性质知（b、a）在其反函数ygx()图象上，即gba()，故选A说明：本题主要考查反函数性质的运用。另：本题还可以取特殊点，特殊函数加以验证解决。例2.（2000春，北京安徽文，19）已知二次函数fxxx()()lgalga224的最大值为3，求a的值。解：原函数式可化为fx()lgallgalga(x+1ga)214由已知fx()有最大值3，所以lga＜0，并且...