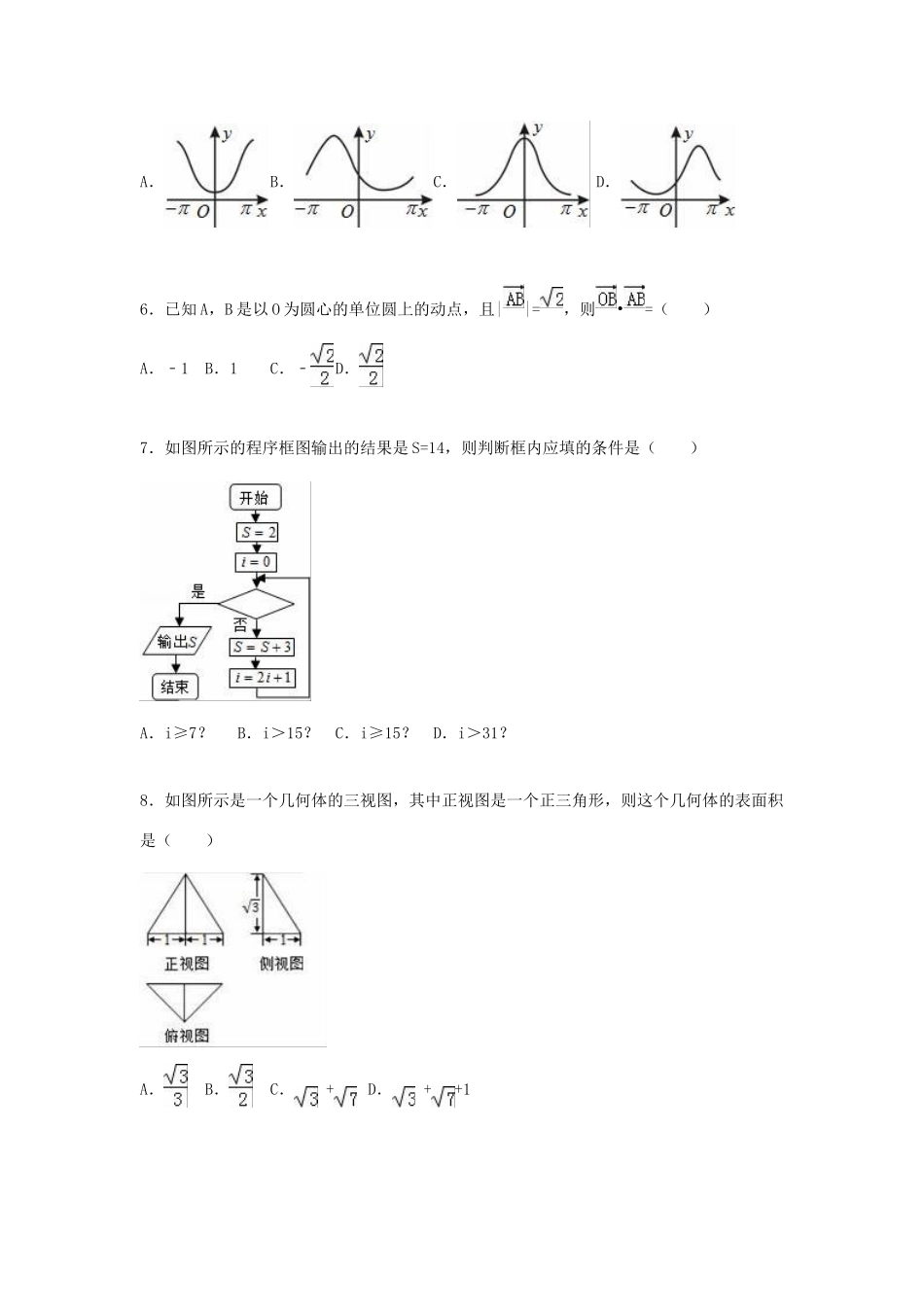
2015年福建省龙岩市高考数学一模试卷(文科)一、选择题(本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.)1.如图,设全集U=R,M={x|x>2},N={0,1,2,3},则图中阴影部分所表示的集合是()A.{3}B.{0,1}C.{0,1,2}D.{0,1,2,3}2.若命题p:∃x0∈R,sinx0=1;命题q:∀x∈R,x2+1<0,则下列结论正确的是()A.¬p为假命题B.¬q为假命题C.p∨q为假命题D.p∧q真命题3.已知函数f(x)=,则f(0)=()A.﹣1B.0C.1D.34.如图是某工厂对一批新产品长度(单位:mm)检测结果的频率分布直方图.估计这批产品的中位数为()A.20B.25C.22.5D.22.755.函数y=ecosx(﹣π≤x≤π)的大致图象为()A.B.C.D.6.已知A,B是以O为圆心的单位圆上的动点,且||=,则•=()A.﹣1B.1C.﹣D.7.如图所示的程序框图输出的结果是S=14,则判断框内应填的条件是()A.i≥7?B.i>15?C.i≥15?D.i>31?8.如图所示是一个几何体的三视图,其中正视图是一个正三角形,则这个几何体的表面积是()A.B.C.+D.++19.已知x,y满足,且目标函数z=2x+y的最小值为1,则实数a的值是()A.1B.C.D.10.已知双曲线﹣=1(a>0,b>0)的渐近线与圆(x﹣2)2+y2=1相切,则双曲线的离心率为()A.B.C.D.11.已知函数f(x)=Asin(ωx﹣)(A>0,ω>0)的部分图象如图所示,△EFG是边长为2的等边三角形,为了得到g(x)=Asinωx的图象,只需将f(x)的图象()A.向左平移个长度单位B.向右平移个长度单位C.向左平移个长度单位D.向右平移个长度单位12.如图,已知正方体ABCD﹣A1B1C1D1的棱长为4,点E,F分别是线段AB,C1D1上的动点,点P是上底面A1B1C1D1内一动点,且满足点P到点F的距离等于点P到平面ABB1A1的距离,则当点P运动时,PE的最小值是()A.5B.4C.4D.2二、填空题(本大题共4小题,每小题4分,共16分,把答案填在答题卡的相应位置上.)13.已知i是虚数单位,复数的模为.14.如图,在平行四边形ABCD中,点E在边CD上,若在平行四边形ABCD内部随机取一个点Q,则点Q取自△ABE内部的概率是.15.在△ABC中,已知=2,b=2a,那么cosB的值是.16.定义:分子为1且分母为正整数的分数叫做单位分数.我们可以把1拆分为无穷多个不同的单位分数之和.例如:1=++,1=+++,1=++++,…依此方法可得:1=++++++++++++,其中m,n∈N*,则m+n=.三、解答题(本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.)17.已知等差数列{an}的前n项和为Sn,公差d≠0,S2=4,且a2,a5,a14成等比数列.(Ⅰ)求数列{an}的通项公式;(Ⅱ)从数列{an}中依次取出第2项,第4项,第8项,…,第2n项,…,按原来顺序组成一个新数列{bn},记该数列的前n项和为Tn,求Tn的表达式.18.如图,平面ABB1A1为圆柱OO1的轴截面,点C为底面圆周上异于A,B的任意一点.(Ⅰ)求证:BC⊥平面A1AC;(Ⅱ)若D为AC的中点,求证:A1D∥平面O1BC.19.某校高一数学兴趣小组开展竞赛前摸底考试.甲、乙两人参加了5次考试,成绩如下:第一次第二次第三次第四次第五次甲的成绩8287868090乙的成绩7590917495(Ⅰ)若从甲、乙两人中选出1人参加比赛,你认为选谁合适?写出你认为合适的人选并说明理由;(Ⅱ)若同一次考试成绩之差的绝对值不超过5分,则称该次考试两人“水平相当”.由上述5次摸底考试成绩统计,任意抽查两次摸底考试,求恰有一次摸底考试两人“水平相当”的概率.20.若函数f(x)=sinωxcosωx+sin2ωx﹣(ω>0)的图象与直线y=m(m为常数)相切,并且切点的横坐标依次构成公差为π的等差数列.(Ⅰ)求ω及m的值;(Ⅱ)求函数y=f(x)在x∈[0,2π]上所有零点的和.21.已知椭圆C1:+x2=1(a>1)与抛物线C:x2=4y有相同焦点F1.(Ⅰ)求椭圆C1的标准方程;(Ⅱ)已知直线l1过椭圆C1的另一焦点F2,且与抛物线C2相切于第一象限的点A,设平行l1的直线l交椭圆C1于B,C两点,当△OBC面积最大时,求直线l的方程.22.已知函数f(x)=x3+ax+2.(Ⅰ)求证:曲线=f(x)在点(1,f(1))处的切线在y轴上的截距为定值;(Ⅱ)若x≥0时...