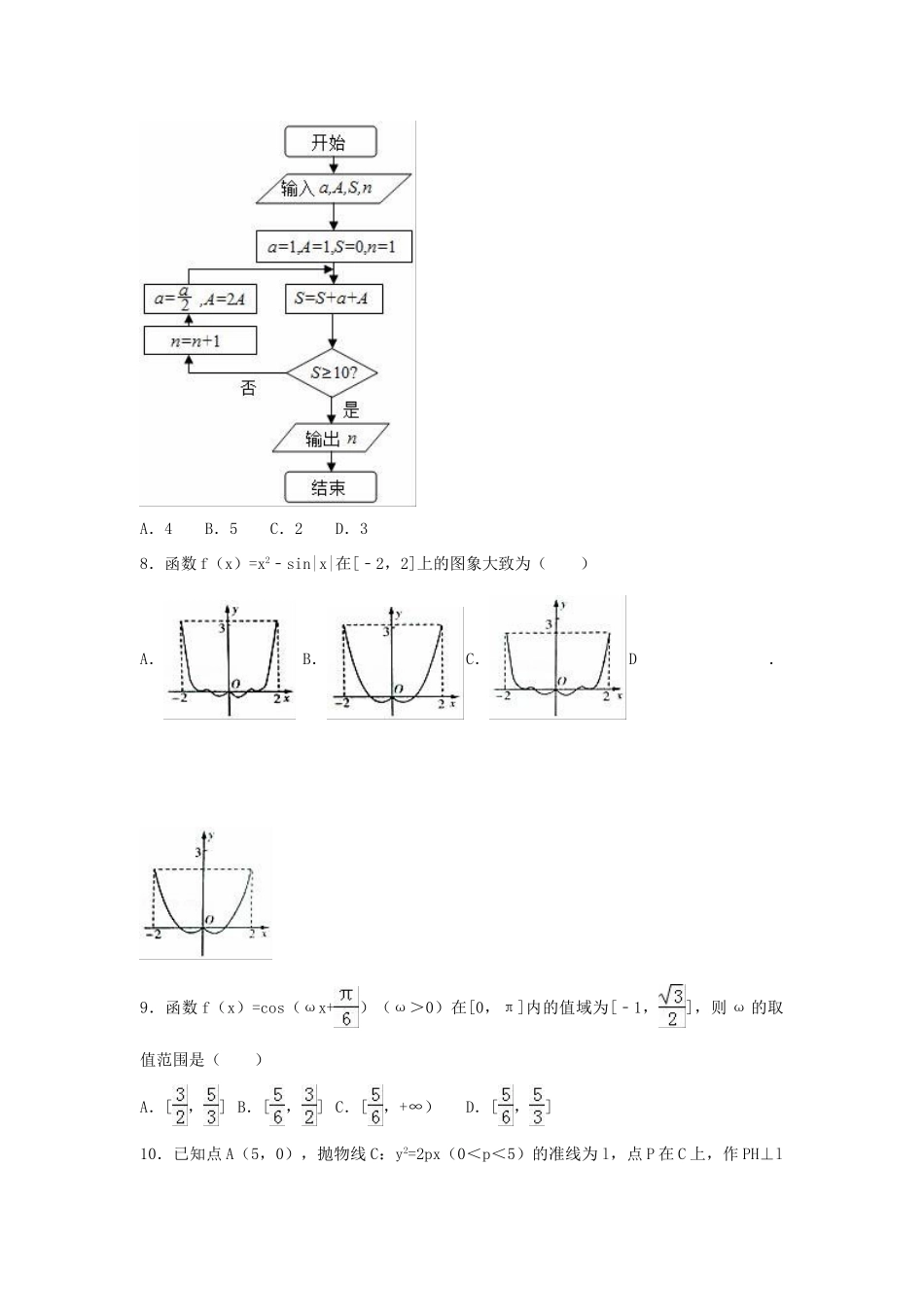
2017年福建省莆田市高考数学考前最后一卷(理科)一、选择题(本大题共有12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题意)1.已知集合A={x∈N|x≤1},B={x|x2﹣x﹣2≤0},则A∩B=()A.{0,1}B.{﹣1,0,1}C.[﹣1,1]D.{1}2.若复数z满足z2=﹣4,则||=()A.B.3C.D.53.一批产品次品率为4%,正品中一等品率为75%.现从这批产品中任取一件,恰好取到一等品的概率为()A.0.75B.0.71C.0.72D.0.34.公差不为0的等差数列{an}的前n项和为Sn,若a6=3a4,且S10=λa4,则λ的值为()A.15B.21C.23D.255.已知双曲线=1的一条渐近线斜率大于1,则实数m的取值范围()A.(0,4)B.(0,)C.(0,2)D.(,4)6.某几何体的三视图如图所示,则该几何体的表面积为()A.B.C.24﹣πD.24+π7.我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述如图所示,则输出结果n=()A.4B.5C.2D.38.函数f(x)=x2﹣sin|x|在[﹣2,2]上的图象大致为()A.B.C.D.9.函数f(x)=cos(ωx+)(ω>0)在[0,π]内的值域为[﹣1,],则ω的取值范围是()A.[,]B.[,]C.[,+∞)D.[,]10.已知点A(5,0),抛物线C:y2=2px(0<p<5)的准线为l,点P在C上,作PH⊥l于H,且|PH|=|PA|,∠APH=120°,则p=()A.1B.2C.3D.411.正方体ABCD﹣A1B1C1D1的棱长为6,点O在BC上,且BO=OC,过点O的直线l与直线AA1,C1D1分别交于M,N两点,则MN与面ADD1A1所成角的正弦值为()A.B.C.D.12.已知直线l1:y=x+a分别与直线l2:y=2(x+1)及曲线C:y=x+lnx交于A,B两点,则A,B两点间距离的最小值为()A.B.3C.D.3二、填空题(本大题共有4个小题,每题5分,共20分)13.设变量x,y满足约束条件,则z=x﹣2y的最大值为.14.已知=(,),||=1,|+2|=2,则在方向上的投影为.15.(x+1)4展开式中不含x2项的系数之和为.16.数列{an}的前n项和为Sn,且S3=1,S4=﹣3,an+3=2an(n∈N*),则S2017=.三、解答题(本大题共6个小题,共70分,解答时要求写出必要的文字说明或推演步骤.请按照题目顺序在第Ⅱ卷各个题目的答题区域内作答.)17.(12分)如图,在△ABC中,∠B=,D为边BC上的点,E为AD上的点,且AE=8,AC=4,∠CED=.(1)求CE的长(2)若CD=5,求cos∠DAB的值.18.(12分)如图所示,在三棱柱ABC﹣A1B1C1中,AA1B1B为正方形,BB1C1C为菱形,B1C⊥AC1.(Ⅰ)求证:平面AA1B1B⊥平面BB1C1C;(Ⅱ)若D是CC1中点,∠ADB是二面角A﹣CC1﹣B的平面角,求直线AC1与平面ABC所成角的余弦值.19.(12分)某早餐店每天制作甲、乙两种口味的糕点共n(n∈N*)份,每份糕点的成本1元,售价2元,如果当天卖不完,剩下的糕点作废品处理,该早餐店发现这两种糕点每天都有剩余,为此整理了过往100天这两种糕点的日销量(单位:份),得到如下统计数据:甲口味糕点日销量48495051天数20402020乙口味糕点日销量48495051天数40302010以这100天记录的各销量的频率作为各销量的概率,假设这两种糕点的日销量相互独立.(1)记该店这两种糕点每日的总销量为X份,求X的分布列;(2)早餐店为了减少浪费,提升利润,决定调整每天制作糕点的份数.①若产生浪费的概率不超过0.6,求n的最大值;②以销售这两种糕点的日总利润的期望值为决策依据,在每天所制糕点能全部卖完与n=98之中选其一,应选哪个?20.(12分)已知圆F1:(x+1)2+y2=16,定点F2(1,0),A是圆F1上的一动点,线段F2A的垂直平分线交半径F1A于P点.(Ⅰ)求P点的轨迹C的方程;(Ⅱ)四边形EFGH的四个顶点都在曲线C上,且对角线EG,FH过原点O,若kEG•kFH=﹣,求证:四边形EFGH的面积为定值,并求出此定值.21.(12分)已知函数f(x)=(x﹣3)ex+ax,a∈R.(Ⅰ)当a=1时,求曲线f(x)在点(2,f(2))处的切线方程;(Ⅱ)当a∈[0,e)时,设函数f(x)在(1,+∞)上的最小值为g(a),求函数g(a)的值域.[选修4-4:坐标系与参数方程]22.(10分)点P是曲线C1:(x﹣2)2+y2=4上的...