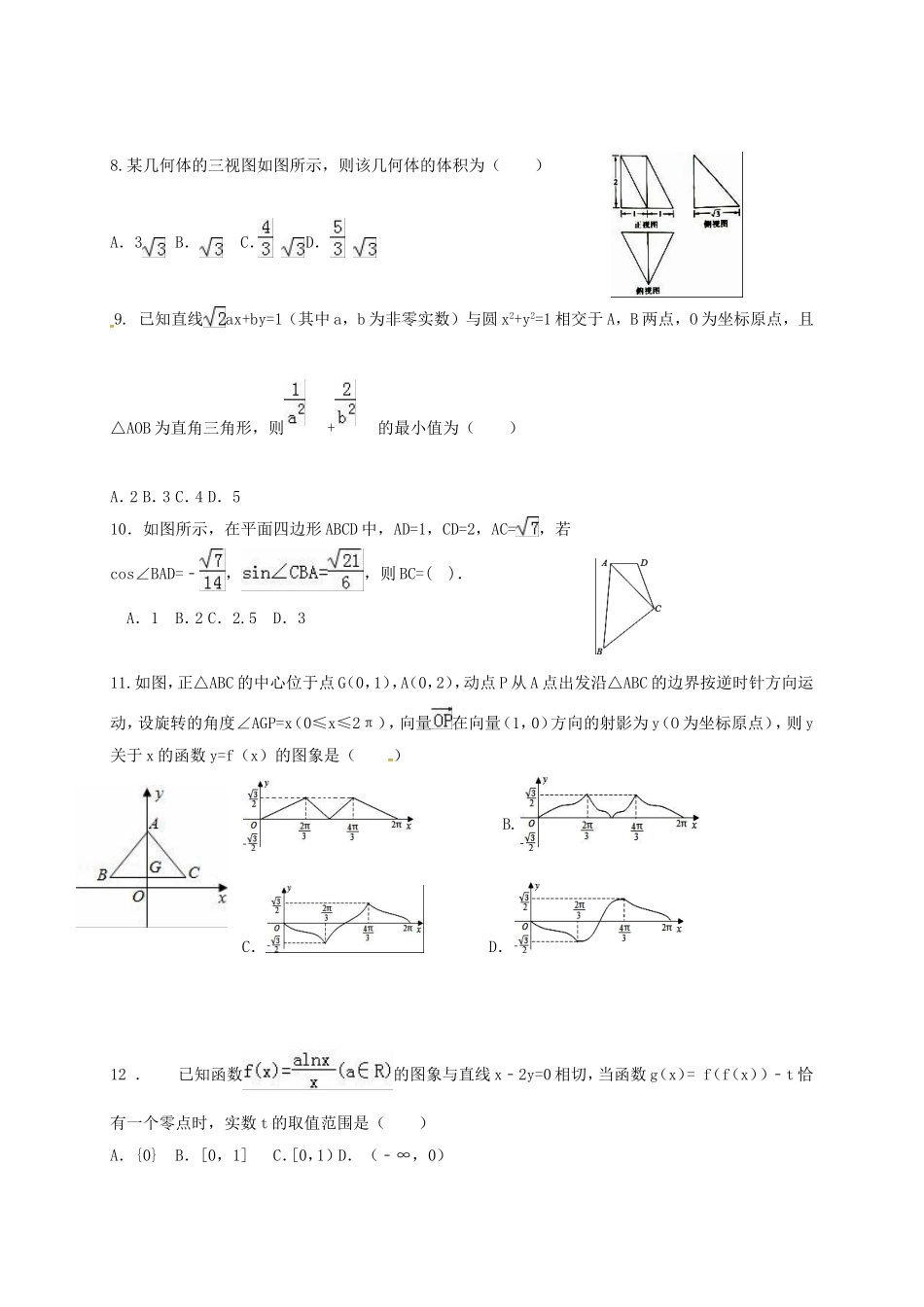
福建省莆田市2017届高三数学考前模拟(最后一卷)试题文一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知全集U=R,集合A={x|2x<1},B={x|log3x>0},则A∩(∁UB)=()A.{x|x>1}B.{x|x>0}C.{x|0<x<1}D.{x|x<0}2.已知i是虚数单位,复数z满足(i﹣1)z=i,则z的虚部是()A.B.C.D.3.已知实数{an}是等比数列,若a2a5a8=8,则a1a9+a1a5+a5a9()A.有最小值12B.有最大值12C.有最小值4D.有最大值44.方程lnx+2x=6的根所在的区间为()A.(2,2.25)B.(2.25,2.5)C.(2.5,2.75)D.(2.75,3)5.已知双曲线:的左、右焦点与虚轴的一个端点构成一个角为的三角形,则双曲线的离心率为()A.B.C.3D.56.我们知道,“心有灵犀”一般是对人的心理活动非常融洽的一种描述,它也可以用数学来定义:甲、乙两人都在中说一个数,甲说的数记为,乙说的数记为,若,则称甲、乙两人“心有灵犀”,由此可以得到甲、乙两人“心有灵犀”的概率是()A.B.C.D.7.如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b的值分别是21,28,则输出a的值为()A.14B.7C.1D.08.某几何体的三视图如图所示,则该几何体的体积为()A.3B.C.D.9.已知直线ax+by=1(其中a,b为非零实数)与圆x2+y2=1相交于A,B两点,O为坐标原点,且△AOB为直角三角形,则+的最小值为()A.2B.3C.4D.510.如图所示,在平面四边形ABCD中,AD=1,CD=2,AC=,若cos∠BAD=﹣,,则BC=().A.1B.2C.2.5D.311.如图,正△ABC的中心位于点G(0,1),A(0,2),动点P从A点出发沿△ABC的边界按逆时针方向运动,设旋转的角度∠AGP=x(0≤x≤2π),向量在向量(1,0)方向的射影为y(O为坐标原点),则y关于x的函数y=f(x)的图象是()B.C.D.12.已知函数的图象与直线x﹣2y=0相切,当函数g(x)=f(f(x))﹣t恰有一个零点时,实数t的取值范围是()A.{0}B.[0,1]C.[0,1)D.(﹣∞,0)二、填空题:本大题共4小题,每小题5分.13.已知,若则.14.已知tanα,tanβ分别是lg(6x2﹣5x+2)=0的两个实根,则tan(α+β)=.15.若实数满足条件,则.16.点为正方体的内切球球面上的动点,点为上一点,,,若球的体积为,则动点的轨迹的长度为.三、解答题:第17~21题每题12分,解答应在答卷的相应各题中写出文字说明,说明过程或演算步骤.17.(本小题满分12分)数列{an}满足a1=1,(n∈N+).(1)证明:数列是等差数列;(2)求数列{an}的通项公式an;(3)设bn=n(n+1)an,求数列{bn}的前n项和Sn.18、(本小题满分12分)某商店经营某种特殊商品,商店每销售一件该商品可获利3元,若每周进货量供大于求,剩余商品削价处理,每处理一件商品亏损1元;若每周供不应求,则可以从外部调剂供应,此时每件商品仅获利2元.为了了解市场需求的情况,经销商统计了去年一年(52周)的销售情况.以去年每周的销售量的频率为今年每周市场需求量的概率.(1)要使进货量不超过市场需求量的概率大于0.5,问进货量的最大值是多少?(2)如果今年的周进货量为14,平均来说今年每周的利润是多少?19.(本小题满分12分)如图,在三棱锥中,,平面平面,点D,分别为的中点.(1)证明:平面;(2)设点为线段的中点,且平面,求三棱锥的体积.20.(本小题满分12分)已知曲线C上任一点到点和直线:的距离相等,圆D:。(Ⅰ)求曲线C的方程;(Ⅱ)过点作曲线C的切线,并与圆D相切,求半径r;(Ⅲ)若曲线C与圆D恰有一个公共点,且在点处两曲线的切线为同一直线,求半径r。这时,你认为曲线C与圆D共有几条公切线(不必证明)?(注:公切线是与两曲线都相切的直线,切点可以不同。)21.(本小题满分12分)设函数(Ⅰ)当时,求函数的零点;(Ⅱ)当时,讨论函数的单调性;(Ⅲ)在(Ⅱ)条件下,若有两个极值点是,过点的直线的斜率为,问:是否存在,使?若存在,求出的值;若不存在,请说明理由。请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.(本小题满分10分)已知曲线...