福建省四地六校高一数学下学期第二次月考试卷（解析（含解析）-人教版高一全册数学试题VIP专享VIP免费

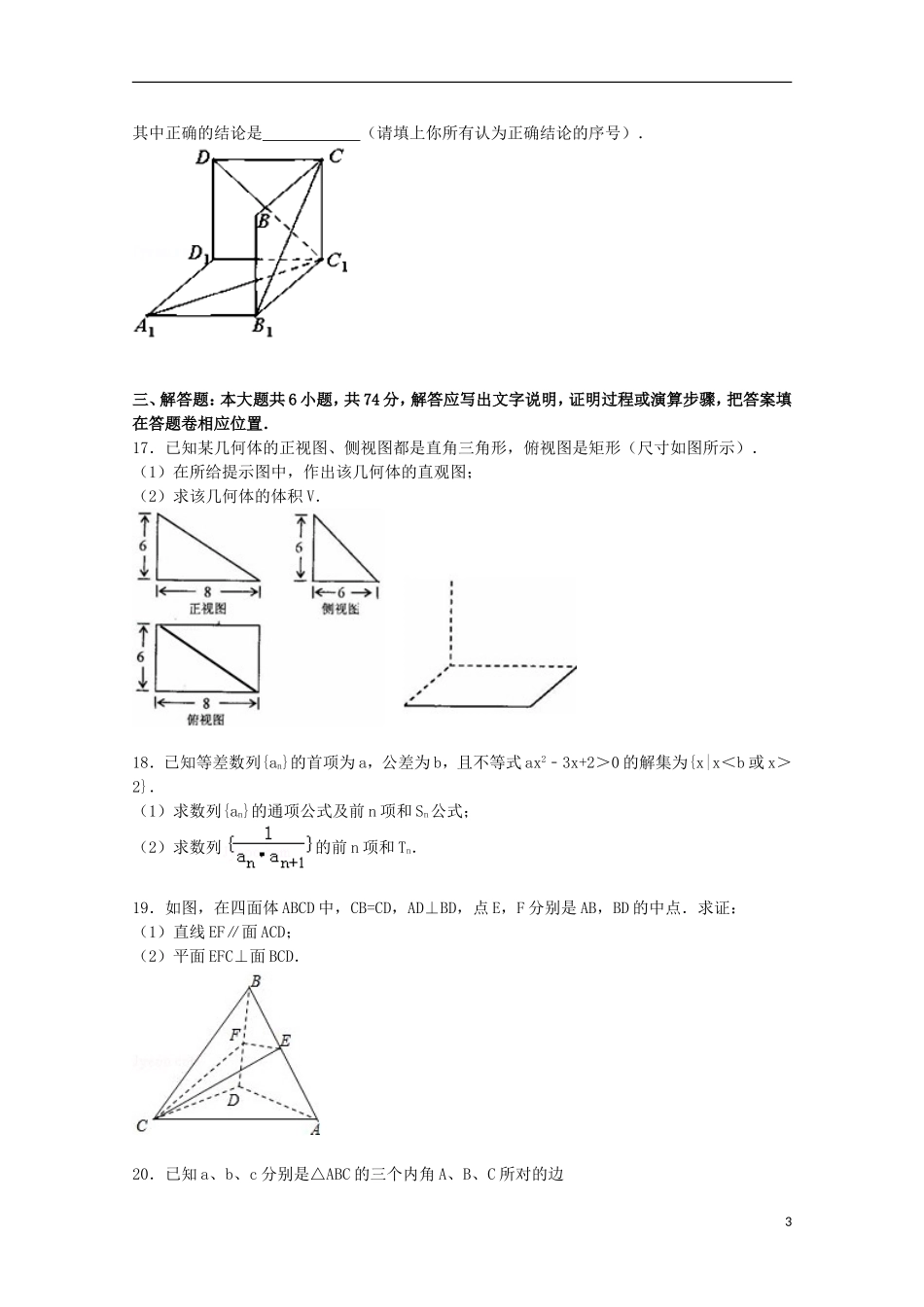
2014-2015学年福建省四地六校高一（下）第二次月考数学试卷一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知a＞b＞0，那么下列不等式成立的是（）A．﹣a＞﹣bB．a+c＜b+cC．a2＞b2D．＞2．若直线l∥平面α，直线a⊆α，则l与a的位置关系是（）A．l∥aB．l与a异面C．l与a没有公共点D．l与a相交3．在△ABC中，若A=60°，BC=4，AC=4，则角B的大小为（）A．30°B．45°C．135°D．45°或135°4．已知x，y，z∈R，若﹣1，x，y，z，﹣3成等比数列，则xyz的值为（）A．﹣3B．±3C．D．5．如图Rt△O′A′B′是一平面图形的直观图，斜边O′B′=2，则这个平面图形的面积是（）A．B．1C．D．6．点（a，b）在直线2x﹣y+3=0的右下方，则（）A．2a﹣b+3＜0B．2a﹣b+3＞0C．2a﹣b+3=0D．以上都不成立7．已知m、n为两条不同的直线，α、β为两个不同的平面，下列命题中的正确的是（）A．若α∥β，m∥α，则m∥βB．若m∥α，m⊥n，则n⊥αC．若α⊥β，m⊥β，则m⊥αD．若m⊥α，m⊥β，则α∥β8．下列结论正确的是（）A．当时，B．当x＞0时，C．当x≥2时，的最小值为2D．当0＜x≤2时，无最大值9．如图，正方体ABCD﹣A1B1C1D1中，E，F分别为棱AB，CC1的中点，在平面ADD1A1内且与平面D1EF平行的直线（）1A．不存在B．有1条C．有2条D．有无数条10．已知数列{2n﹣（﹣1）n}的前10项和为（）A．210﹣3B．210﹣2C．211﹣3D．211﹣211．如图，要测量底部不能到达的某铁塔AB的高度，在塔的同一侧选择C、D两观测点，且在C、D两点测得塔顶的仰角分别为45°、30°．在水平面上测得∠BCD=120°，C、D两地相距600m，则铁塔AB的高度是（）A．120mB．480mC．240mD．600m12．正数x、y满足，若x+2y＞m2+2m恒成立，则实数m的取值范围是（）A．m≤﹣2或m≥4B．m≤﹣4或m≥2C．﹣2＜m＜4D．﹣4＜m＜2二、填空题（本题共4小题，每小题4分，共16分，在答题卷上的相应题目的答题区域内作答．）13．已知0＜x＜1，﹣1＜y＜1，则x﹣y的取值范围是．14．球的表面积为16πcm2，则球的体积为cm3．15．数列{an}中a1=1，an+1=an+n，则a10=．16．如图是从上下底面处在水平状态下的棱长为a的正方体ABCD﹣A1B1C1D1中分离出来的．有如下结论：①∠DC1D1在图中的度数和它表示的角的真实度数都是45°；②∠A1C1D=∠A1C1D1+∠D1C1D；③A1C1与BC1所成的角是30°；④若BC=m，则用图示中这样一个装置盛水，最多能盛的水．2其中正确的结论是（请填上你所有认为正确结论的序号）．三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤，把答案填在答题卷相应位置．17．已知某几何体的正视图、侧视图都是直角三角形，俯视图是矩形（尺寸如图所示）．（1）在所给提示图中，作出该几何体的直观图；（2）求该几何体的体积V．18．已知等差数列{an}的首项为a，公差为b，且不等式ax2﹣3x+2＞0的解集为{x|x＜b或x＞2}．（1）求数列{an}的通项公式及前n项和Sn公式；（2）求数列的前n项和Tn．19．如图，在四面体ABCD中，CB=CD，AD⊥BD，点E，F分别是AB，BD的中点．求证：（1）直线EF∥面ACD；（2）平面EFC⊥面BCD．20．已知a、b、c分别是△ABC的三个内角A、B、C所对的边3（1）若，试判断△ABC的形状．（2）若cos2A+3cosA=1，a=，求△ABC面积的最大值．21．如图，设计一个小型正四棱锥形冷水塔，其中顶点P在底面的射影为正方形ABCD的中心O，返水口E为BC的中点，冷水塔的四条钢梁（侧棱）设计长度均为10米．冷水塔的侧面选用钢板，基于安全与冷凝速度的考量，要求钢梁（侧棱）与底面的夹角α落在区间内，如何设计可得侧面钢板用料最省且符合施工要求？22．已知函数．（Ⅰ）求f（x）+f（1﹣x），x∈R的值；（Ⅱ）若数列{an}满足an=f（0）+f（）+f（）+…+f（）+f（1）（n∈N*），求数列{an}的通项公式；（Ⅲ）若数列{bn}满足bn=2n+1an，Sn是数列{bn}的前n项和，是否存在正实数k，使不等式knSn＞4bn对于一切的n∈N*恒成立？若存在，请求出k的取值范围；若不存在，请说明理由．42014-2015学年福建省四地六校高一（下）第二次月考数学试卷参考答案与试题解析一、选择题...