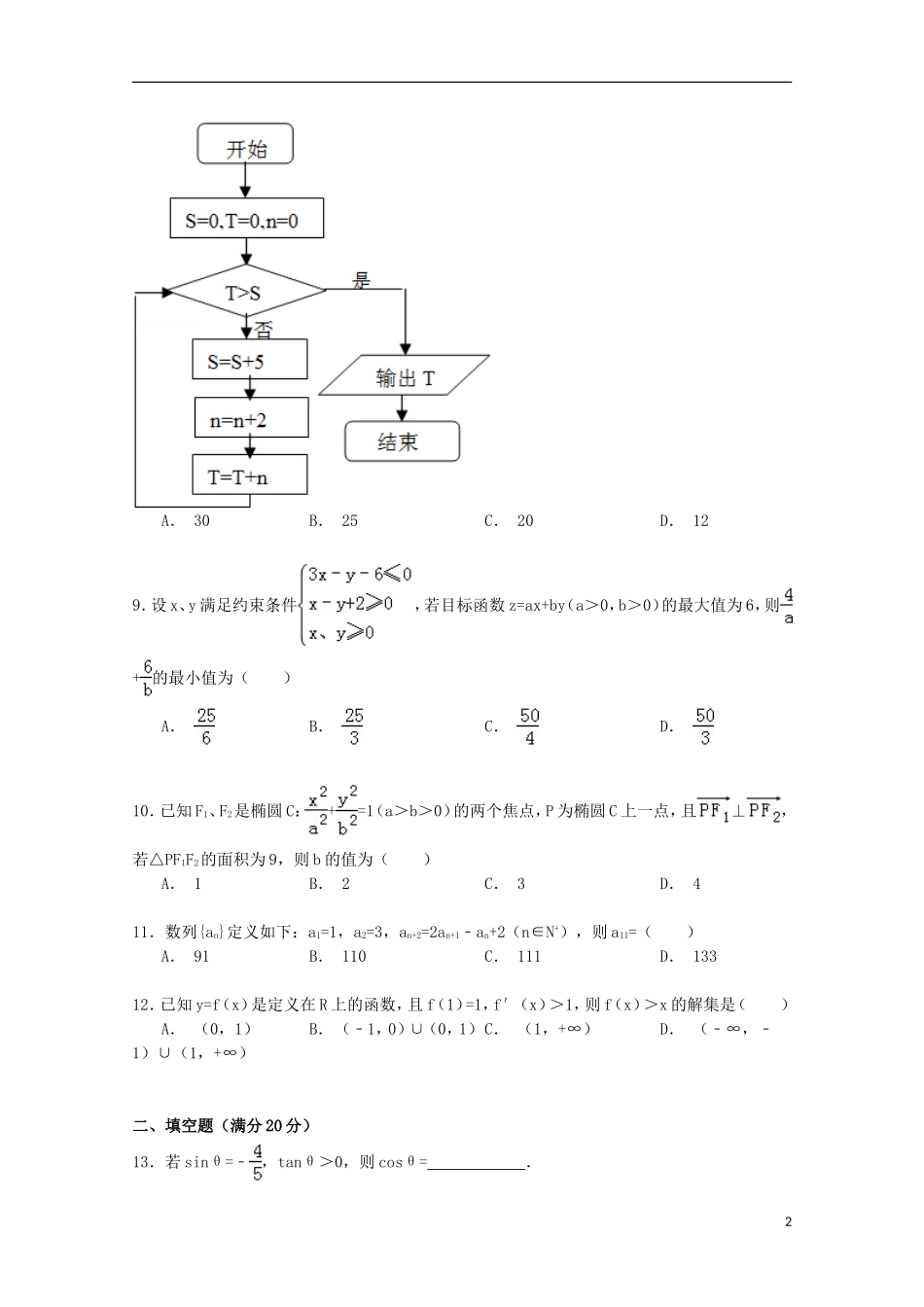
甘肃省张掖二中2014-2015学年高三(下)5月月考数学试卷(理科)一、选择题(满分60分)1.若A={x|x2=1},B={x|x2﹣2x﹣3=0},则A∩B=()A.3B.1C.∅D.﹣12.若复数z满足iz=2+4i,则在复平面内,z对应的点的坐标是()A.(2,4)B.(2,﹣4)C.(4,﹣2)D.(4,2)3.已知点A(1,1),B(4,2)和向量=(2,λ),若∥,则实数λ的值为()A.﹣B.C.D.﹣4.把分别标有“A”“B”“C”的三张卡片随意的排成一排,则能使卡片从左到右可以念成“ABC”和“CBA”的概率是()A.B.C.D.5.在△ABC中,若∠A=,,则的值为()A.B.C.D.6.如图,格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体最长的棱的长度等于()A.B.C.5D.27.正三棱柱ABC﹣A1B1C1的底面边长为2,侧棱长为,D为BC中点,则三棱锥A﹣B1DC1的体积为()A.3B.C.1D.8.执行如图的程序框图,输出的T=()1A.30B.25C.20D.129.设x、y满足约束条件,若目标函数z=ax+by(a>0,b>0)的最大值为6,则+的最小值为()A.B.C.D.10.已知F1、F2是椭圆C:+=1(a>b>0)的两个焦点,P为椭圆C上一点,且⊥,若△PF1F2的面积为9,则b的值为()A.1B.2C.3D.411.数列{an}定义如下:a1=1,a2=3,an+2=2an+1﹣an+2(n∈N+),则a11=()A.91B.110C.111D.13312.已知y=f(x)是定义在R上的函数,且f(1)=1,f′(x)>1,则f(x)>x的解集是()A.(0,1)B.(﹣1,0)∪(0,1)C.(1,+∞)D.(﹣∞,﹣1)∪(1,+∞)二、填空题(满分20分)13.若sinθ=﹣,tanθ>0,则cosθ=.214.过抛物线y2=8x的焦点作倾斜角为直线l,直线l与抛物线相交与A,B两点,则弦|AB|的长是.15.图中阴影部分的面积等于.16.定义在R上的函数f(x)满足:f(x+2)+f(x)=0,且函数f(x+1)为奇函数,对于下列命题:①函数f(x)满足f(x+4)=f(x);②函数f(x)图象关于点(1,0)对称;③函数f(x)的图象关于直线x=2对称;④函数f(x)的最大值为f(2);⑤f(2009)=0.其中正确的序号为.三、解答题17.设数列{an}是首项为1,公差为d的等差数列,且a1,a2﹣1,a3﹣1是等比数列{bn}的前三项.(Ⅰ)求{an}的通项公式;(Ⅱ)求数列{bn}的前n项和Tn.18.平行四边形ABCD中,AB=2,AD=2,且∠BAD=45°,以BD为折线,把△ABD折起,使平面ABD⊥平面CBD,连AC.(Ⅰ)求证:AB⊥DC(Ⅱ)求二面角B﹣AC﹣D平面角的大小;(Ⅲ)求四面体ABCD外接球的体积.19.某校兴趣小组进行了一项“娱乐与年龄关系”的调查,对15~65岁的人群随机抽取1000人的样本,进行了一次“是否是电影明星追星族”调查,得到如下各年龄段样本人数频率分布直方图和“追星族”统计表:“追星族”统计表3组数分组“追星族”人数占本组频率一20.1(1)求a,b的值.(2)设从45岁到65岁的人群中,随机抽取2人,用样本数据估计总体,ξ表示其中“追星族”的人数,求ξ分布列、期望和方差.20.已知离心率为的椭圆上的点到左焦点F的最长距离为.(1)求椭圆的方程;(2)如图,过椭圆的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”,求椭圆的“左特征点”M的坐标.21.已知函数f(x)=ex﹣ax﹣1(a>0,e为自然对数的底数)(1)求函数f(x)的最小值;(2)若f(x)≥0对任意的x∈R恒成立,求实数a的值;(3)在(2)的条件下,证明:1+++…+>ln(n+1)(n∈N*)三.请从下面所给的22、23、24三题中选定一题作答,并用2B铅笔在答题卡上将所选题目对应的题号方框涂黑,按所涂题号进行评分;不涂、多图均按所答第一题评分;多答按所答第一题评分.22.如图,AB是⊙O的直径,弦CD与AB垂直,并与AB相交于点E,点F为弦CD上异于点E的任意一点,连接BF、AF并延长交⊙O于点M、N.4(1)求证:B、E、F、N四点共圆;(2)求证:AC2+BF•BM=AB2.23.(2015•张掖一模)选修4﹣4:坐标系与参数方程极坐标系与直角坐标系xOy有相同的长度单位,以原点O为极点,以x轴正半轴为极轴.已知直线l的参数方程为,(t为参数),曲线C的极坐标方程为ρsi...