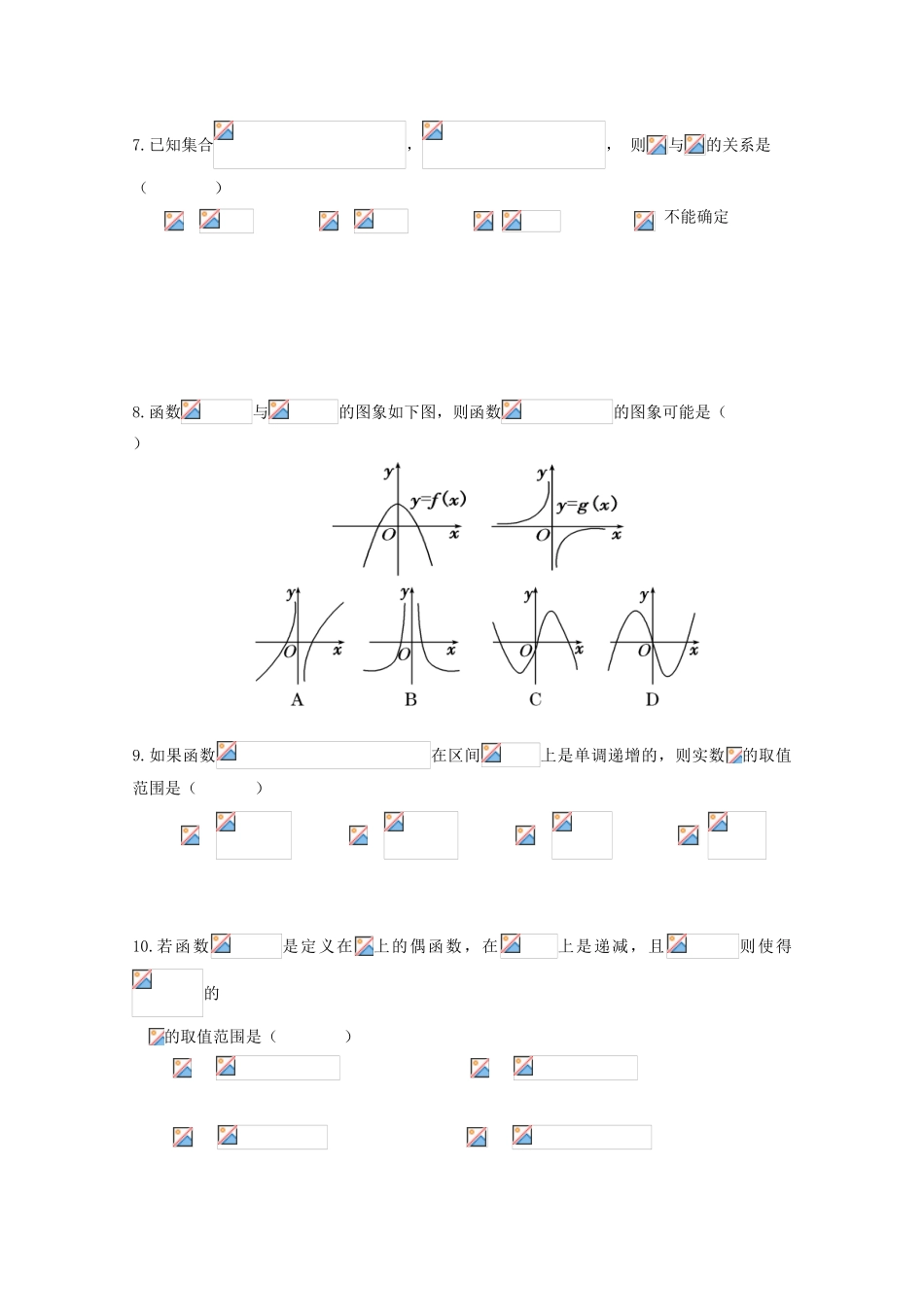
安徽省合肥市2017-2018学年高一数学10月月考试题(考试时间:120分钟试卷分值:150分)一、选择题(每题5分,共60分)1.已知集合,,则集合中元素的个数为()2.设集合,若是集合到集合的映射,则集合可以是()3.下列四组中的,,表示同一个函数的是()4.下列函数在其定义域内既是奇函数又是增函数的为()5.已知函数则()6.给出函数如下表,若,则的值构成的集合为()7.已知集合,,则与的关系是()不能确定8.函数与的图象如下图,则函数的图象可能是()9.如果函数在区间上是单调递增的,则实数的取值范围是()10.若函数是定义在上的偶函数,在上是递减,且则使得的的取值范围是()11.已知函数是定义在实数集上的不恒为零的偶函数,且对任意实数都有则的值是()12.已知函数.设关于的不等式的解集为,若,则实数的取值范围是()二、填空题(每题5分,共20分)13.函数的定义域是___________.14.已知函数为偶函数,则_____________.15.函数的单调递减区间是___________.16.已知函数在上为奇函数,当时,,则______________.三、解答题(共6题,共70分)17.(10分)设,,,求:(1);(2).18.(12分)已知集合,(1)若,求,的值;(2)若,求实数,满足的条件.19.(12分)已知函数,(1)证明在上单调递减;(2)求在上的值域.20.(12分)某公司需将一批货物从甲地运到乙地,现有汽车、火车两种运输工具可供选择.若该货物在运输过程中(含装卸时间)的损耗为300元/小时,其他主要参考数据如下:运输工具途中速度(千米/小时)途中费用(元/千米)装卸时间(小时)装卸费用(元)汽车50821000火车100441800若甲地与乙地的距离的取值范围为,则选择哪种运输工具更合算.21.(12分)已知定义在上的函数同时满足下列三个条件:①;②对任意都有;③.(1)求、的值;(2)证明:函数在上为减函数;(3)解关于的不等式.22.(12分)已知二次函数满足条件:,且方程有两个相等实根.(1)求的解析式;(2)是否存在实数,使的定义域和值域分别为和?如存在,求出的值;如不存在,说明理由.第一次段考数学参考答案1—56—1011—1213.14.–115.(也可以写成)16.17.(1);(3分)(2)(6分)18.(1)方程有两个相等的根.(1分)即(4分)(2),(6分)即,实数,满足的条件为,.(8分)19.(1),设则(2分)即在上单调递减(4分)(2)由(1)可知在上单调递减(5分)同理可得在上单调递减(6分)在上的值域为(8分)20.设甲、乙两地距离为千米(),选用汽车、火车运输时的总支出分别为和.由题意得两种工具在运输过程中(含装卸)的费用与时间如下表:运输工具途中及装卸费用途中时间汽车8x+1000+2火车4x+1800+4于是y1=8x+1000+(+2)×300=14x+1600,y2=4x+1800+(+4)×300=7x+3000.(5分)令y1-y2<0得x<200.①当时,y1y2,此时选用火车合算.(8分)21.(1)令,则令,则,(3分)(2),设则,令,则即,函数在上为减函数(6分)(3)解得原不等式的解集为(9分)22.(1)由得;又方程有两个相等实根,,,(3分)(2)的对称轴为,因此在上的值域为.(4分)即(6分)在上单调递增即是方程的两根,(9分)