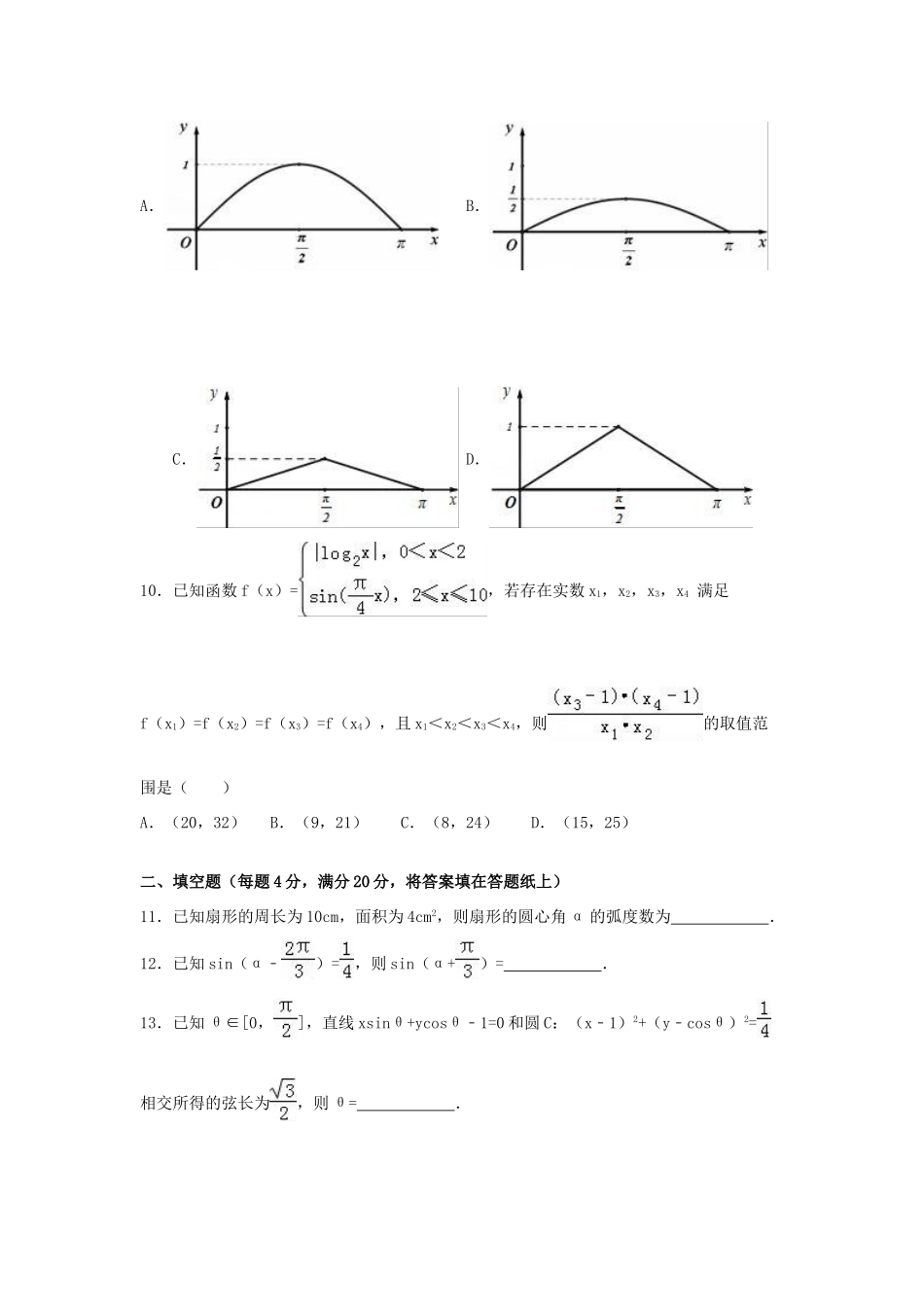
2015-2016学年安徽省六安一中高一(下)期中数学试卷一、选择题:本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.在△ABC中,若sinA,cosA是关于x的方程3x2﹣2x+m=0的两个根,则△ABC是()A.钝角三角形B.直角三角形C.锐角三角形D.不能确定2.函数y=Asin(ωx+φ)在一个周期内的图象如图,此函数的解析式为()A.y=2sin(2x+)B.y=2sin(2x+)C.y=2sin(﹣)D.y=2sin(2x﹣)3.已知非零向量,,,满足=2﹣,=k+,给出以下结论:①若与不共线,与共线,则k=﹣2;②若与不共线,与共线,则k=2;③存在实数k,使得与不共线,与共线;④不存在实数k,使得与不共线,与共线.其中正确结论的个数是()A.1个B.2个C.3个D.4个4.已知α为锐角,且有,tan(π+α)+6sin(π+β)﹣1=0,则sinα的值是()A.B.C.D.5.已知两点A(1,2),B(3,1)到直线l距离分别是,﹣,则满足条件的直线l共有()条.A.1B.2C.3D.46.(理科)已知两点A(0,﹣3),B(4,0),若点P是圆x2+y2﹣2y=0上的动点,则△ABP面积的最小值为()A.6B.C.8D.7.已知点P(x,y)是直线kx+y+4=0(k>0)上一动点,PA,PB是圆C:x2+y2﹣2y=0的两条切线,A,B是切点,若四边形PACB的最小面积是2,则k的值为()A.3B.C.D.28.函数y=sin2x+2cosx()的最大值与最小值分别为()A.最大值,最小值为﹣B.最大值为,最小值为﹣2C.最大值为2,最小值为﹣D.最大值为2,最小值为﹣29.如图,点P在半径为1的半圆上运动,AB是直径,当P沿半圆弧从A到B运动时,点P经过的路程x与△APB的面积y的函数y=f(x)的图象是下图中的()A.B.C.D.10.已知函数f(x)=,若存在实数x1,x2,x3,x4满足f(x1)=f(x2)=f(x3)=f(x4),且x1<x2<x3<x4,则的取值范围是()A.(20,32)B.(9,21)C.(8,24)D.(15,25)二、填空题(每题4分,满分20分,将答案填在答题纸上)11.已知扇形的周长为10cm,面积为4cm2,则扇形的圆心角α的弧度数为.12.已知sin(α﹣)=,则sin(α+)=.13.已知θ∈[0,],直线xsinθ+ycosθ﹣1=0和圆C:(x﹣1)2+(y﹣cosθ)2=相交所得的弦长为,则θ=.14.已知函数f(x)=sin(x+),其中x∈[﹣,α],若f(x)的值域是[﹣,1],则a的取值范围是.15.如图△ABC是直角边等于4的等腰直角三角形,D是斜边BC的中点,=+m•,向量的终点M在△ACD的内部(不含边界),则实数m的取值范围是.三、解答题(本大题共5小题,共50分.解答应写出文字说明、证明过程或演算步骤.)16.已知函数f(x)=2sin(2x﹣),x∈R.(1)在给定的平面直角坐标系中,画函数f(x)=2sin(2x﹣),x∈[0,π]的简图;(2)求f(x)=2sin(2x﹣),x∈[﹣π,0]的单调增区间;(3)函数g(x)=2cos2x的图象只经过怎样的平移变换就可得到f(x)=2sin(2x﹣),x∈R的图象?17.已知圆C:x2+(y﹣1)2=5,直线l:mx﹣y+1﹣m=0,且直线l与圆C交于A、B两点.(1)若|AB|=,求直线l的倾斜角;(2)若点P(1,1),满足2=,求直线l的方程.18.平面内有一个△ABC和一点O(如图),线段OA,OB,OC的中点分别为E,F,G,BC,CA,AB的中点分别为L,M,N,设=,=,=.(1)试用,,表示向量,,;(2)证明:线段EL,FM,GN交于一点且互相平分.19.已知:以点C(t,)(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.(Ⅰ)当t=2时,求圆C的方程;(Ⅱ)求证:△OAB的面积为定值;(Ⅲ)设直线y=﹣2x+4与圆C交于点M,N,若|OM|=|ON|,求圆C的方程.20.已知f(x)=sin2(2x﹣)﹣2t•sin(2x﹣)+t2﹣6t+1(x∈[,])其最小值为g(t).(1)求g(t)的表达式;(2)当﹣≤t≤1时,要使关于t的方程g(t)=kt有一个实根,求实数k的取值范围.2015-2016学年安徽省六安一中高一(下)期中数学试卷参考答案与试题解析一、选择题:本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.在△ABC中,若sinA,cosA是关于x的方程3x2﹣2x+m=0的两个根,则△ABC是()A.钝角三角形B.直角三角...