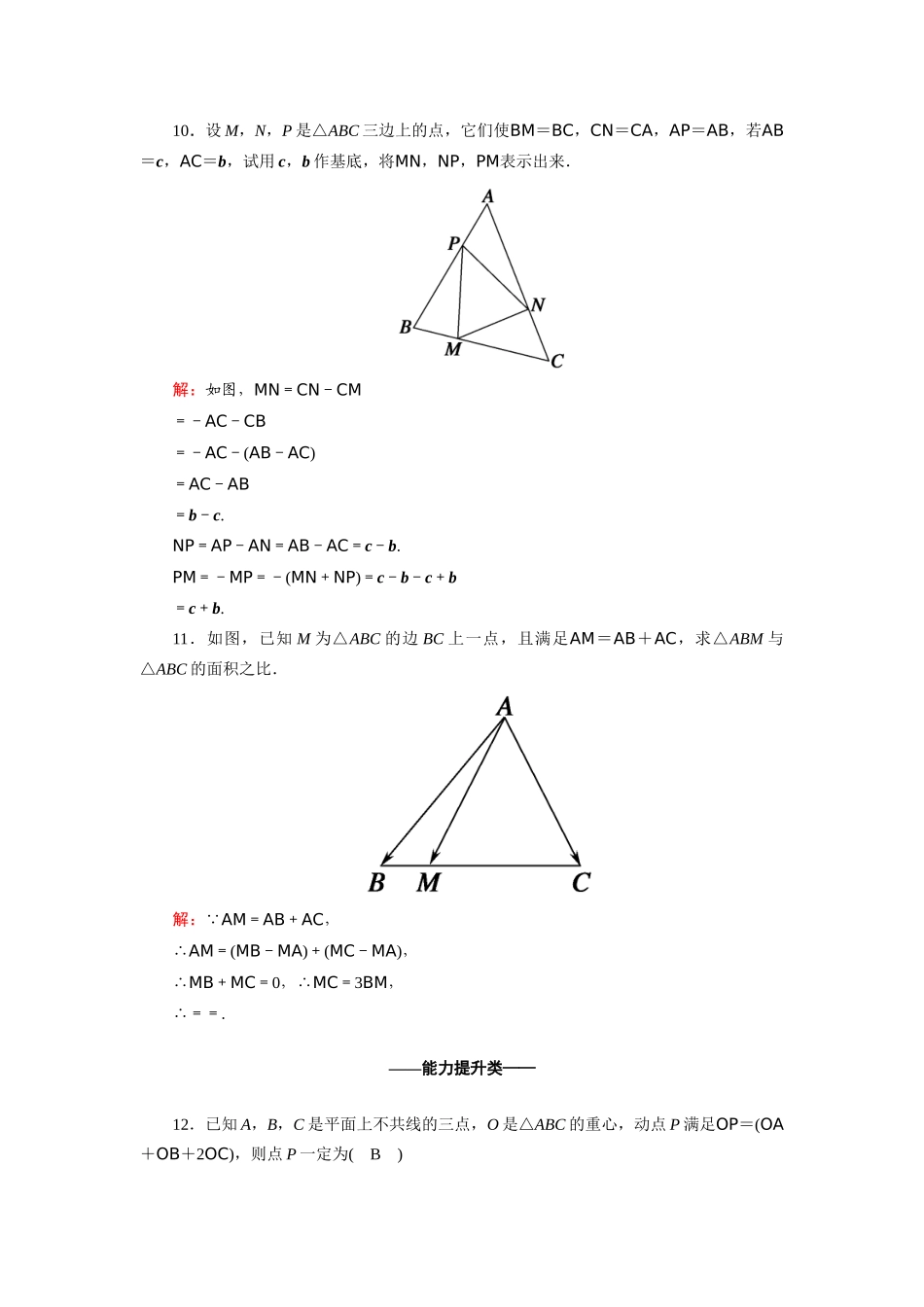
课时作业18平面向量基本定理——基础巩固类——一、选择题1.已知向量a与b的夹角为,则向量2a与-3b的夹角为(C)A.B.C.D.解析:∵a与2a同向,b与-3b反向,∴向量2a与-3b的夹角和a与b的夹角互补,∴向量2a与-3b的夹角为.2.在△ABC中,已知D为AC上一点,若AD=2DC,则BD=(D)A.-BC-BAB.BC+BAC.-BC-BAD.BC+BA解析:如图,BD=BA+AD=BA+AC=BA+(BC-BA)=BC+BA,故选D.3.已知e1,e2是平面α内两个不共线的向量,下列说法中正确的个数为(B)①λe1+μe2(λ,μ∈R)可以表示平面α内的所有向量;②对于平面α内的任一向量a,使a=λe1+μe2的实数对(λ,μ)有无穷多个;③若平面向量λ1e1+μ1e2与λ2e1+μ2e2共线,则有且只有一个实数λ,使得λ1e1+μ1e2=λ(λ2e1+μ2e2);④若存在实数λ,μ使得λe1+μe2=0,则λ=μ=0.A.1B.2C.3D.4解析:根据平面向量基本定理,易知①④正确,②③错误.故选B.4.e1,e2为基底向量,已知向量AB=e1-ke2(k∈R),CB=2e1-e2,CD=3e1-3e2,若A、B、D三点共线,则k的值是(A)A.2B.-3C.-2D.3解析:若A、B、D三点共线,则AB∥BD,设AB=tBD(t∈R),由于BD=BC+CD=e2-2e1+3e1-3e2=e1-2e2,所以e1-ke2=t(e1-2e2),又e1,e2不共线,所以t=1,2t=k,所以k=2,故选A.5.已知非零向量OA,OB不共线,且2OP=xOA+yOB,若PA=λAB(λ∈R),则x,y满足的关系是(A)A.x+y-2=0B.2x+y-1=0C.x+2y-2=0D.2x+y-2=0解析:由PA=λAB,得OA-OP=λ(OB-OA),即OP=(1+λ)·OA-λOB.又2OP=xOA+yOB,∴消去λ得x+y=2.6.已知四边形ABCD是菱形,点P在对角线AC上(不包括端点),则AP=(A)A.λ(AB+AD),λ∈(0,1)B.λ(AB+BC),λ∈(0,)C.λ(AB-AD),λ∈(0,1)D.λ(AB-BC),λ∈(0,)解析:如图所示,AC=AB+AD,又点P在AC上,∴AP与AC同向,且|AP|<|AC|,故AP=λ(AB+AD),λ∈(0,1).二、填空题7.设一直线上三点A,B,P满足AP=λPB(λ≠±1),O为平面内任意一点,则OP用OA,OB表示为OP=.解析:∵OP=OA+λPB=OA+λ(OB-OP)=OA+λOB-λOP,∴(1+λ)OP=OA+λOB,∴OP=.8.已知向量a,b为平面内所有向量的一组基底,且AB=a+2b,BC=-5a+6b,CD=7a-2b,则A,B,C,D四点中一定共线的三点是A,B,D.解析:BD=BC+CD=(-5a+6b)+(7a-2b)=2a+4b=2(a+2b)=2AB,所以A,B,D三点共线.9.在△ABC中,AB=a,BC=b,AD为边BC的中线,G为△ABC的重心,则用a,b表示向量AG=a+b.解析:依题意得,AG=AD=×(AB+AC)=AB+(BC+AB)=AB+BC=a+b.三、解答题10.设M,N,P是△ABC三边上的点,它们使BM=BC,CN=CA,AP=AB,若AB=c,AC=b,试用c,b作基底,将MN,NP,PM表示出来.解:如图,MN=CN-CM=-AC-CB=-AC-(AB-AC)=AC-AB=b-c.NP=AP-AN=AB-AC=c-b.PM=-MP=-(MN+NP)=c-b-c+b=c+b.11.如图,已知M为△ABC的边BC上一点,且满足AM=AB+AC,求△ABM与△ABC的面积之比.解:∵AM=AB+AC,∴AM=(MB-MA)+(MC-MA),∴MB+MC=0,∴MC=3BM,∴==.——能力提升类——12.已知A,B,C是平面上不共线的三点,O是△ABC的重心,动点P满足OP=(OA+OB+2OC),则点P一定为(B)A.AB边中线的中点B.AB边中线的三等分点(非重心)C.△ABC的重心D.AB边的中点解析:∵O是△ABC的重心,∴OA+OB+OC=0,∴OP=(-OC+2OC)=OC,∴点P是线段OC的中点,即AB边中线的三等分点(非重心).故选B.13.已知平行四边形ABCD中,E为CD的中点,AP=yAD,AQ=xAB,其中x,y∈R,且均不为0.若PQ∥BE,则=.解析:∵PQ=AQ-AP=xAB-yAD,由PQ∥BE,可设PQ=λBE,即xAB-yAD=λ(CE-CB)=λ(-AB+AD)=-AB+λAD,∴则=.14.已知非零向量a,b,c满足a+b+c=0,向量a,b的夹角为120°,且|b|=2|a|,则向量b与c的夹角为150°.解析:由题意画出图形如图,因为a,b的夹角为120°,所以∠CAB=60°,又|b|=2|a|,所以∠ACB=90°,所以∠ABC=30°,即b与c的夹角为150°.15.如图所示,D,E,F分别是△ABC的边BC,CA,AB上的点,AD与EF相交于点G,已知CD=2DB,AF=4FB,AG=mAD,AE=tAC.(1)试用AB,AC表示AD;(2)若m=,求t的值.解:(1)因为BD=BC=(AC-AB)=AC-AB,所以AD=AB+BD=AB+=AB+AC.(2)依题意知,AF=AB,AE=tAC,AG=AD=AB+AC,所以FG=AG-AF=AC-AB,FE=AE-AF=tAC-AB.因为E,F,G三点共线,所以FG=λFE,所以=tλ,-=-λ,解得t=.