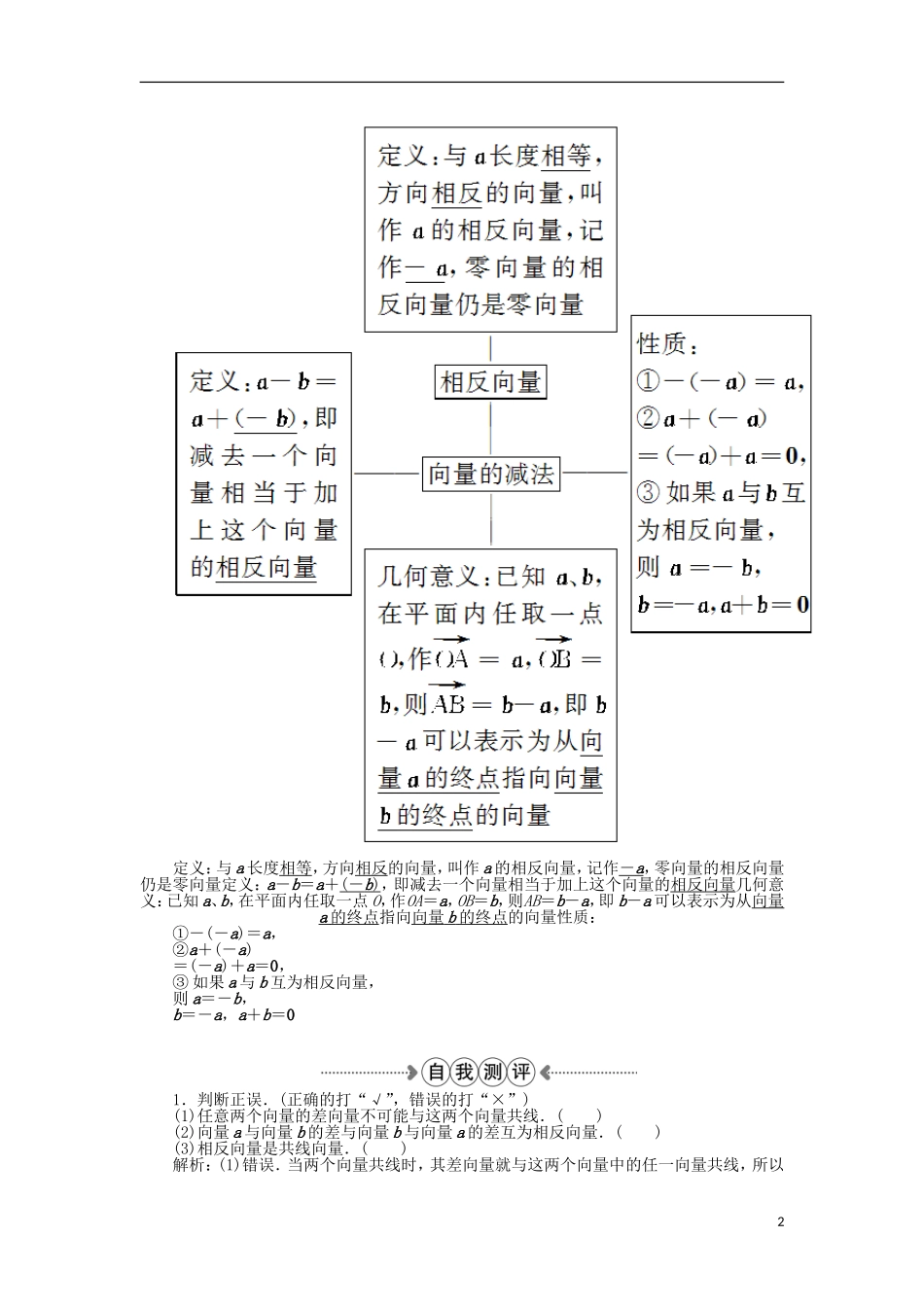
2.2向量的减法1.问题导航(1)两个向量共线时,如何作出其差向量?(2)点O,A,B为平面中的任意三点,则AB=OB-OA对吗?(3)在向量运算中a+b=c+d,是否有a-c=d-b成立?2.例题导读P79例4.通过本例学习,学会作已知向量的和或差.P80例5.通过本例学习,学会利用向量加减法的几何意义求向量的和或差的模.试一试:教材P81习题2-2A组T4你会吗?向量的减法1定义:与a长度相等,方向相反的向量,叫作a的相反向量,记作-a,零向量的相反向量仍是零向量定义:a-b=a+(-b),即减去一个向量相当于加上这个向量的相反向量几何意义:已知a、b,在平面内任取一点O,作OA=a,OB=b,则AB=b-a,即b-a可以表示为从向量a的终点指向向量b的终点的向量性质:①-(-a)=a,②a+(-a)=(-a)+a=0,③如果a与b互为相反向量,则a=-b,b=-a,a+b=01.判断正误.(正确的打“√”,错误的打“×”)(1)任意两个向量的差向量不可能与这两个向量共线.()(2)向量a与向量b的差与向量b与向量a的差互为相反向量.()(3)相反向量是共线向量.()解析:(1)错误.当两个向量共线时,其差向量就与这两个向量中的任一向量共线,所以2该说法错误.(2)正确.因为两个向量的差仍然是一个向量,所以向量a与向量b的差与向量b与向量a的差互为相反向量.(3)正确.根据相反向量的定义知,该说法正确.答案:(1)×(2)√(3)√2.下列等式中,正确的个数是()①a+b=b+a;②a-b=b-a;③0-a=-a;④-(-a)=a;⑤a+(-a)=0.A.1B.2C.3D.4解析:选C.由向量的加法及几何意义,可得:①a+b=b+a,正确;由向量的减法及其几何意义,得a-b=-(b-a),即②错误;0-a=-a,③正确;根据相反向量的定义及性质得-(-a)=a,④正确;而a+(-a)=0≠0,⑤错误.3.OC-OA+CD=________.解析:OC-OA+CD=(OC-OA)+CD=AC+CD=AD.答案:AD4.若a与b反向,且|a|=|b|=1,则|a-b|=________.解析:因为a与b反向,所以|a-b|=|a|+|b|=2.答案:21.相反向量满足的两个条件(1)两个向量的方向相反.(2)两个向量的长度相等.2.相反向量的意义(1)在相反向量的基础上,可以通过向量加法定义向量减法.(2)为向量的“移项”提供依据.利用(-a)+a=0在向量等式的两端加上某个向量的相反向量,实现向量的“移项”.3.对向量减法的三点说明(1)减法的几何意义a-b的几何意义是:当向量a,b的起点相同时,从向量b的终点指向向量a的终点的向量.(2)与向量加法的关系a-b=a+(-b),减去一个向量等于加上这个向量的相反向量.(3)向量减法运算法则把减向量与被减向量的起点重合,则差向量是从减向量的终点指向被减向量的终点.已知向量作差向量如图,已知向量a、b、c不共线,求作向量a+b-c.(链接教材P79例4)[解]法一:如图①,在平面内任取一点O,作OA=a,OB=b,OC=c,连接BC,则CB=b-c.过点A作AD綊BC,连接OD,则AD=b-c,所以OD=OA+AD=a+b-c.法二:如图②,在平面内任取一点O,作OA=a,AB=b,连接OB,则OB=a+b,再作OC=c,连接CB,则CB=a+b-c.法三:如图③,在平面内任取一点O,作OA=a,AB=b,连接OB,则OB=a+b,再作CB=c,连接OC,则OC=a+b-c.3方法归纳求两向量的差向量关键是把两向量平移到首首相接的位置,然后利用向量减法的三角形法则来运算.平移作两向量的差的步骤此步骤可以简记为“作平移,共起点,两尾连,指被减”.1.(1)如图,已知向量a,b,c,求作向量a-b-c.(2)如图所示,O为△ABC内一点,OA=a,OB=b,OC=c,求作向量b+c-a.解:(1)作向量OA=a,OB=b,则向量a-b=BA,再作向量BC=c,则向量CA=a-b-c.(2)以OB,OC为邻边作▱OBDC,连接OD,AD,则OD=OB+OC=b+c,AD=OD-OA=b+c-a.向量的减法运算化简下列各式:(1)(AB+MB)+(-OB-MO);(2)AB-AD-DC;(3)(AB-CD)-(AC-BD).(链接教材P81习题2-2A组T5)[解](1)法一:原式=AB+MB+BO+OM=(AB+BO)+(OM+MB)=AO+OB=AB.法二:原式=AB+MB+BO+OM=AB+(MB+BO)+OM=AB+MO+OM=AB+0=AB.(2)法一:原式=DB-DC=CB.法二:原式=AB-(AD+DC)=AB-AC=CB.(3)法一:原式=AB+DC...