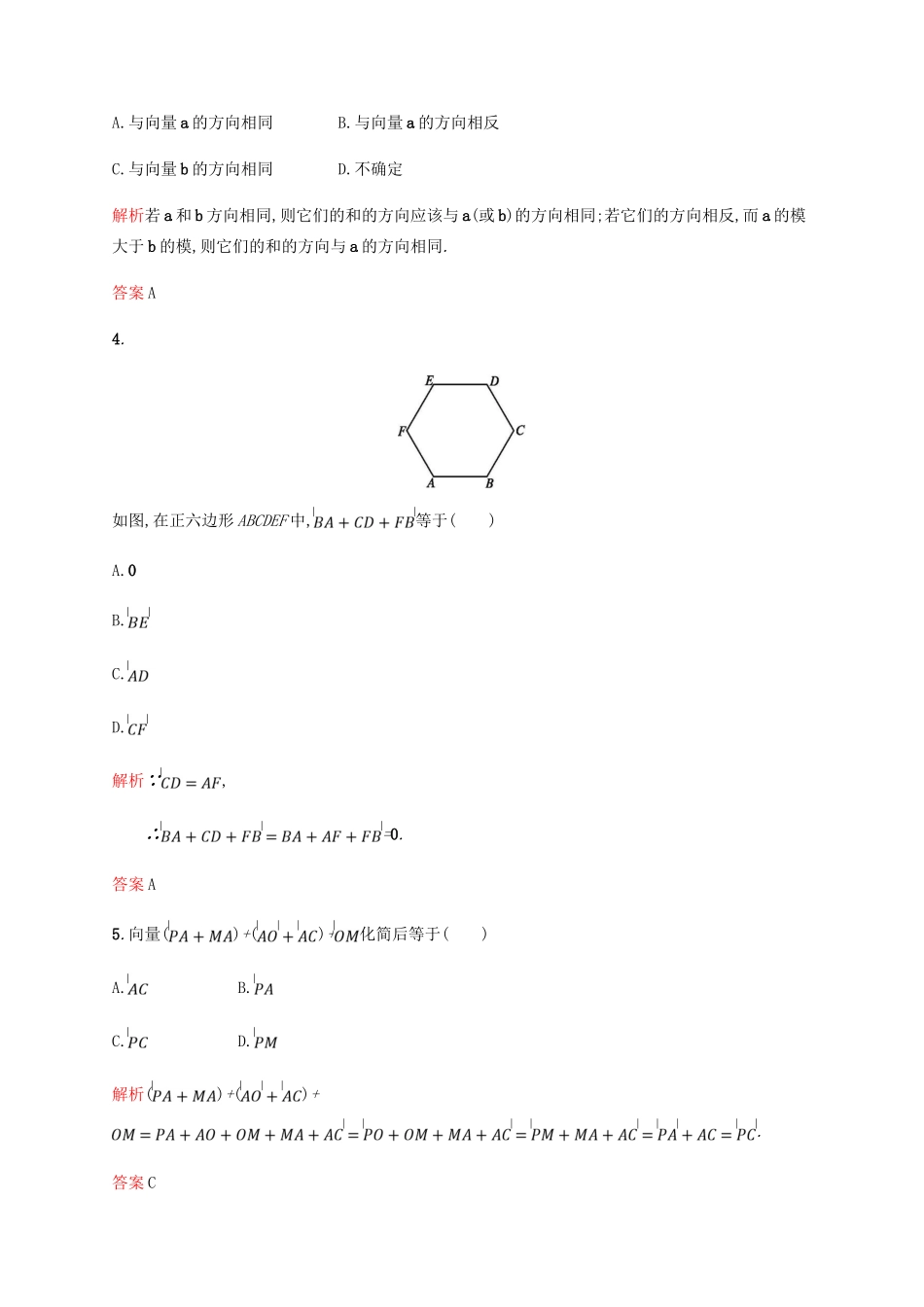
2.2.1向量加法运算及其几何意义课后篇巩固探究A组基础巩固1.在四边形ABCD中,,则四边形ABCD是()A.梯形B.矩形C.正方形D.平行四边形解析由平行四边形法则可得,四边形ABCD是以AB,AD为邻边的平行四边形.答案D2.如图所示,四边形ABCD是梯形,AD∥BC,AC与BD交于点O,则=()A.B.C.D.解析.答案B3.已知向量a∥b,且|a|>|b|>0,则向量a+b的方向()A.与向量a的方向相同B.与向量a的方向相反C.与向量b的方向相同D.不确定解析若a和b方向相同,则它们的和的方向应该与a(或b)的方向相同;若它们的方向相反,而a的模大于b的模,则它们的和的方向与a的方向相同.答案A4.如图,在正六边形ABCDEF中,等于()A.0B.C.D.解析∵,∴=0.答案A5.向量()+()+化简后等于()A.B.C.D.解析()+()+.答案C6.在矩形ABCD中,若AB=2,BC=1,则||=.解析因为ABCD是矩形,所以对角线AC=,于是||=||=.答案7.如图,在平行四边形ABCD中,写出下列各式的结果:(1)=;(2)=;(3)=;(4)=.解析(1)由平行四边形法则可知为;(2);(3);(4)=0.答案(1)(2)(3)(4)08.如图所示,若P为△ABC的外心,且,则∠ACB=.解析因为P为△ABC的外心,所以PA=PB=PC,因为,由向量的线性运算可得四边形PACB是菱形,且∠PAC=60°,所以∠ACB=120°.答案120°9.是否存在a,b,使|a+b|=|a|=|b|?请画出图形说明.解存在,如图,=a,=b,OA=OB=OC,∠AOB=120°,∠AOC=∠COB=60°.10.如图所示,P,Q是△ABC的边BC上两点,且BP=QC.求证:.证明∵,∴.∵大小相等,方向相反,∴=0.故+0=.B组能力提升1.已知四边形ABCD为菱形,则下列等式中成立的是()A.B.C.D.解析因为四边形ABCD是菱形,所以也是平行四边形,于是,故C项正确.答案C2.设a=()+(),b是任一非零向量,则在下列结论中:①a∥b;②a+b=a;③a+b=b;④|a+b|<|a|+|b|;⑤|a+b|=|a|+|b|.正确结论的序号是()A.①⑤B.②④⑤C.③⑤D.①③⑤解析∵a=()+()==0,又b为任一非零向量,∴①③⑤均正确.答案D3.如图,已知电线AO与天花板的夹角为60°,电线AO所受拉力|F1|=24N.绳BO与墙壁垂直,所受拉力|F2|=12N,则F1与F2的合力大小为,方向为.解析以为邻边作平行四边形BOAC,则F1+F2=F,即,则∠OAC=60°,||=24,||=||=12,∴∠ACO=90°,∴||=12.∴F1与F2的合力大小为12N,方向为竖直向上.答案12N竖直向上4.如图,在△ABC中,O为重心,D,E,F分别是BC,AC,AB的中点,化简下列三式:(1);(2);(3).解(1).(2)=()+.(3).5.一艘船在水中航行,水流速度与船在静水中航行的速度均为5km/h.如果此船实际向南偏西30°方向行驶2km,然后又向西行驶2km,你知道此船在整个过程中的位移吗?解如图,用表示船的第一次位移,用表示船的第二次位移,根据向量加法的三角形法则知,所以可表示两次位移的和位移.由题意知,在Rt△ABC中,∠BAC=30°,则BC=AC=1,AB=.在等腰三角形ACD中,AC=CD=2,所以∠D=∠DAC=∠ACB=30°,所以∠BAD=60°,AD=2AB=2,所以两次位移的和位移的方向是南偏西60°,位移的大小为2km.6.如图所示,一架飞机从A地按北偏东35°的方向飞行800km到达B地,然后又从B地按南偏东55°的方向飞行600km到达C地,求这架飞机飞行的路程及两次位移的和(参考数据:sin37°=0.6).解设分别表示飞机从A地按北偏东35°的方向飞行800km,从B地按南偏东55°的方向飞行600km,则飞机飞行的路程指的是||+||;两次位移的和指的是.依题意,有||+||=800+600=1400(km),∠ABC=35°+55°=90°.在Rt△ABC中,||==1000(km),其中∠BAC=37°,所以方向为北偏东35°+37°=72°.从而飞机飞行的路程是1400km,两次飞行的位移和的大小为1000km,方向为北偏东72°.