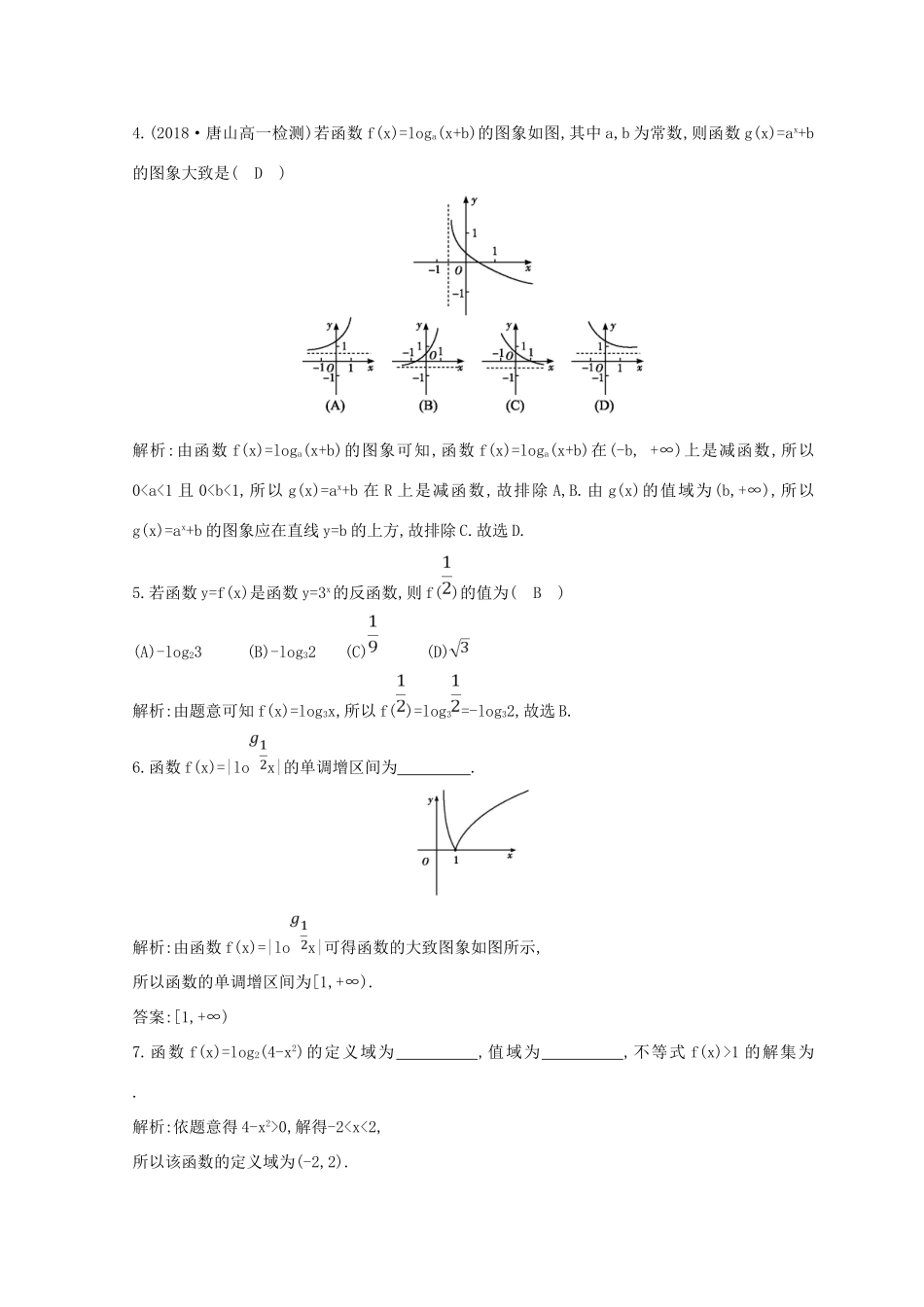
第一课时对数函数的图象及性质【选题明细表】知识点、方法题号对数函数的定义及性质1,2,10,11,12,13对数函数的图象特征4,6,9与对数函数有关的定义域问题3,7,8反函数51.对数函数的图象过点M(16,4),则此对数函数的解析式为(D)(A)y=log4x(B)y=lox(C)y=lox(D)y=log2x解析:设对数函数为y=logax(a>0,且a≠1),由于对数函数的图象过点M(16,4),所以4=loga16,得a=2.所以对数函数的解析式为y=log2x,故选D.2.下列函数①y=2x;②y=log0.5(x+1);③y=;④y=|x-1|中,在区间(0,1)上单调递减的函数的序号是(D)(A)①③(B)②③(C)①④(D)②④解析:函数①y=2x在区间(0,1)上单调递增;②y=log0.5(x+1)在区间(0,1)上单调递减;③y=在区间(0,1)上单调递增;④y=|x-1|在区间(0,1)上单调递减.故选D.3.(2018·长沙高一月考)函数f(x)=+lg(1+x)的定义域是(C)(A)(-∞,-1)(B)(1,+∞)(C)(-1,1)∪(1,+∞)(D)(-∞,+∞)解析:由题意知解得x>-1,且x≠1.故选C.4.(2018·唐山高一检测)若函数f(x)=loga(x+b)的图象如图,其中a,b为常数,则函数g(x)=ax+b的图象大致是(D)解析:由函数f(x)=loga(x+b)的图象可知,函数f(x)=loga(x+b)在(-b,+∞)上是减函数,所以0
1的解集为.解析:依题意得4-x2>0,解得-20,所以(4-x2)max=4,所以在(-2,2)上,该函数的值域为(-∞,2].由f(x)>1得到log2(4-x2)>1,则4-x2>2,解得-1的解集为(-,).答案:(-2,2)(-∞,2](-,)8.已知函数f(x)=loga(1+x),g(x)=loga(1-x)(a>0且a≠1).(1)设a=2,函数f(x)的定义域为[3,63],求函数f(x)的最值;(2)求使f(x)-g(x)>0的x的取值范围.解:(1)当a=2时,函数f(x)=log2(x+1)为[3,63]上的增函数,故f(x)max=f(63)=log2(63+1)=6,f(x)min=f(3)=log2(3+1)=2.(2)f(x)-g(x)>0,即loga(1+x)>loga(1-x).①当a>1时,1+x>1-x>0,得01时,x∈(0,1),00的x的取值范围是.解析:根据题意画出f(x)的草图,由图象可知,f(x)>0的x的取值范围是-11.答案:(-1,0)∪(1,+∞)11.函数f(x)=log2(-1)(x>8)的值域是.解析:因为x>8,所以-1>2,由于对数函数的底数2大于1,说明函数为增函数.所以f(x)>log22=1,故函数的值域为(1,+∞).答案:(1,+∞)12.设f(x)=(1)求f(log2)的值;(2)求f(x)的最小值.解:(1)因为log20,所以2x=1+,x=log2(1+).(2)当t∈[1,2]时,2t(22t-)+m(2t-)≥0,即m(22t-1)≥-(24t-1).因为22t-1>0,所以m≥-(22t+1).因为t∈[1,2],所以-(1+22t)∈[-17,-5].故m的取值范围是[-5,+∞).