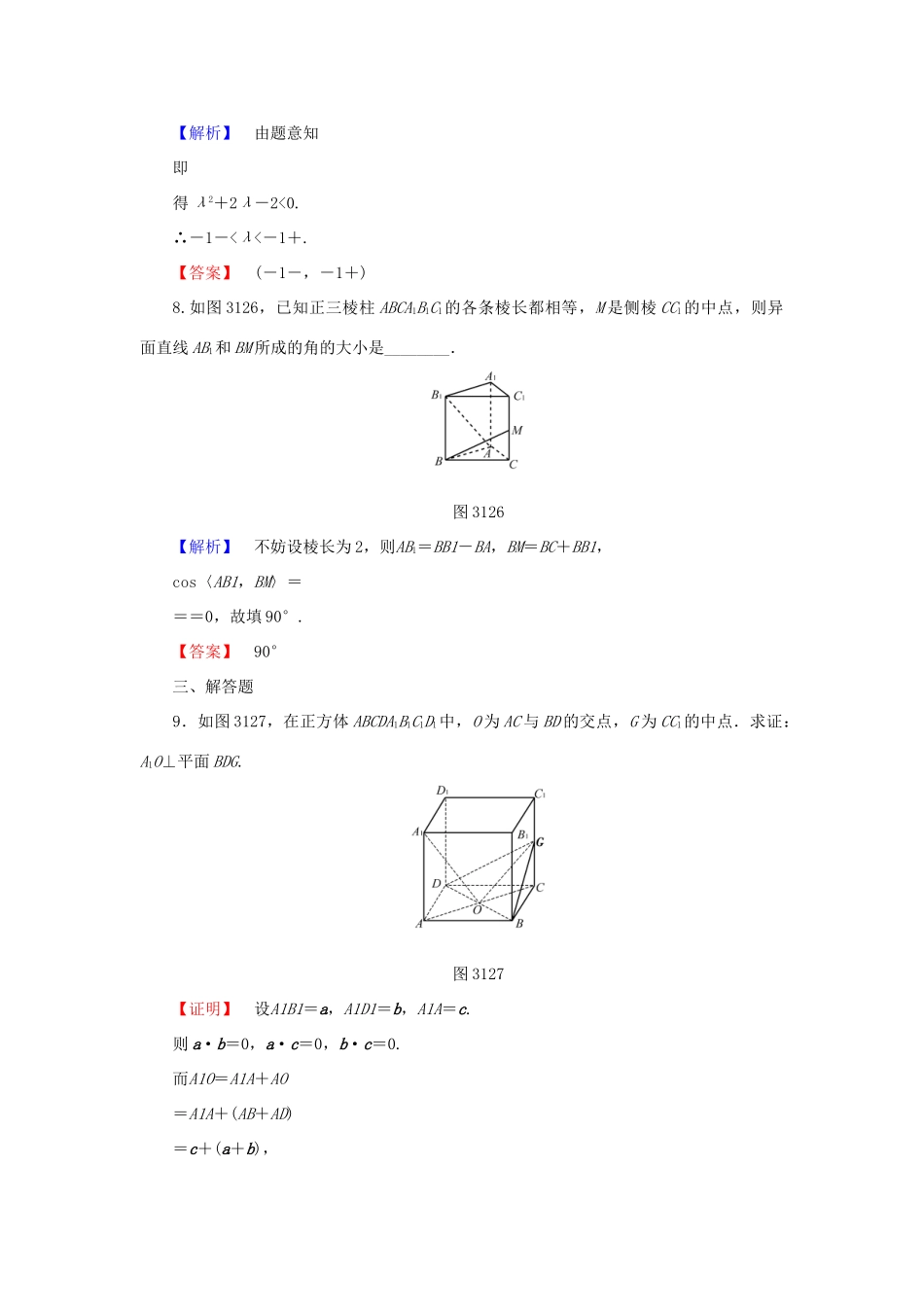
【课堂新坐标】2016-2017学年高中数学第三章空间向量与立体几何3.1.3空间向量的数量积运算学业分层测评新人教A版选修2-1(建议用时:45分钟)[学业达标]一、选择题1.设a,b,c是任意的非零平面向量,且它们相互不共线,下列命题:①(a·b)c-(c·a)b=0;②|a|=;③a2b=b2a;④(3a+2b)·(3a-2b)=9|a|2-4|b|2.其中正确的有()A.①②B.②③C.③④D.②④【解析】由于数量积不满足结合律,故①不正确,由数量积的性质知②正确,③中,|a|2·b=|b|2·a不一定成立,④运算正确.【答案】D2.已知a+b+c=,|a|=2,|b|=3,|c|=4,则a与b的夹角〈a,b〉=()A.30°B.45°C.60°D.以上都不对【解析】 a+b+c=0,∴a+b=-c,∴(a+b)2=|a|2+|b|2+2a·b=|c|2,∴a·b=,∴cos〈a,b〉==.【答案】D3.已知四边形ABCD为矩形,PA⊥平面ABCD,连接AC,BD,PB,PC,PD,则下列各组向量中,数量积不为零的是()A.PC与BDB.DA与PBC.PD与ABD.PA与CD【解析】用排除法,因为PA⊥平面ABCD,所以PA⊥CD,故PA·CD=0,排除D;因为AD⊥AB,PA⊥AD,又PA∩AB=A,所以AD⊥平面PAB,所以AD⊥PB,故DA·PB=0,排除B,同理PD·AB=0,排除C.【答案】A4.如图3125,已知空间四边形每条边和对角线都等于a,点E,F,G分别是AB,AD,DC的中点,则下列向量的数量积等于a2的是()图3125A.2BA·ACB.2AD·DBC.2FG·ACD.2EF·CB【解析】2BA·AC=-a2,故A错;2AD·DB=-a2,故B错;2EF·CB=-a2,故D错;2FG·AC=AC2=a2,故只有C正确.【答案】C5.在正方体ABCDA1B1C1D1中,有下列命题:①(AA1+AD+AB)2=3AB2;②A1C·(A1B1-A1A)=0;③AD1与A1B的夹角为60°.其中正确命题的个数是()【导学号:18490091】A.1个B.2个C.3个D.0个【解析】由题意知①②都正确,③不正确,AD1与A1B的夹角为120°.【答案】B二、填空题6.已知|a|=2,|b|=3,〈a,b〉=60°,则|2a-3b|=________.【解析】|2a-3b|2=(2a-3b)2=4a2-12a·b+9b2=4×|a|2+9×|b|2-12×|a|·|b|·cos60°=61,∴|2a-3b|=.【答案】7.已知|a|=2,|b|=1,〈a,b〉=60°,则使向量a+λb与λa-2b的夹角为钝角的实数λ的取值范围是________.【解析】由题意知即得λ2+2λ-2<0.∴-1-<λ<-1+.【答案】(-1-,-1+)8.如图3126,已知正三棱柱ABCA1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是________.图3126【解析】不妨设棱长为2,则AB1=BB1-BA,BM=BC+BB1,cos〈AB1,BM〉===0,故填90°.【答案】90°三、解答题9.如图3127,在正方体ABCDA1B1C1D1中,O为AC与BD的交点,G为CC1的中点.求证:A1O⊥平面BDG.图3127【证明】设A1B1=a,A1D1=b,A1A=c.则a·b=0,a·c=0,b·c=0.而A1O=A1A+AO=A1A+(AB+AD)=c+(a+b),BD=AD-AB=b-a,OG=OC+CG=(AB+AD)+CC1=(a+b)+c.∴A1O·BD=·(b-a)=c·(b-a)+(a+b)·(b-a)=c·b-c·a+(b2-a2)=(|b|2-|a|2)=0.∴A1O⊥BD.∴A1O⊥BD.同理可证A1O⊥OG.∴A1O⊥OG.又OG∩BD=O且A1O⊄平面BDG,∴A1O⊥平面BDG.10.已知长方体ABCDA1B1C1D1中,AB=AA1=2,AD=4,E为侧面AB1的中心,F为A1D1的中点,试计算:(1)BC·ED1;(2)BF·AB1;(3)EF·FC1.【解】如图所示,设AB=a,AD=b,AA1=c,则|a|=|c|=2,|b|=4,a·b=b·c=c·a=0.(1)BC·ED1=AD·(EA1+A1D1)=AD·=b·=|b|2=42=16.(2)BF·AB1=(BA1+A1F)·(AB+BB1)=·(AB+AA1)=·(a+c)=|c|2-|a|2=22-22=0.(3)EF·FC1=(EA1+A1F)·(FD1+D1C1)=·=·=(-a+b+c)·=-|a|2+|b|2=2.[能力提升]1.已知边长为1的正方体ABCDA1B1C1D1的上底面A1B1C1D1的中心为O1,则AO1·AC的值为()A.-1B.0C.1D.2【解析】AO1=AA1+A1O1=AA1+(A1B1+A1D1)=AA1+(AB+AD),而AC=AB+AD,则AO1·AC=(AB2+AD2)=1,故选C.【答案】C2.已知a,b是两异面直线,A,B∈a,C,D∈b,AC⊥b,BD⊥b且AB=2,CD=1,则直线a,b所成的角为()A.30°B.60°C.90°D.45°【解析】由于AB=AC+CD+DB,则AB·CD=(AC+CD+DB)·CD=CD2=1.cos〈...