高中数学 第三章 基本初等函数（Ⅰ）3.2 对数与对数函数 3.2.2 对数函数同步训练 新人教B版必修1-新人教B版高一必修1数学试题VIP免费

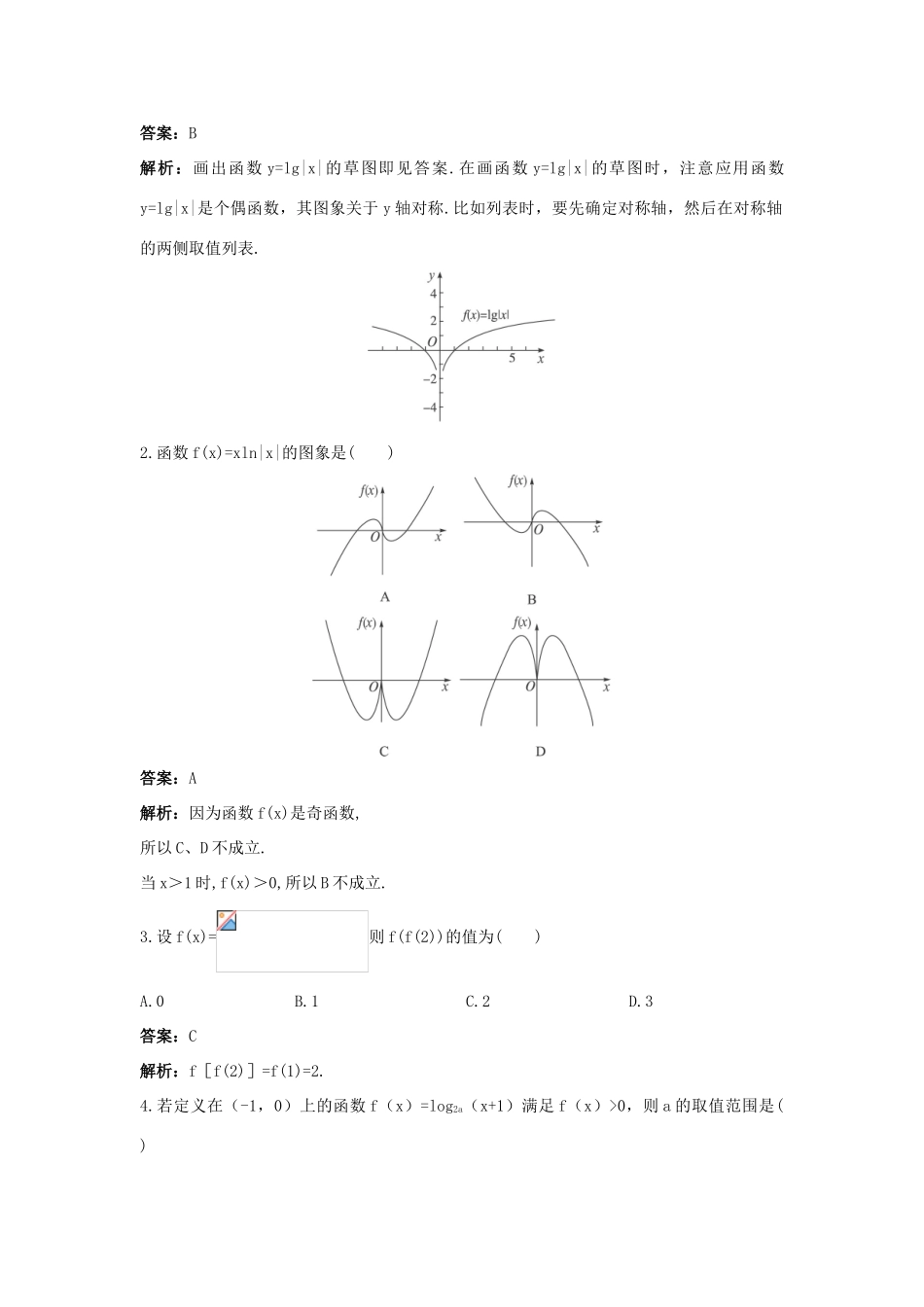
3.2.2对数函数5分钟训练1.函数y=的定义域是()A.(3,+∞)B.［3,+∞)C.(4,+∞)D.［4,+∞)答案：D解析：由log2x-2≥0,得x≥4.2.函数f(x)=|log2x|的图象是()答案：A解析：f(x)=3.设a=0.3-2,b=log0.34,c=log43,则a、b、c的大小关系是()A.a＜b＜cB.a＜c＜bC.c＜b＜aD.b＜c＜a答案：D解析：利用它们与0、1的大小关系进行比较.4.函数f（x）=log（a-1）x是减函数，则a的取值范围是______________.答案：1＜a＜2解析：由题意知0＜a-1＜1，∴1＜a＜2.10分钟训练1.函数y=lg|x|是()A.偶函数，在区间（-∞，0）上单调递增B.偶函数，在区间（-∞，0）上单调递减C.奇函数，在区间（0，+∞）上单调递增D.奇函数，在区间（0，+∞）上单调递减答案：B解析：画出函数y=lg|x|的草图即见答案.在画函数y=lg|x|的草图时，注意应用函数y=lg|x|是个偶函数，其图象关于y轴对称.比如列表时，要先确定对称轴，然后在对称轴的两侧取值列表.2.函数f(x)=xln|x|的图象是()答案：A解析：因为函数f(x)是奇函数,所以C、D不成立.当x＞1时,f(x)＞0,所以B不成立.3.设f(x)=则f(f(2))的值为()A.0B.1C.2D.3答案：C解析：f［f(2)］=f(1)=2.4.若定义在（-1，0）上的函数f（x）=log2a（x+1）满足f（x）>0，则a的取值范围是()A.（0，）B.（0，］C.（，+∞）D.（0，+∞）答案：A解析：当x∈(-1，0)时，有x+1∈(0，1)，此时要满足f(x)>0，只要0<2a<1即可.由此解得0n>1.5.已知函数y=lg(2x-b)(b为常数),若x∈［1,+∞)时,f(x)≥0恒成立,则()A.b≤1B.b＜1C.b≥1D.b=1答案：A解析：由题意得,2x-b≥1,b≤2x-1,x∈［1,+∞).此时(2x-1)min=1,从而b≤1.6.(创新题)设函数f(x)=logax(a＞0,且a≠1),若f(x1·x2·…·x2007)=8,则f(x12)+f(x22)+…+f(x20072)的值等于()A.4B.8C.16D.2loga8答案：C解析：∵f(x)=logax,f(x1·x2·…·x2007)=8,∴由函数的运算性质,得f(x12)+f(x22)+…+f(x20072)=f(x12·x22·…·x20072)=f［(x1·x2·…·x2007)2］=loga(x1·x2·…·x2007)2=2loga(x1·x2·…·x2007)=2×8=16.7.若f(x)=则满足f(x)=的x的值为_______________.答案：1或3解析：当时,x=1;当log81x=时,x==3.所以x的值为1或3.8.(探究题)对于函数f(x)定义域中任意的x1,x2(x1≠x2),有如下结论：①f(x1+x2)=f(x1)·f(x2);②f(x1·x2)=f(x1)+f(x2);③＞0;④f()＜［f(x1)+f(x2)］.当f(x)=lgx时,上述结论成立的是_________________.(填序号)答案：②③提示:根据对数的运算性质及函数的性质进行判断.9.已知集合A={x|＜1},B={x|log4(x+a)＜1},若A∩B=,求实数a的取值范围.解：由＜1,得x2-x-6＞0,解得x＜-2或x＞3,即A={x|x＜-2或x＞3}.由log4(x+a)＜1,得0＜x+a＜4,解得-a＜x＜4-a,即B={x|-a＜x＜4-a}.∵A∩B=,∴解得1≤a≤2.即实数a的取值范围是［1,2］.10.已知函数f(x)=loga(a＞0,且a≠1)的图象关于原点对称.(1)求m的值;(2)判断f(x)在(1,+∞)上的单调性,并根据定义证明.解：(1)根据已知条件对于定义域内的一切x都有f(-x)=-f(x),即f(-x)+f(x)=0,∴=0.整理得=0,∴=1,即(m2-1)x2=0.∴m2-1=0.∴m=1或m=-1.若m=1,=-1,f(x)无意义,则舍去m=1,∴m=-1.(2)设1＜x1＜x2,而f(x)=loga,∵,∴＞0.当a＞1时,,即f(x)在(1,+∞)上递减；当0＜a＜1时,,即f(x)在(1,+∞)上递增.