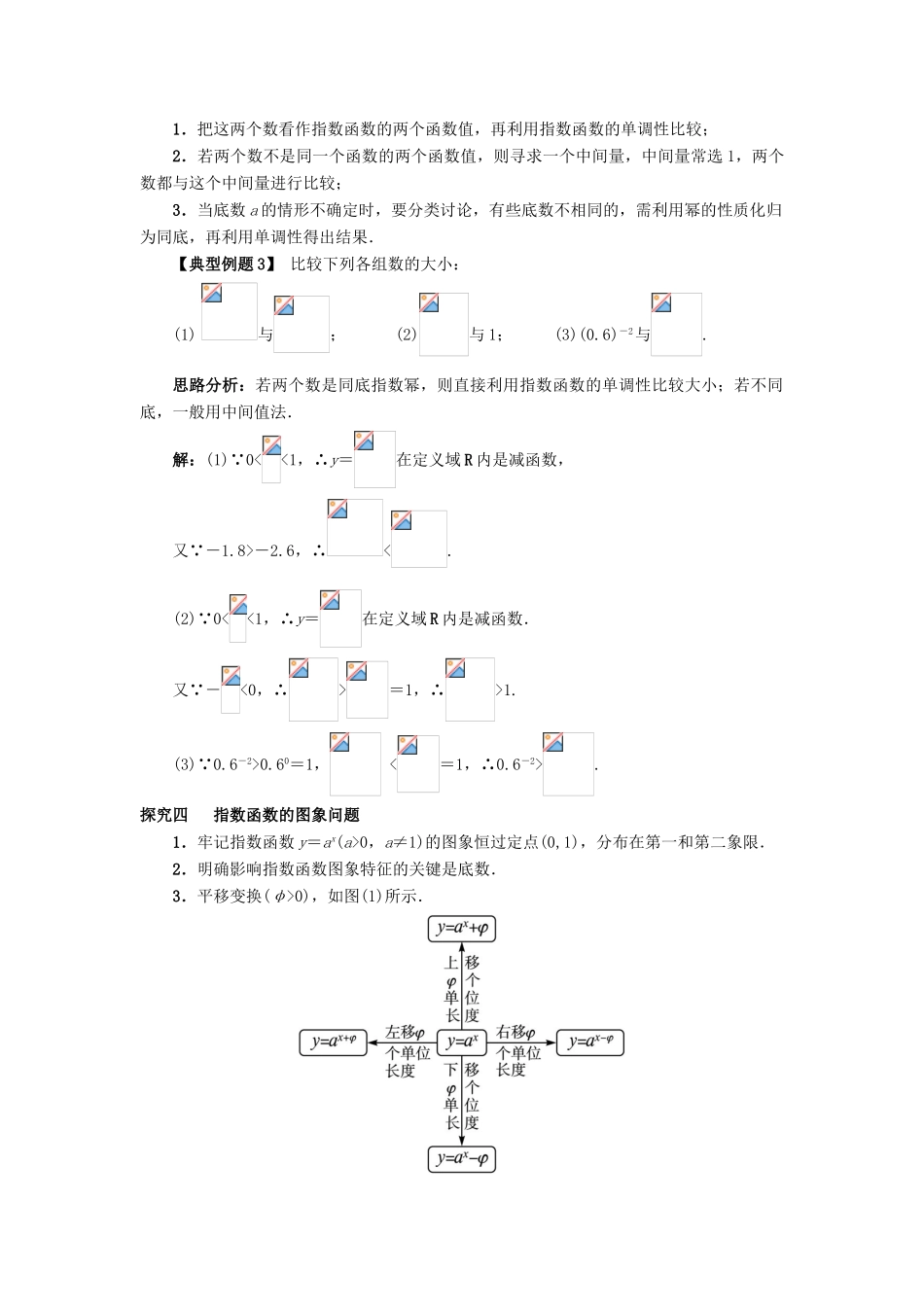
3.1.2指数函数课堂探究探究一指数函数的概念1.判断一个函数是指数函数的方法:(1)看形式:即看是否符合y=ax(a>0,a≠1,x∈R)这一结构形式.(2)明特征:指数函数的解析式具备的三个特征,只要有一个特征不具备,则不是指数函数.2.已知某个函数是指数函数求参数值的步骤(1)列:依据指数函数解析式所具备的三个特征,列出方程(组)或不等式(组).(2)解:解所列的方程(组)或不等式(组),求出参数的值或范围.【典型例题1】函数y=(a2-3a+3)ax是指数函数,求a的值.思路分析:只需让解析式符合y=ax这一形式即可.解:因为y=(a2-3a+3)ax是指数函数,所以解得所以a=2.探究二求指数型函数的定义域、值域求函数的定义域问题,即求表达式有意义时相应的x的取值范围(集合);求函数的值域问题主要是借助指数函数的性质,先求出指数位置上的表达式的取值范围,再求原函数的值域.【典型例题2】求下列函数的定义域与值域:(1)y=;(2)y=;(3)y=.解:(1)要使函数y=2有意义,则有x-3≠0,即x≠3;因为≠0,所以y=≠1.所以所求函数的定义域是{x|x∈R,且x≠3},值域为{y|y>0,且y≠1}.(2)因为y=中的|x|≥0,所以0<y≤1.所以所求函数的定义域为R,值域为{y|0<y≤1}.(3)已知函数可化为y=,由≥0,得x>1.又由>0,得y=>1.所以所求函数的定义域为{x|x>1},值域为{y|y>1}.探究三利用指数函数的性质比较大小利用指数函数的性质比较大小的方法:1.把这两个数看作指数函数的两个函数值,再利用指数函数的单调性比较;2.若两个数不是同一个函数的两个函数值,则寻求一个中间量,中间量常选1,两个数都与这个中间量进行比较;3.当底数a的情形不确定时,要分类讨论,有些底数不相同的,需利用幂的性质化归为同底,再利用单调性得出结果.【典型例题3】比较下列各组数的大小:(1)与;(2)与1;(3)(0.6)-2与.思路分析:若两个数是同底指数幂,则直接利用指数函数的单调性比较大小;若不同底,一般用中间值法.解:(1) 0<<1,∴y=在定义域R内是减函数,又 -1.8>-2.6,∴<.(2) 0<<1,∴y=在定义域R内是减函数.又 -<0,∴>=1,∴>1.(3) 0.6-2>0.60=1,<=1,∴0.6-2>.探究四指数函数的图象问题1.牢记指数函数y=ax(a>0,a≠1)的图象恒过定点(0,1),分布在第一和第二象限.2.明确影响指数函数图象特征的关键是底数.3.平移变换(φ>0),如图(1)所示.图(1)图(2)4.对称变换,如图(2)所示.【典型例题4】函数y=ax-1+2(a>0,且a≠1)的图象恒过定点__________.解析:方法一: 指数函数y=ax(a>0,a≠1)的图象过定点(0,1),∴函数y=ax-1+2中令x-1=0,即x=1,则y=1+2=3.∴函数图象恒过定点(1,3).方法二:函数可变形为y-2=ax-1,把y-2看作x-1的指数函数,则当x-1=0,即x=1时,y-2=1,即y=3.∴函数图象恒过定点(1,3).方法三:由图象变换可知: 指数函数y=ax(a>0,且a≠1)的图象过定点(0,1),∴y=ax-1的图象恒过定点(1,1).∴y=ax-1+2的图象恒过点(1,3).答案:(1,3)【典型例题5】先作出函数y=2x的图象,再通过图象变换作出下列函数的图象:(1)y=2x-2,y=2x+1;(2)y=2x+1,y=2x-2;(3)y=-2x,y=2-x,y=-2-x.思路分析:先作出y=2x的图象,再向左(右)、上(下)平移分别得到第(1)(2)题中函数的图象;由y=2x的图象作关于x轴、y轴、原点的对称变换便得第(3)题中函数的图象.解:列表:x…-3-2-10123…y=2x…1248…根据上表中x,y的对应值在平面直角坐标系中描点作图如图(1)所示.图(1)(1)函数y=2x-2的图象可以由y=2x的图象向右平移2个单位长度得到,函数y=2x+1的图象可以由y=2x的图象向左平移1个单位长度得到.图象如图(1)所示.(2)函数y=2x+1的图象可以由y=2x的图象向上平移1个单位长度得到,函数y=2x-2的图象可以由y=2x的图象向下平移2个单位长度得到.图象如图(2)所示.图(2)(3)函数y=2-x的图象由y=2x的图象关于y轴对称后得到;函数y=-2x的图象由y=2x的图象关于x轴对称后得到;函数y=-2-x的图象由y=2x的图象关于原点对称后得到.图象如图(3)所示.图(3)探究五易错辨析易错点误解“左加右减”法...