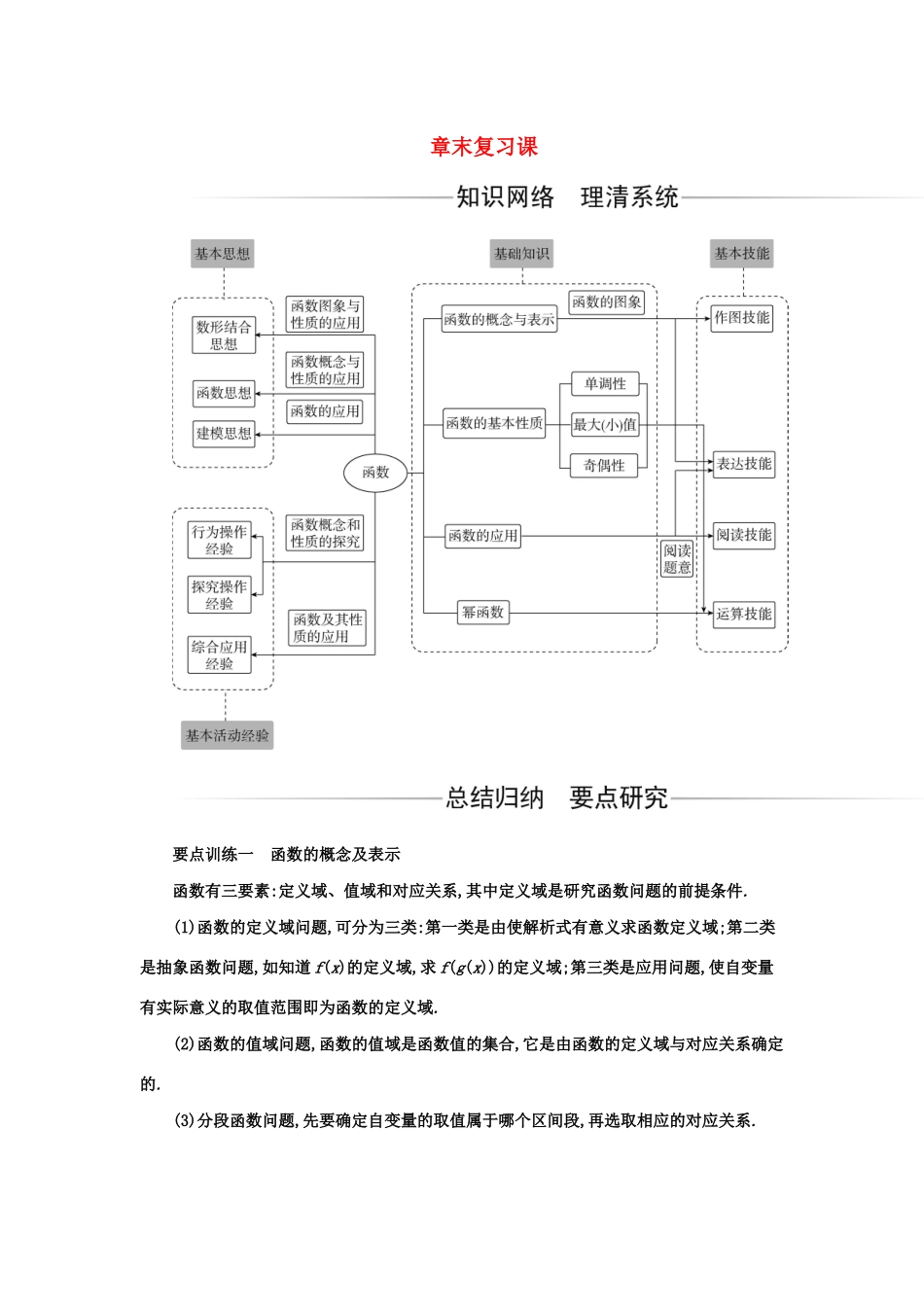
章末复习课要点训练一函数的概念及表示函数有三要素:定义域、值域和对应关系,其中定义域是研究函数问题的前提条件.(1)函数的定义域问题,可分为三类:第一类是由使解析式有意义求函数定义域;第二类是抽象函数问题,如知道f(x)的定义域,求f(g(x))的定义域;第三类是应用问题,使自变量有实际意义的取值范围即为函数的定义域.(2)函数的值域问题,函数的值域是函数值的集合,它是由函数的定义域与对应关系确定的.(3)分段函数问题,先要确定自变量的取值属于哪个区间段,再选取相应的对应关系.1.若函数y=f(x)的值域是[12,3],则函数F(x)=f(x)+1f(x)的值域是()A.[12,3]B.[2,103]C.[52,103]D.[3,103]解析:令t=f(x),则12≤t≤3,由函数g(t)=t+1t在区间[12,1]上是减函数,在区间[1,3]上是增函数,且G(12)=52,g(1)=2,g(3)=103,可得值域为[2,103].答案:B2.(山东高考)设f(x)={❑√x,00,00,所以f(x1)-f(x2)>0,即f(x1)>f(x2).所以f(x)=2x+12x在区间(0,12)上单调递减.要点训练三数形结合思想函数的图象是函数的重要表示方法,广泛应用于解题过程中,它具有明显的直观性,通过函数的图象能够把函数重要的性质体现出来,由此可通过数形结合解决问题.数形结合思想,其实质是将抽象的数学语言与直观的图形结合起来,使抽象的思维和形象思维相结合,把问题灵活转化、化难为易、化抽象为具体、化数为形.1.(全国卷Ⅲ)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是()A.月接待游客量逐月增加B.年接待游客量逐...