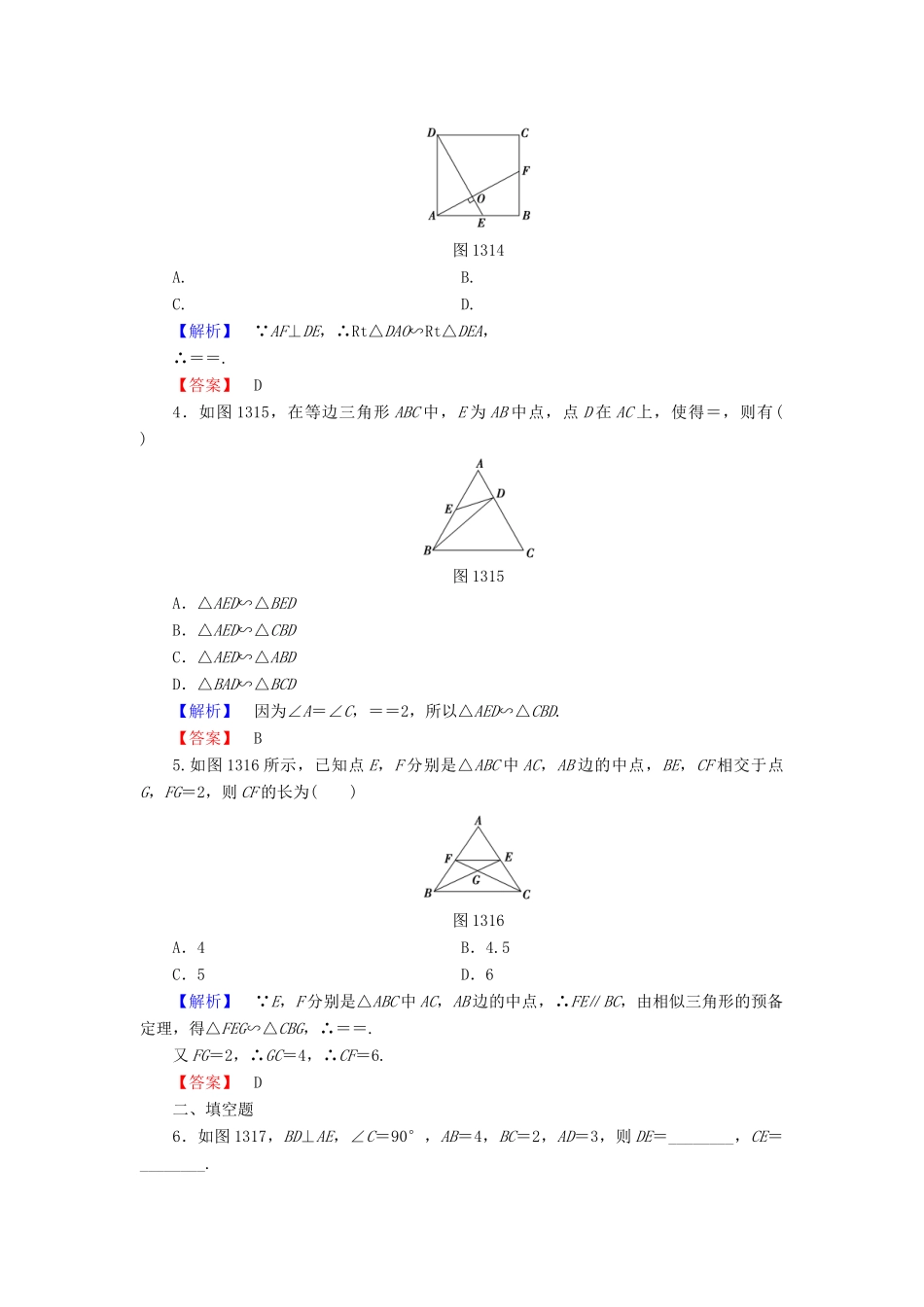
【课堂新坐标】2016-2017学年高中数学第一讲相似三角形的判定及有关性质学业分层测评3相似三角形的判定新人教A版选修4-1(建议用时:45分钟)[学业达标]一、选择题1.如图1312,在正方形网格上有6个三角形:①△ABC,②△BCD,③△BDE,④△BFG,⑤△FGH,⑥△EFK.其中,②~⑥中与三角形①相似的是()图1312A.②③④B.③④⑤C.④⑤⑥D.②③⑥【解析】由相似三角形判定定理知选B.【答案】B2.如图1313,在△ABC中,M在BC上,N在AM上,CM=CN,且=,下列结论中正确的是()图1313A.△ABM∽△ACBB.△ANC∽△AMBC.△ANC∽△ACMD.△CMN∽△BCA【解析】 CM=CN,∴∠CMN=∠CNM. ∠AMB=∠CNM+∠MCN,∠ANC=∠CMN+∠MCN,∴∠AMB=∠ANC.又=,∴△ANC∽△AMB.【答案】B3.如图1314,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则等于()【导学号:07370013】图1314A.B.C.D.【解析】 AF⊥DE,∴Rt△DAO∽Rt△DEA,∴==.【答案】D4.如图1315,在等边三角形ABC中,E为AB中点,点D在AC上,使得=,则有()图1315A.△AED∽△BEDB.△AED∽△CBDC.△AED∽△ABDD.△BAD∽△BCD【解析】因为∠A=∠C,==2,所以△AED∽△CBD.【答案】B5.如图1316所示,已知点E,F分别是△ABC中AC,AB边的中点,BE,CF相交于点G,FG=2,则CF的长为()图1316A.4B.4.5C.5D.6【解析】 E,F分别是△ABC中AC,AB边的中点,∴FE∥BC,由相似三角形的预备定理,得△FEG∽△CBG,∴==.又FG=2,∴GC=4,∴CF=6.【答案】D二、填空题6.如图1317,BD⊥AE,∠C=90°,AB=4,BC=2,AD=3,则DE=________,CE=________.图1317【解析】在Rt△ACE和Rt△ADB中,∠A为公共角,∴△ACE∽△ADB,∴=,∴AE====8,则DE=AE-AD=5,在Rt△ACE中,CE===2.【答案】527.如图1318,∠B=∠D,AE⊥BC,∠ACD=90°,且AB=6,AC=4,AD=12,则AE=________.图1318【解析】由∠B=∠D,AE⊥BC及∠ACD=90°可以推得:Rt△ABE∽Rt△ADC,故=∴AE==2.【答案】28.如图1319,在平行四边形ABCD中,E在DC上,若DE∶EC=1∶2,则BF∶BE=________.【导学号:07370014】图1319【解析】 DE∶EC=1∶2,∴DC∶EC=3∶2,∴AB∶EC=3∶2. AB∥EC,∴△ABF∽△CEF,∴==,∴=.【答案】3∶5三、解答题9.如图1320,已知△ABC中,AB=AC,AD是中线,P是AD上一点,过C作CF∥AB,延长BP交AC于E,交CF于点F.求证:PB2=PE·PF.图1320【证明】连接PC. AB=AC,∴∠ABC=∠ACB. AD是中线,∴AD垂直平分BC,∴PB=PC,∴∠PBD=∠PCD,∴∠ABP=∠ACP.又 CF∥AB,∴∠ABP=∠F=∠ACP,而∠CPE=∠FPC.∴△PCE∽△PFC,∴=,∴PC2=PE·PF,即PB2=PE·PF.10.如图1321,某市经济开发区建有B,C,D三个食品加工厂,这三个工厂和开发区A处的自来水厂正好在一个矩形的四个顶点上,它们之间有公路相通,且AB=CD=900米,AD=BC=1700米.自来水公司已经修好一条自来水主管道AN,B,C两厂之间的公路与自来水主管道交于E处,EC=500米.若自来水主管道到各工厂的自来水管道由各厂负责修建,每米造价800元.图1321(1)要使修建自来水管道的造价最低,这三个工厂的自来水管道路线应怎样设计?并在图中画出该路线;(2)求出各厂所修建的自来水管道的最低造价各是多少元?【解】(1)如图,过B,C,D分别作AN的垂线段BH,CF,DG交AN于H,F,G,BH,CF,DG即为所求的造价最低的管道路线.(2)在Rt△ABE中,AB=900米,BE=1700-500=1200米,∴AE==1500(米),由△ABE∽△CFE,得到=,即=,可得CF=300(米).由△BHE∽△CFE,得=,即=,可得BH=720(米).由△ABE∽△DGA,得=,即=,可得DG=1020(米).所以,B,C,D三厂所建自来水管道的最低造价分别是720×800=576000(元),300×800=240000(元),1020×800=816000(元).[能力提升]1.如图1322所示,要使△ACD∽△BCA,下列各式中必须成立的是()图1322A.=B.=C.AC2=CD·CBD.CD2=AC·AB【解析】∠C=∠C,只有=,即AC2=CD·CB时,才能使△ACD∽△BCA.【答案】C2.如图1323所示,∠AOD=90°,OA=OB=BC=CD,则下列结论正确的是()图1323A.△DAB∽△OCAB...