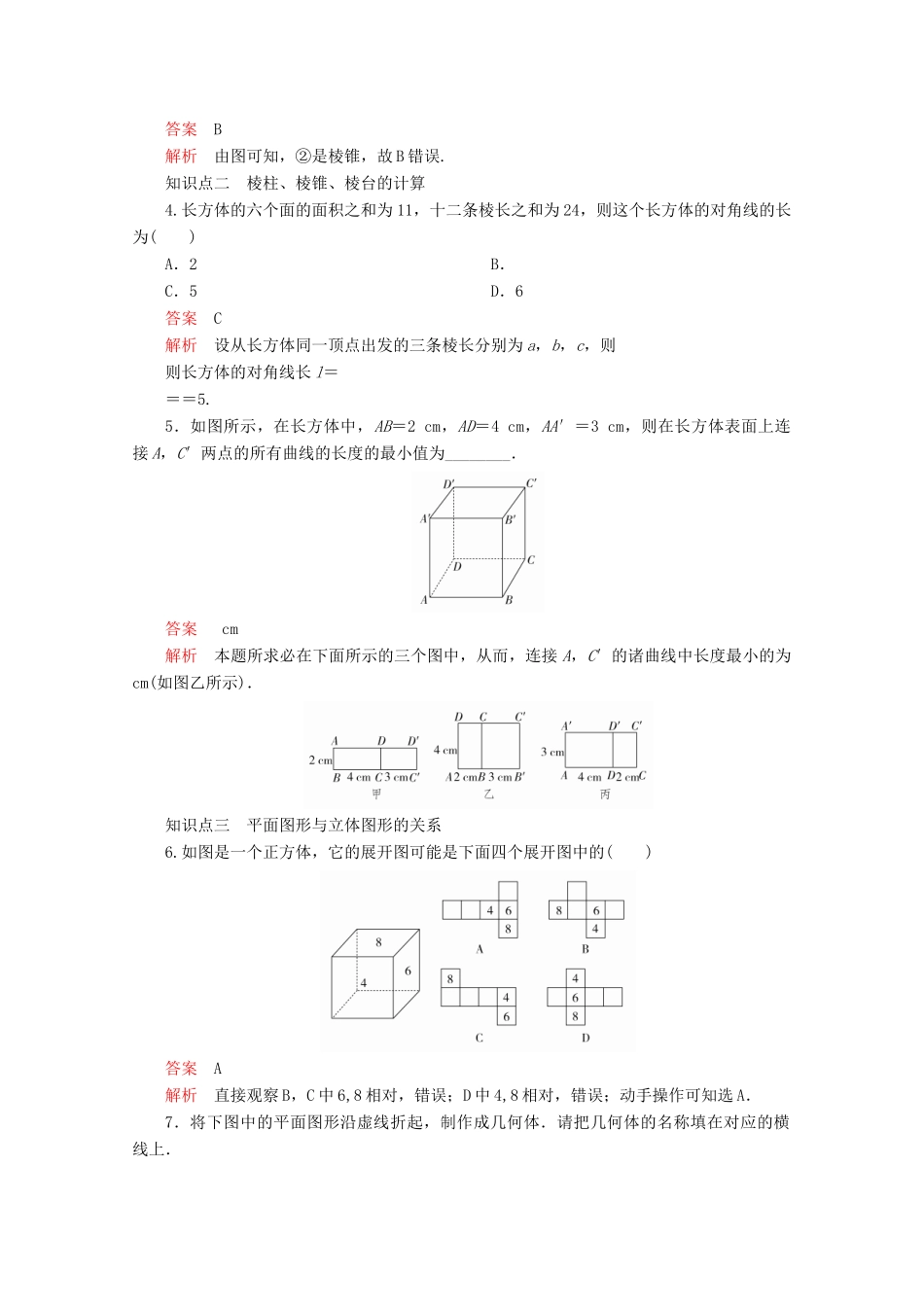
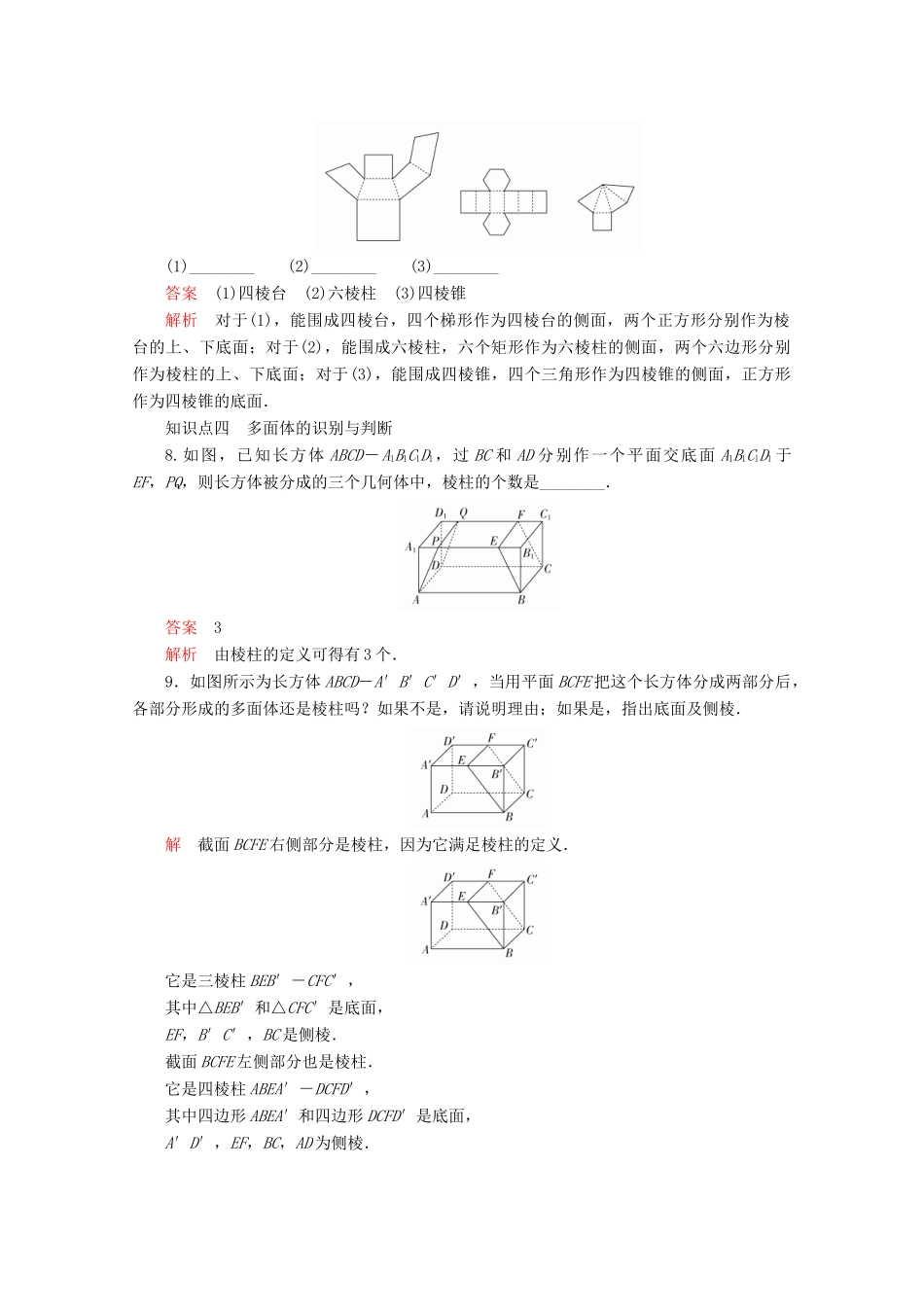
课时作业22棱柱、棱锥、棱台知识点一对棱柱、棱锥、棱台概念的理解1.下列叙述正确的是()A.有两个面互相平行,其余各面都是四边形的几何体叫棱柱B.有两个面互相平行,其余各面都是平行四边形的几何体叫棱柱C.有一个面是多边形,其余各面都是三角形的几何体叫棱锥D.棱台各侧棱的延长线交于一点答案D解析A项,没有满足棱柱各侧棱平行的条件,故A项错误;B项,一个长方体上面叠加一个各侧面与长方体各侧面都不在一个面,且底面相同的斜棱柱,则满足题目条件,但不是棱柱,故B项错误;C项,不满足各侧面三角形有公共顶点,故C项错误;D项,棱台各侧棱的延长线交于一点,故D项正确,故选D.2.下列命题中,正确的是()A.四棱柱是平行六面体B.直平行六面体是长方体C.六个面都是矩形的六面体是长方体D.底面是矩形的四棱柱是长方体答案C解析由棱柱的定义可以知道,所有棱柱的侧面四边形都是平行四边形,但底面多边形可以是任意凸多边形,即四棱柱的底面只是一个四边形,而平行六面体则要求底面是一个平行四边形;直平行六面体是在平行六面体的基础上,对侧棱有了与底面垂直的要求,但底面仍可以不是矩形;底面是矩形的四棱柱中,其侧棱不一定垂直于底面,故选C.3.观察如图所示的四个几何体,其中判断不正确的是()A.①是棱柱B.②不是棱锥C.③不是棱锥D.④是棱台答案B解析由图可知,②是棱锥,故B错误.知识点二棱柱、棱锥、棱台的计算4.长方体的六个面的面积之和为11,十二条棱长之和为24,则这个长方体的对角线的长为()A.2B.C.5D.6答案C解析设从长方体同一顶点出发的三条棱长分别为a,b,c,则则长方体的对角线长l===5.5.如图所示,在长方体中,AB=2cm,AD=4cm,AA′=3cm,则在长方体表面上连接A,C′两点的所有曲线的长度的最小值为________.答案cm解析本题所求必在下面所示的三个图中,从而,连接A,C′的诸曲线中长度最小的为cm(如图乙所示).知识点三平面图形与立体图形的关系6.如图是一个正方体,它的展开图可能是下面四个展开图中的()答案A解析直接观察B,C中6,8相对,错误;D中4,8相对,错误;动手操作可知选A.7.将下图中的平面图形沿虚线折起,制作成几何体.请把几何体的名称填在对应的横线上.(1)________(2)________(3)________答案(1)四棱台(2)六棱柱(3)四棱锥解析对于(1),能围成四棱台,四个梯形作为四棱台的侧面,两个正方形分别作为棱台的上、下底面;对于(2),能围成六棱柱,六个矩形作为六棱柱的侧面,两个六边形分别作为棱柱的上、下底面;对于(3),能围成四棱锥,四个三角形作为四棱锥的侧面,正方形作为四棱锥的底面.知识点四多面体的识别与判断8.如图,已知长方体ABCD-A1B1C1D1,过BC和AD分别作一个平面交底面A1B1C1D1于EF,PQ,则长方体被分成的三个几何体中,棱柱的个数是________.答案3解析由棱柱的定义可得有3个.9.如图所示为长方体ABCD-A′B′C′D′,当用平面BCFE把这个长方体分成两部分后,各部分形成的多面体还是棱柱吗?如果不是,请说明理由;如果是,指出底面及侧棱.解截面BCFE右侧部分是棱柱,因为它满足棱柱的定义.它是三棱柱BEB′-CFC′,其中△BEB′和△CFC′是底面,EF,B′C′,BC是侧棱.截面BCFE左侧部分也是棱柱.它是四棱柱ABEA′-DCFD′,其中四边形ABEA′和四边形DCFD′是底面,A′D′,EF,BC,AD为侧棱.一、选择题1.能保证棱锥是正棱锥的是()A.底面为正多边形B.各侧棱都相等C.侧面与底面都是全等的正三角形D.各侧面都是等腰三角形答案C解析由正棱锥的定义逐一判断.2.如右图是一个简单多面体的表面展开图(沿图中虚线折叠即可还原),则这个多面体的顶点个数为()A.6B.7C.8D.9答案B解析此多面体如下图所示.故这个多面体的顶点个数为7.3.关于几何体ABC-A1B1C1,平面ABC与平面A1B1C1平行,其中能构成棱台的是()A.AB=1,AC=2,BC=2,A1B1=2,A1C1=2,B1C1=2B.AB=1,AC=2,BC=2,A1B1=3,A1C1=4,B1C1=4C.AB=1,AC=2,BC=2,A1B1=2,A1C1=4,B1C1=4D.AB=2,AC=4,BC=3,A1B1=5,A1C1=3,B1C1=4答案C解析 A中=≠,B中≠,D中≠≠,只有C中===,∴只有C能构成棱...