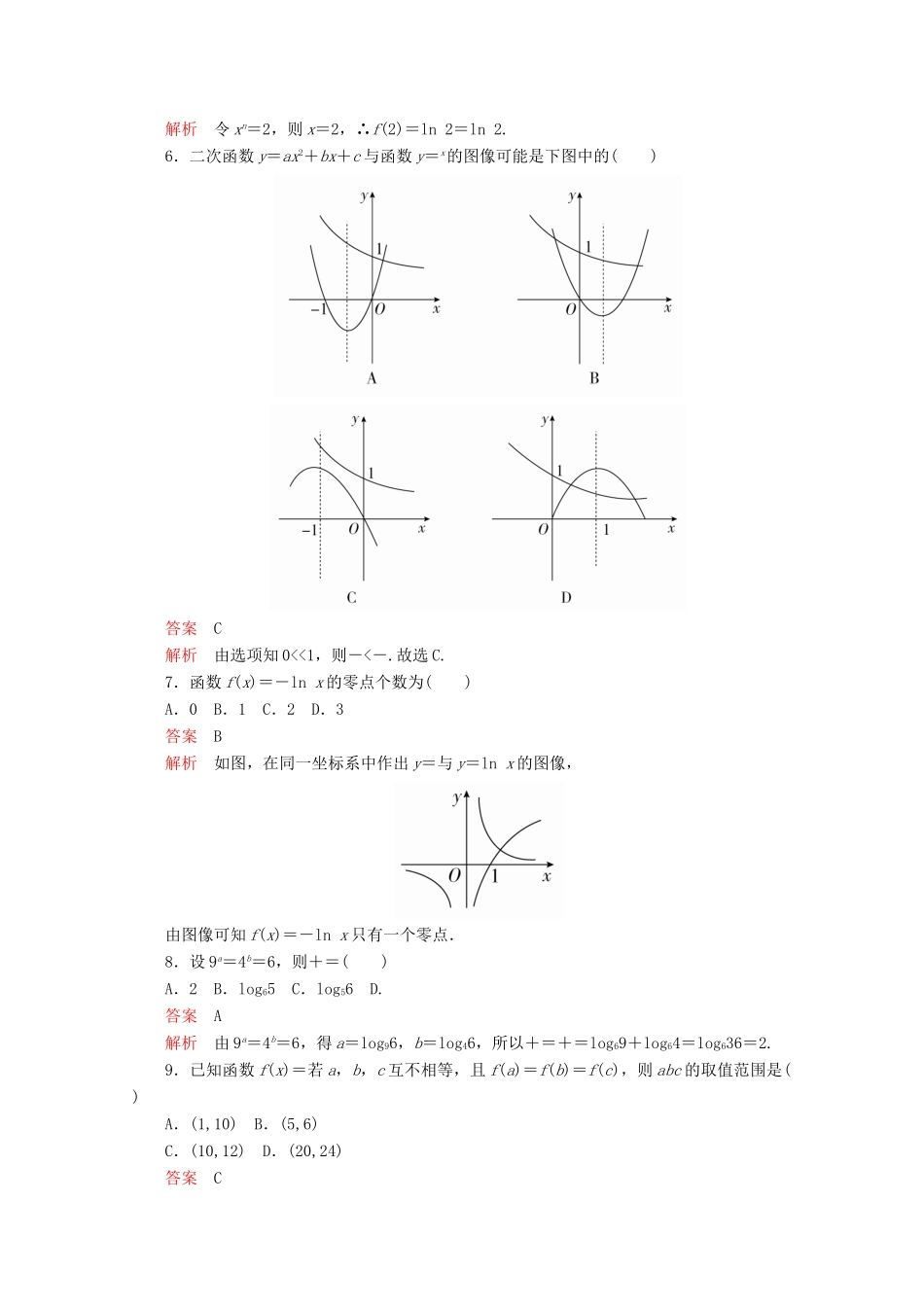
第四章指数、对数函数与幂函数单元质量测评本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.函数y=的定义域是()A.[1,+∞)B.C.D.答案D解析若使函数有意义,则必有log(3x-2)≥0,3x-2>0,即0<3x-2≤1⇒0且a≠1,下列四组函数中表示相等函数的是()A.y=logax与y=(logxa)-1B.y=alogax与y=xC.y=2x与y=logaa2xD.y=logax2与y=2logax答案C解析选项A中函数y=logax的定义域为(0,+∞),函数y=(logxa)-1的定义域为(0,1)∪(1,+∞),故不选;选项B中函数y=alogax的定义域为(0,+∞),函数y=x的定义域为R,故不选;选项C中,函数y=2x的定义域为R,函数y=logaa2x可化为y=2x,且定义域也为R,选C;选项D中函数y=logax2的定义域为{x|x≠0},函数y=2logax的定义域为(0,+∞),故不选,所以本题应选C.4.函数f(x)=x3-1在区间[1,m]上的平均变化率为7,则m的值为()A.2B.3C.4D.5答案A解析根据题意,函数f(x)=x3-1在区间[1,m]上的平均变化率为==m2+m+1,则有m2+m+1=7,即m2+m-6=0,解得m=-3或m=2,又由m>1,则m=2.故选A.5.已知f(xn)=lnx,则f(2)的值是()A.ln2B.ln2C.ln2D.2ln2答案B解析令xn=2,则x=2,∴f(2)=ln2=ln2.6.二次函数y=ax2+bx+c与函数y=x的图像可能是下图中的()答案C解析由选项知0<<1,则-<-.故选C.7.函数f(x)=-lnx的零点个数为()A.0B.1C.2D.3答案B解析如图,在同一坐标系中作出y=与y=lnx的图像,由图像可知f(x)=-lnx只有一个零点.8.设9a=4b=6,则+=()A.2B.log65C.log56D.答案A解析由9a=4b=6,得a=log96,b=log46,所以+=+=log69+log64=log636=2.9.已知函数f(x)=若a,b,c互不相等,且f(a)=f(b)=f(c),则abc的取值范围是()A.(1,10)B.(5,6)C.(10,12)D.(20,24)答案C解析设a<b<c,由f(a)=f(b)=f(c),得|lga|=|lgb|. a,b,c互不相等,∴lga=-lgb.∴ab=1.作出函数f(x)的图像如图所示,由图像可知10<c<12,∴10<abc<12.10.下列函数中,随着x的增长,增长速度最快的是()A.y=50B.y=1000xC.y=0.4·2x-1D.y=ex答案D解析指数函数y=ax在a>1时呈爆炸式增长,而且底数a越大,增长速度越快.故选D.11.设函数f(x)=ln(1+x)-ln(1-x),则f(x)是()A.奇函数,且在(0,1)上是增函数B.奇函数,且在(0,1)上是减函数C.偶函数,且在(0,1)上是增函数D.偶函数,且在(0,1)上是减函数答案A解析函数f(x)的定义域为(-1,1),f(-x)=ln(1-x)-ln(1+x)=-f(x),故f(x)为奇函数.当0<x<1时,y=ln(1+x)是增函数,y=ln(1-x)是减函数,故f(x)=ln(1+x)-ln(1-x)在(0,1)上是增函数.故选A.12.设函数f(x)=则满足f[f(a)]=2f(a)的a的取值范围是()A.B.[0,1]C.D.[1,+∞)答案C解析因为y=2x与y=3x-1在(-∞,1)上没有公共点,故由f[f(a)]=2f(a)可得f(a)≥1,故有或解得a的取值范围是.故选C.第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上)13.若a=log43,则2a+2-a=________.答案解析由a=log43得4a=3⇒2a=,则2a+2-a=+=.14.若函数f(x)=(a>0,且a≠1)的值域是[4,+∞),则实数a的取值范围是________.答案(1,2]解析当x≤2时,y=-x+6≥4,依题意得解得1<a≤2,即实数a的取值范围是(1,2].15.有以下结论:①函数y=log2(1-x)的增区间是(-∞,1);②若幂函数y=f(x)的图像经过点(2,),则该函数为偶函数;③函数y=3|x|的值域是[1,+∞).其中正确结论的序号是________(把所有正确结论的序号都填上).答案③解析①中令u=1-x,则y=log2u,根据复合函数的单调性可判断①错误;② =2α,∴α=,∴y=x,x∈[0,+∞),不具有奇偶性,故②错误;③中|x|≥0,...