3.2.2对数函数A级基础巩固1.函数f(x)=+lg(x+1)的定义域是()A.(-∞,-1)B.(1,+∞)C.(-1,1)∪(1,+∞)D.(-∞,+∞)解析:⇒x>-1且x≠1.答案:C2.函数f(x)=log2(3x+1)的值域为()A.(0,+∞)B.[0,+∞)C.[1,+∞)D.(1,+∞)解析:因为3x>0,所以3x+1>1.故log2(3x+1)>0.答案:A3.设a=log54,b=(log53)2,c=log45,则()A.a
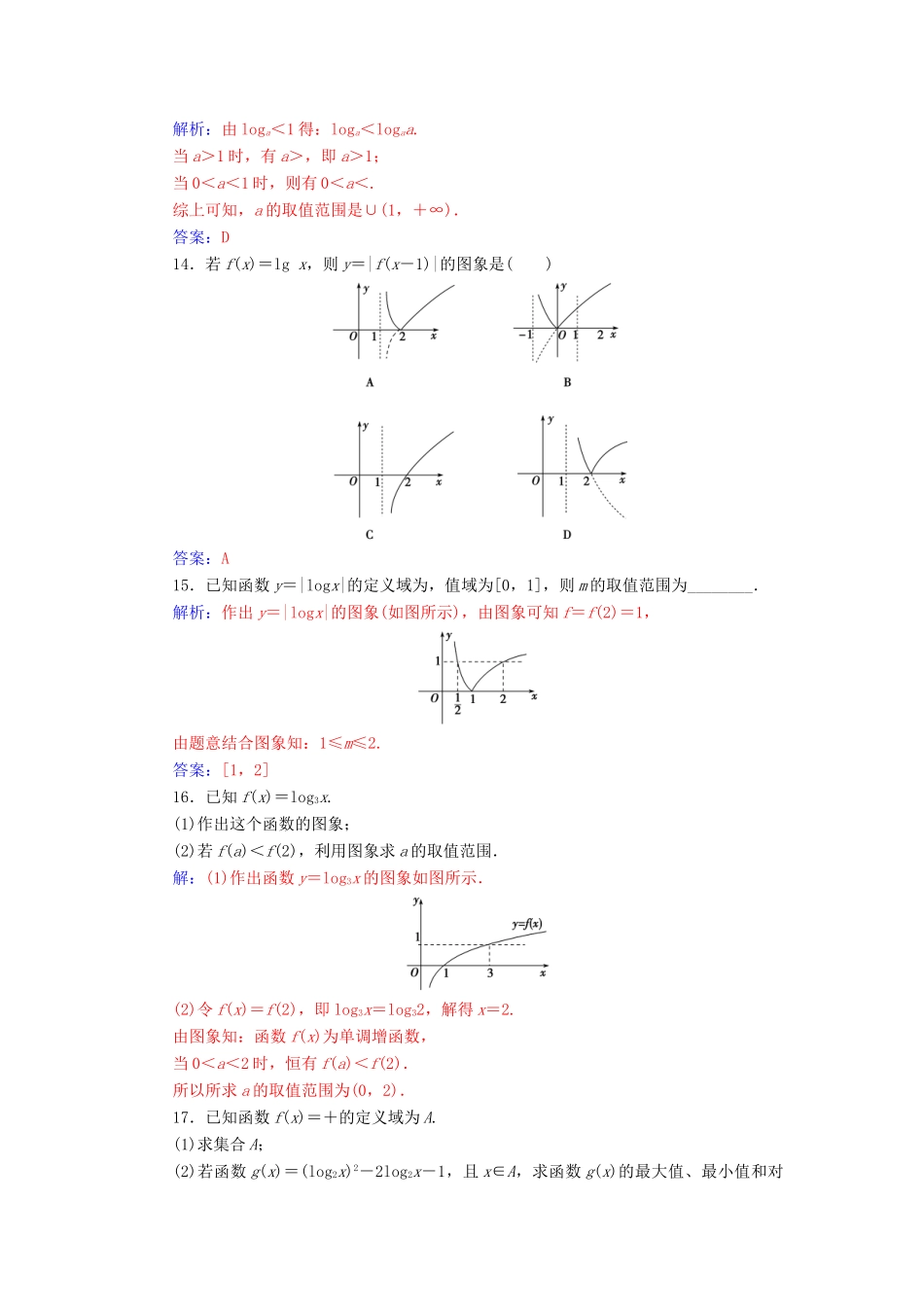
1.答案:D4.已知函数f(x)=那么f的值为()A.27B.C.-27D.-解析:f=log2=log22-3=-3,故f=f(-3)=3-3=.答案:B5.点(2,4)在函数f(x)=logax的反函数的图象上,则f=()A.-2B.2C.-1D.1解析:因为函数f(x)=logax的反函数为f-1(x)=ax,又点(2,4)在函数f-1(x)=ax的图象上.所以4=a2,则a=2.所以f(x)=log2x.故f=log2=-1.答案:C6.下列函数中,在(0,2)上为增函数的是()A.y=log(x+1)B.y=log2C.y=log2D.y=log(x2-4x+5)解析:选项A,C中函数为减函数,(0,2)不是选项B中函数的定义域.选项D中,函数y=x2-4x+5在(0,2)上为减函数,又<1,故y=log(x2-4x+5)在(0,2)上为增函数.答案:D7.已知对数函数f(x)的图象过点(8,-3),则f(2)=________.解析:设f(x)=logax(a>0,且a≠1),则-3=loga8,所以a=.所以f(x)=logx,f(2)=log(2)=-log2(2)=-.答案:-8.若定义在区间(-1,0)内的函数f(x)=log2a(x+1)满足f(x)>0,则a的取值范围是________.解析:因为-1<x<0,所以0<x+1<1.由对数函数的性质,且f(x)=log2a(x+1)>0.所以0<2a<1,解得0<a<.答案:9.已知函数f(x)=lg(2x-b)(x≥1)的值域是[0,+∞),则b的值为________.解析:由于f(x)=lg(2x-b)在[1,+∞)上是增函数,又f(x)的值域为[0,+∞),所以f(1)=lg(2-b)=0,所以2-b=1,故b=1.答案:110.若a>1,函数f(x)=logax在区间[a,2a]上的最大值与最小值之差为,则实数a的值为________.解析:因为a>1,所以f(x)=logax在(0,+∞)上是增函数.所以最大值为f(2a),最小值为f(a).所以f(2a)-f(a)=loga2a-logaa=,即loga2=.所以a=4.答案:411.已知函数y=loga(x+3)-(a>0,a≠1)的图象恒过定点A,若点A也在函数f(x)=3x+b的图象上,求b的值.解:当x+3=1,即x=-2时,对任意的a>0,且a≠1都有y=loga1-=-.所以函数y=loga(x+3)-的图象恒过定点A.若点A也在函数f(x)=3x+b的图象上,则-=3-2+b,所以b=-1.12.已知函数f(x)=log2(2+x2).(1)判断f(x)的奇偶性;(2)求函数f(x)的值域.解:(1)易知f(x)的定义域为R,且f(-x)=log2[2+(-x)2]=log2(2+x2)=f(x),所以f(x)=log2(2+x2)为偶函数.(2)对任意x∈R,t=2+x2≥2,又y=log2t在[2,+∞)上是增函数,所以1≤y.故f(x)的值域为[1,+∞).B级能力提升13.若loga<1,则a的取值范围是()A.B.C.D.∪(1+∞)解析:由loga<1得:loga<logaa.当a>1时,有a>,即a>1;当0<a<1时,则有0<a<.综上可知,a的取值范围是∪(1,+∞).答案:D14.若f(x)=lgx,则y=|f(x-1)|的图象是()答案:A15.已知函数y=|logx|的定义域为,值域为[0,1],则m的取值范围为________.解析:作出y=|logx|的图象(如图所示),由图象可知f=f(2)=1,由题意结合图象知:1≤m≤2.答案:[1,2]16.已知f(x)=log3x.(1)作出这个函数的图象;(2)若f(a)<f(2),利用图象求a的取值范围.解:(1)作出函数y=log3x的图象如图所示.(2)令f(x)=f(2),即log3x=log32,解得x=2.由图象知:函数f(x)为单调增函数,当0<a<2时,恒有f(a)<f(2).所以所求a的取值范围为(0,2).17.已知函数f(x)=+的定义域为A.(1)求集合A;(2)若函数g(x)=(log2x)2-2log2x-1,且x∈A,求函数g(x)的最大值、最小值和对应的x值.解:(1)所以所以≤x≤4,所以集合A=.(2)设t=log2x.因为x∈,所以t∈[-1,2].所以y=t2-2t-1,t∈[-1,2].因为y=t2-2t-1的对称轴为t=1∈[-1,2],所以当t=1时,y有最小值-2.所以当t=-1时,y有最大值2.所以当x=2时,g(x)的最小值为-2.当x=时,g(x)的最大值为2.18.已知函数f(x)=lg(3x-3).(1)求函数f(x)的定义域和值域;(2)设函数h(x)=f(x)-lg(3x+3),若不等式子h(x)>t无解,求实数t的取值范围.解:(1)由3x-3>0得x>1,所以定义域为(1,+∞).因为(3x-3)∈(0,+∞),所以值域为R.(2)因为h(x)=lg(3x-3)-lg(3x+3)=lg=lg的定义域为(1,+∞),且在(1,+∞)上是增函数,所以函数h(x)的值域为(-∞,0).若不等式h(x)>t无解,则t的取值范围是t≥0.