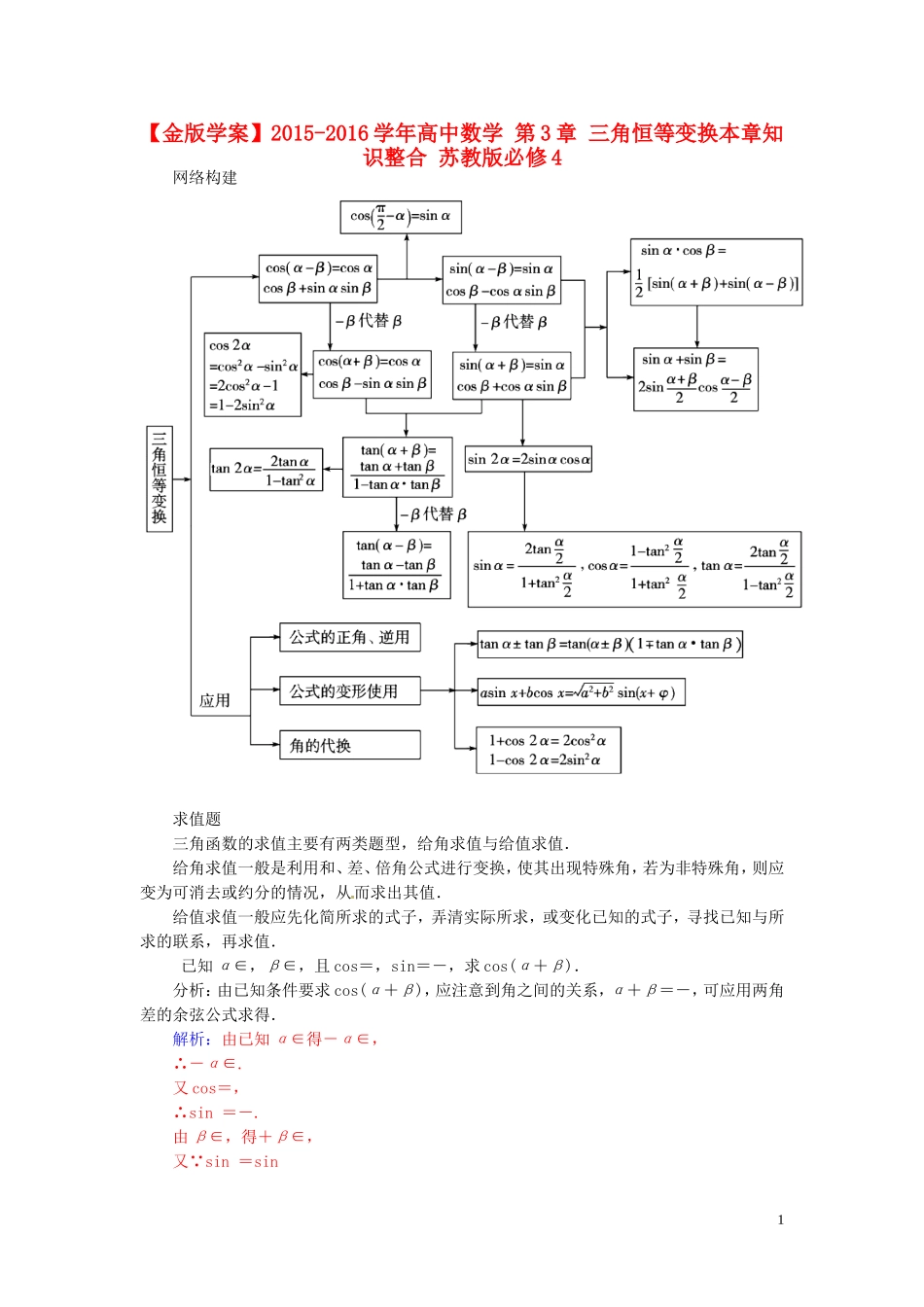
【金版学案】2015-2016学年高中数学第3章三角恒等变换本章知识整合苏教版必修4网络构建求值题三角函数的求值主要有两类题型,给角求值与给值求值.给角求值一般是利用和、差、倍角公式进行变换,使其出现特殊角,若为非特殊角,则应变为可消去或约分的情况,从而求出其值.给值求值一般应先化简所求的式子,弄清实际所求,或变化已知的式子,寻找已知与所求的联系,再求值.已知α∈,β∈,且cos=,sin=-,求cos(α+β).分析:由已知条件要求cos(α+β),应注意到角之间的关系,α+β=-,可应用两角差的余弦公式求得.解析:由已知α∈得-α∈,∴-α∈.又cos=,∴sin=-.由β∈,得+β∈,又 sin=sin1=-sin=-,∴sin=.∴cos=.由-=α+β,得cos(α+β)=cos=coscos+sin·sin=×+×=-.◎规律总结:给值求值的关键是找出已知式与欲求式之间的差异,一般可以适当变换已知式,求得另外函数式的值,以备应用,同时也要变换欲求式,便于将已知式求得的函数值代入,从而达到解题的目的.1.已知cos(α+β)=,cos(α-β)=,求tanα·tanβ的值.解析: cos(α+β)=cosαcosβ-sinαsinβ=,①cos(α-β)=cosαcosβ+sinαsinβ=,②①+②得cosαcosβ=,②-①得sinαsinβ=-,∴tanαtanβ===-.求sin220°+cos280°+sin20°cos80°的值.解析:方法一原式=(1-cos40°)+(1+cos160°)+·(sin100°-sin60°)=1+(cos160°-cos40°)+sin100°-=-sin100°sin60°+sin100°=.方法二原式=sin220°+cos2(60°+20°)+sin20°·cos(60°+20°)=sin220°++sin20°·=sin220°+cos220°=.方法三令M=sin220°+cos280°+sin20°cos80°,则其对偶式N=cos220°+sin280°+cos20°sin80°.因为M+N=(sin220°+cos220°)+(cos280°+sin280°)+·(sin20°cos80°+cos20°sin80°)=2+sin100°,①M-N=(sin220°-cos220°)+(cos280°-sin280°)+(sin20°cos80°-cos20°sin80°)=-cos40°+cos160°-sin60°=-2sin100°sin60°-=-sin100°-,②所以①+②得2M=,M=,即sin220°+cos280°+sin20°cos80°的值为.◎规律总结:“给角求值”问题,一般所给出的角都是非特殊角,从表面上看是很难的,但仔细观察非特殊角与特殊角总有一定的关系,解题时,要认真观察,综合三角公式转化为特殊角并且清除非特殊角的三角函数而得解.22.求的值.解析:原式======-4.一元二次方程mx2+(2m-3)x+(m-2)=0的两根为tanα,tanβ.求tan(α+β)的最小值.解析: mx2+(2m-3)x+m-2=0有两根tanα,tanβ,∴解得m≤且m≠0.由一元二次方程的根与系数的关系得tanα+tanβ=,tanα·tanβ=.∴tan(α+β)====-m≥-=-.故tan(α+β)的最小值为-.◎规律总结:数学问题解决的过程实质上是一个等价转化的过程,这一点务必引起高度重视.特别是综合题,条件的使用顺序和转化,以及知识之间的联系,在平时的训练中都要认真体会和总结.3.如下图,三个相同的正方形相接,试计算α+β的大小.解析:本题的实质是已知tanα=,tanβ=,且α,β∈,求α+β.可通过求tan(α+β)及(α+β)的范围来求得α+β.由图可知:tanα=,tanβ=且α,β均为锐角.∴tan(α+β)===1.而α+β∈(0,π),在(0,π)上正切值等于1的角只有,∴α+β=.规律总结:已知三角函数值求角,分三步进行:①先求角α+β的某一三角函数值;②确定角所在范围(或区间);③求角的值.化简三角函数式的化简是三角变换应用的一个重要方面,其基本思想方法是统一角,统一三角函数的名称.在具体实施过程中,应着重抓住“角”的统一.通过观察角、函数名、项的次数等,找到突破口,利用切化弦、升幂、降幂、逆用公式等手段将其化简.最后结果要求:(1)能求值尽量求值;(2)三角函数名称尽量少;(3)项数尽量少;(4)次数尽量低;(5)分母、根号下尽量不含三角函数.化简:tan70°cos10°·(tan20°-1).3分析:先化切为弦,再利用特殊角的特殊值进行转换.解析:tan70°cos10°·(tan20°-1)=·cos10°·=co...