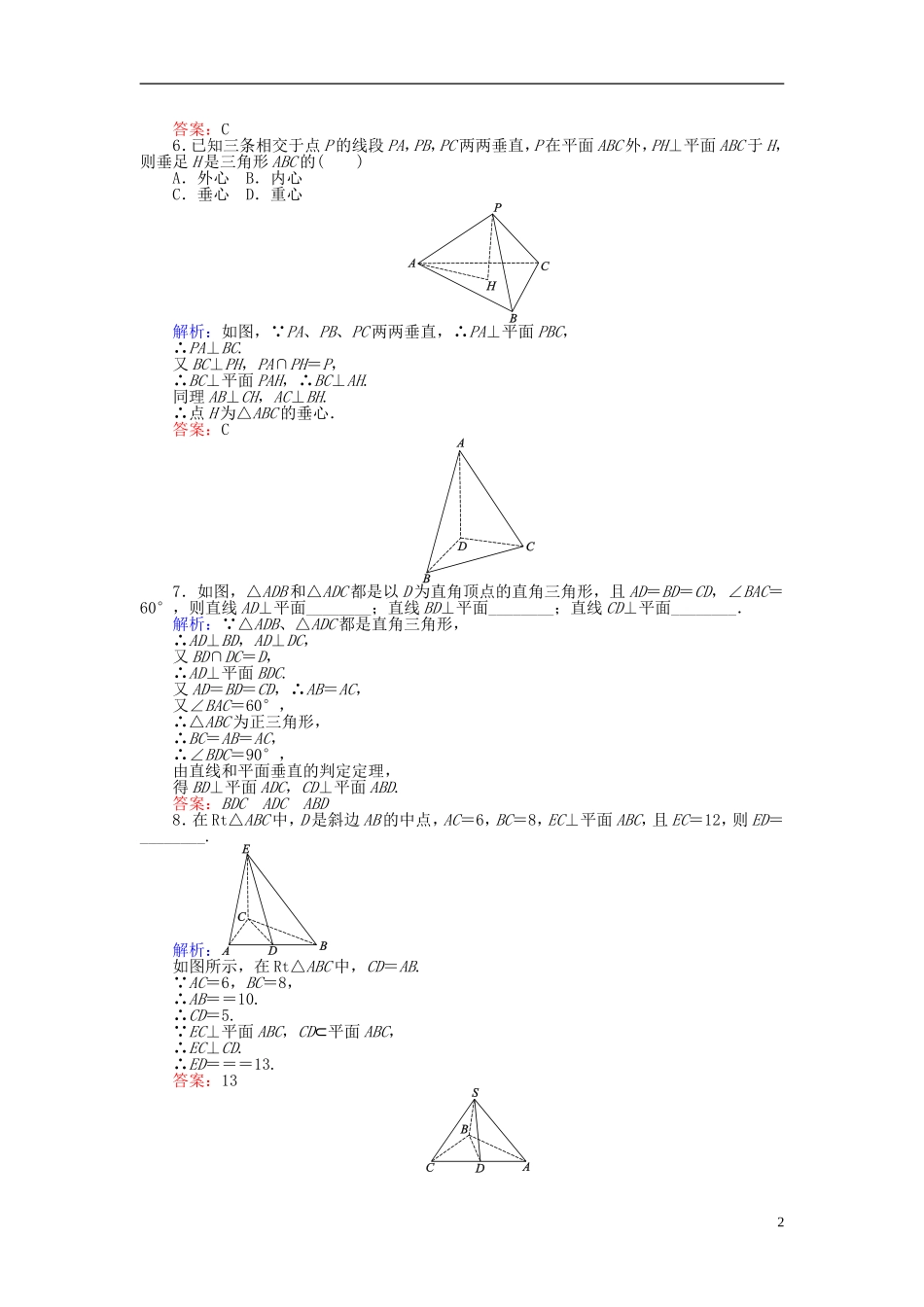
课时作业(十二)直线与平面垂直的判定A组基础巩固1.空间四边形ABCD的四边相等,则它的两对角线AC、BD的关系是()A.垂直且相交B.相交但不一定垂直C.垂直但不相交D.不垂直也不相交解析:取BD的中点E,连接AE,CE.可证BD⊥AE,BD⊥CE,而AE∩CE=E,即得BD⊥平面AEC.得BD⊥AC.故选C.答案:C2.正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总保持AP⊥BD1,则动点P的轨迹是()A.线段B1CB.线段BC1C.BB1中点与CC1中点连成的线段D.BC中点与B1C1中点连成的线段解析:如图,由于BD1⊥平面AB1C,故点P一定位于B1C上.答案:A3.在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,M是棱PC上一点.若PA=AC=a,则当△MBD的面积为最小值时,直线AC与平面MBD所成的角为()A.B.C.D.解析:因为PA⊥底面ABCD,则PA⊥AC,又PA=AC,∴∠PCA=45°,因△PAB≌△PAD⇒PB=PD,又△PBM≌△PDM⇒BM=DM,设AC与BD交于0,则OM⊥BD,S△MCD=BD·OM最小,只需OM最短,过O作OM′⊥PC,垂足为M′,连接M′B、M′A,此时直线AC与平面M′BD所成的角为∠CM′O=.答案:B4.如图,四棱锥P-ABCD中,PA⊥平面ABCD,则PD与平面ABCD所成的角为图中的()A.∠PADB.∠PDAC.∠PDBD.∠PDC解析: PA⊥平面ABCD,∴AD是PD在平面ABCD上的射影,故∠PDA是PD与平面ABCD所成的角.答案:B5.若斜线段AB是它在平面α内的射影长的2倍,则AB与平面α所成角为()A.30°B.45°C.60°D.120°解析:设AB与平面α所成的角为θ,由题意可知cosθ=,∴θ=60°.1答案:C6.已知三条相交于点P的线段PA,PB,PC两两垂直,P在平面ABC外,PH⊥平面ABC于H,则垂足H是三角形ABC的()A.外心B.内心C.垂心D.重心解析:如图, PA、PB、PC两两垂直,∴PA⊥平面PBC,∴PA⊥BC.又BC⊥PH,PA∩PH=P,∴BC⊥平面PAH,∴BC⊥AH.同理AB⊥CH,AC⊥BH.∴点H为△ABC的垂心.答案:C7.如图,△ADB和△ADC都是以D为直角顶点的直角三角形,且AD=BD=CD,∠BAC=60°,则直线AD⊥平面________;直线BD⊥平面________;直线CD⊥平面________.解析: △ADB、△ADC都是直角三角形,∴AD⊥BD,AD⊥DC,又BD∩DC=D,∴AD⊥平面BDC.又AD=BD=CD,∴AB=AC,又∠BAC=60°,∴△ABC为正三角形,∴BC=AB=AC,∴∠BDC=90°,由直线和平面垂直的判定定理,得BD⊥平面ADC,CD⊥平面ABD.答案:BDCADCABD8.在Rt△ABC中,D是斜边AB的中点,AC=6,BC=8,EC⊥平面ABC,且EC=12,则ED=________.解析:如图所示,在Rt△ABC中,CD=AB. AC=6,BC=8,∴AB==10.∴CD=5. EC⊥平面ABC,CD⊂平面ABC,∴EC⊥CD.∴ED===13.答案:1329.如图所示:直角△ABC所在的平面外一点S,SA=SB=SC,点D为斜边AC的中点.则直线SD与平面ABC的位置关系为________.解析: SA=SC,点D为斜边AC的中点,∴SD⊥AC.则在Rt△ABC中,AD=DC=BD,∴△ADS≌△BDS,∴SD⊥BD.又AC∩BD=D,∴SD⊥平面ABC.答案:垂直10.如图,四棱锥P-ABCD的底面是边长为1的正方形,PD⊥BC,PD=1,PC=.求证:PD⊥平面ABCD.证明: PD=DC=1,PC=,∴PD2+DC2=PC2,∴△PDC是直角三角形.∴PD⊥CD.又 PD⊥BC,BC∩CD=C,且BC⊂平面ABCD,CD⊂平面ABCD,∴PD⊥平面ABCD.B组能力提升11.在正方体ABCD-A1B1C1D1中,E,F分别是AA1,A1D1的中点,求:(1)D1B与平面ABCD所成角的余弦值;(2)EF与平面A1B1C1D1所成的角.解析:(1)如图所示,连接DB, D1D⊥平面ABCD,∴DB是D1B在平面ABCD内的射影.则∠D1BD即为D1B与平面ABCD所成的角. DB=AB,D1B=AB,∴cos∠D1BD==,即D1B与平面ABCD所成角的余弦值为.(2) E是A1A的中点,A1A⊥平面A1B1C1D1,∴∠EFA1是EF与平面A1B1C1D1所成的角.在Rt△EA1F中, F是A1D1的中点,∴∠EFA1=45°.12.如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC的中点,PO⊥平面ABCD,PO=2,M为PD的中点.(1)证明:PB∥平面ACM;(2)证明:AD⊥平面PAC;(3)求直线AM与平面ABCD所成角的正切值.3解析:(1)证明:如图连接BD,MO.在平行四边形ABCD中, O为AC的中点,∴O为BD的中点,又M为PD的中点,∴PB∥M...