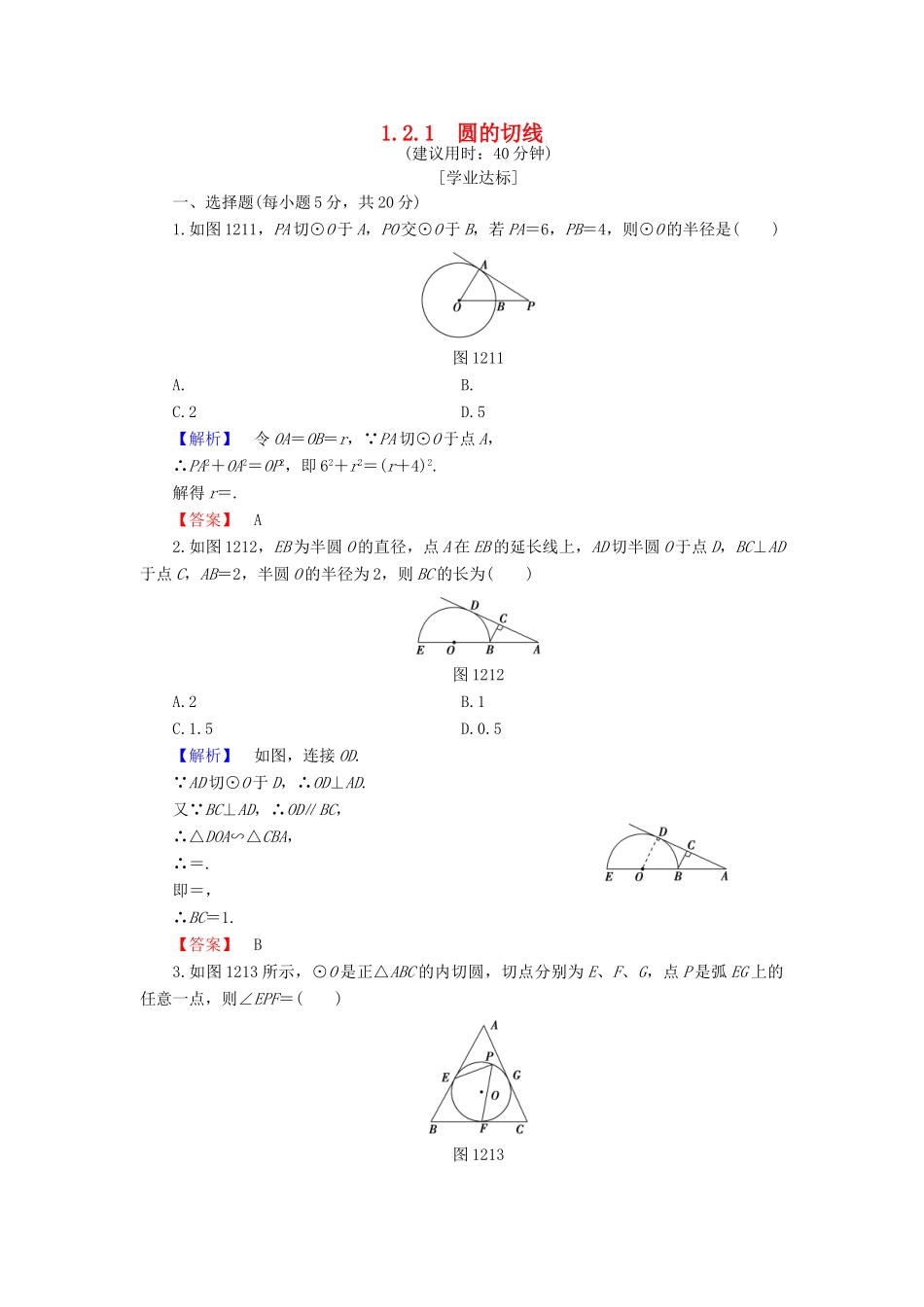
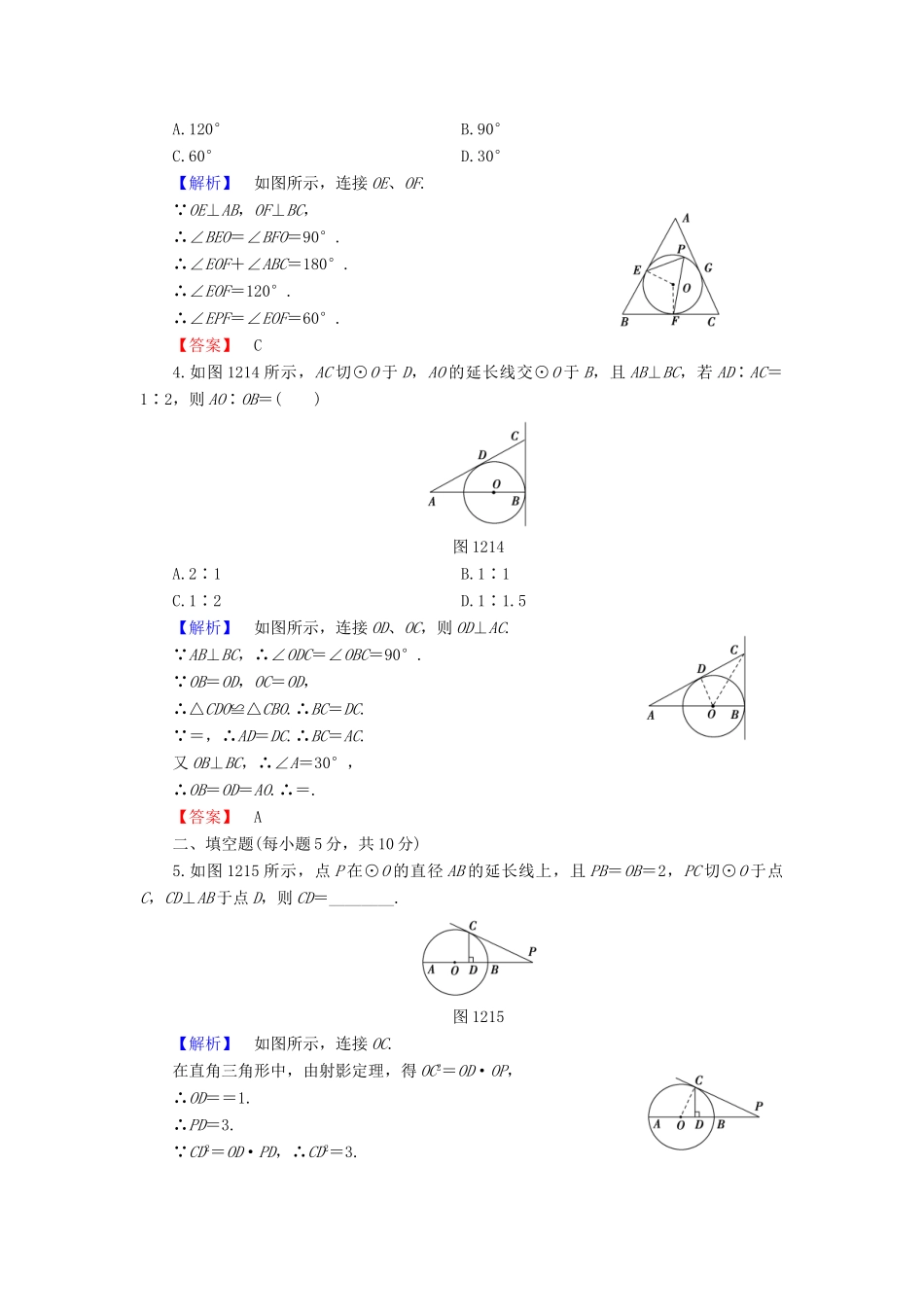
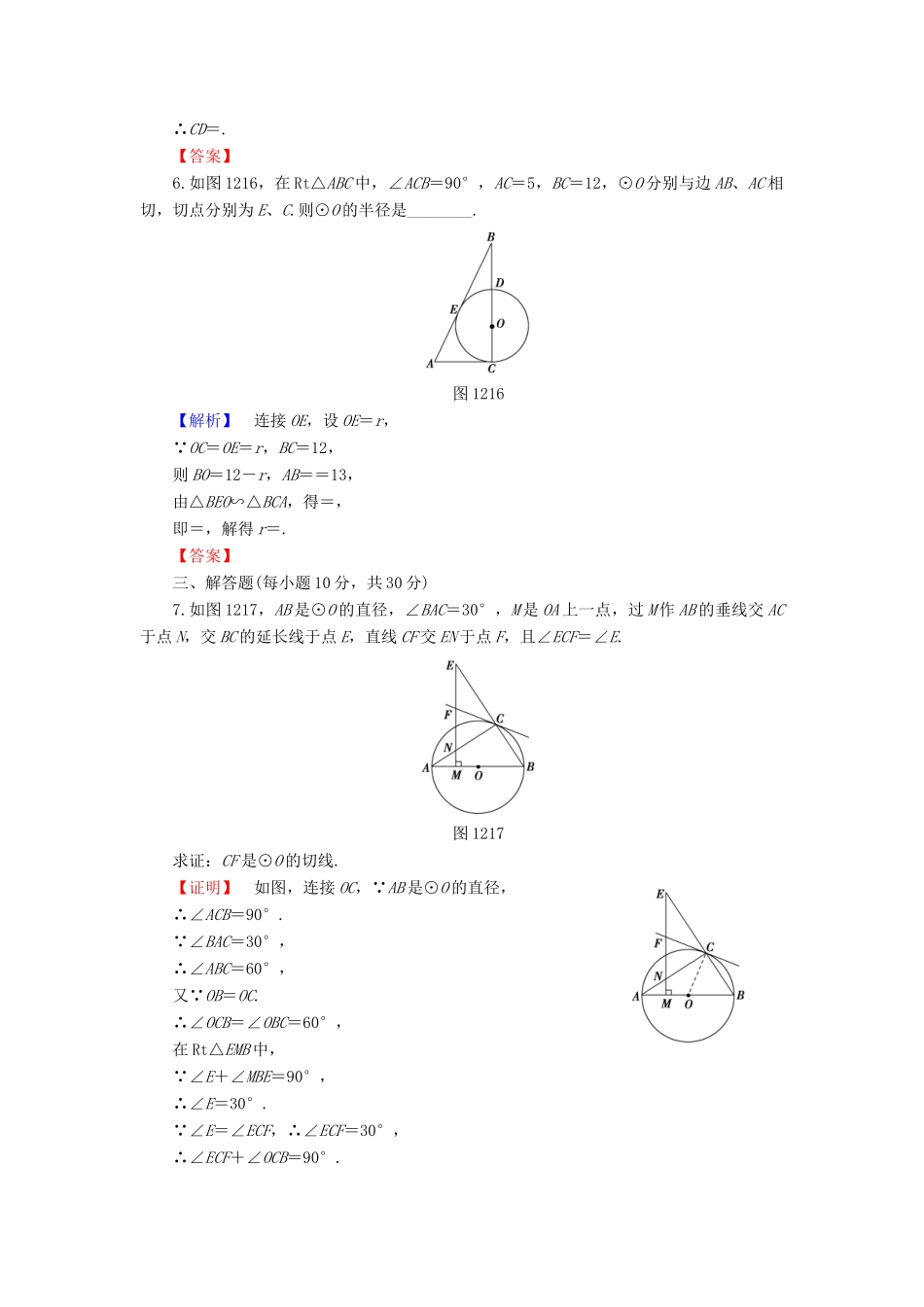
1.2.1圆的切线(建议用时:40分钟)[学业达标]一、选择题(每小题5分,共20分)1.如图1211,PA切⊙O于A,PO交⊙O于B,若PA=6,PB=4,则⊙O的半径是()图1211A.B.C.2D.5【解析】令OA=OB=r,∵PA切⊙O于点A,∴PA2+OA2=OP2,即62+r2=(r+4)2.解得r=.【答案】A2.如图1212,EB为半圆O的直径,点A在EB的延长线上,AD切半圆O于点D,BC⊥AD于点C,AB=2,半圆O的半径为2,则BC的长为()图1212A.2B.1C.1.5D.0.5【解析】如图,连接OD.∵AD切⊙O于D,∴OD⊥AD.又∵BC⊥AD,∴OD∥BC,∴△DOA∽△CBA,∴=.即=,∴BC=1.【答案】B3.如图1213所示,⊙O是正△ABC的内切圆,切点分别为E、F、G,点P是弧EG上的任意一点,则∠EPF=()图1213A.120°B.90°C.60°D.30°【解析】如图所示,连接OE、OF.∵OE⊥AB,OF⊥BC,∴∠BEO=∠BFO=90°.∴∠EOF+∠ABC=180°.∴∠EOF=120°.∴∠EPF=∠EOF=60°.【答案】C4.如图1214所示,AC切⊙O于D,AO的延长线交⊙O于B,且AB⊥BC,若AD∶AC=1∶2,则AO∶OB=()图1214A.2∶1B.1∶1C.1∶2D.1∶1.5【解析】如图所示,连接OD、OC,则OD⊥AC.∵AB⊥BC,∴∠ODC=∠OBC=90°.∵OB=OD,OC=OD,∴△CDO≌△CBO.∴BC=DC.∵=,∴AD=DC.∴BC=AC.又OB⊥BC,∴∠A=30°,∴OB=OD=AO.∴=.【答案】A二、填空题(每小题5分,共10分)5.如图1215所示,点P在⊙O的直径AB的延长线上,且PB=OB=2,PC切⊙O于点C,CD⊥AB于点D,则CD=________.图1215【解析】如图所示,连接OC.在直角三角形中,由射影定理,得OC2=OD·OP,∴OD==1.∴PD=3.∵CD2=OD·PD,∴CD2=3.∴CD=.【答案】6.如图1216,在Rt△ABC中,∠ACB=90°,AC=5,BC=12,⊙O分别与边AB、AC相切,切点分别为E、C.则⊙O的半径是________.图1216【解析】连接OE,设OE=r,∵OC=OE=r,BC=12,则BO=12-r,AB==13,由△BEO∽△BCA,得=,即=,解得r=.【答案】三、解答题(每小题10分,共30分)7.如图1217,AB是⊙O的直径,∠BAC=30°,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,且∠ECF=∠E.图1217求证:CF是⊙O的切线.【证明】如图,连接OC,∵AB是⊙O的直径,∴∠ACB=90°.∵∠BAC=30°,∴∠ABC=60°,又∵OB=OC.∴∠OCB=∠OBC=60°,在Rt△EMB中,∵∠E+∠MBE=90°,∴∠E=30°.∵∠E=∠ECF,∴∠ECF=30°,∴∠ECF+∠OCB=90°.又∵∠ECF+∠OCB+∠OCF=180°,∴∠OCF=90°.∴CF为⊙O的切线.8.如图1218,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB于E,∠POC=∠PCE.图1218(1)求证:PC是⊙O的切线;(2)若OE∶EA=1∶2,PA=6,求⊙O半径.【解】(1)证明:在△OCP与△CEP中,∵∠POC=∠PCE,∠OPC=∠CPE,∴∠OCP=∠CEP.∵CD⊥AB,∴∠CEP=90°,∴∠OCP=90°.又C点在圆上,∴PC是⊙O的切线.(2)法一设OE=x,则EA=2x,OC=OA=3x.∵∠COE=∠AOC,∠OEC=∠OCP=90°,∴△OCE∽△OPC,∴=.即(3x)2=x(3x+6),∴x=1,∴OA=3x=3,即圆的半径为3.法二由(1)知PC是⊙O的切线,∴∠OCP=90°.又∵CD⊥OP,由射影定理知OC2=OE·OP,以下同法一.[能力提升]9.如图1219,AD是⊙O的直径,BC切⊙O于点D,AB、AC与圆分别相交于点E、F.图1219(1)AE·AB与AF·AC有何关系?请给予证明;(2)在图中,如果把直线BC向上或向下平移,得到图(1)或图(2),在此条件下,(1)题的结论是否仍成立?为什么?【解】(1)AE·AB=AF·AC.证明:连接DE.∵AD为⊙O的直径,∴∠DEA=90°.又∵BC与⊙O相切于点D,∴AD⊥BC,即∠ADB=90°,∴∠ADB=∠DEA.又∵∠BAD=∠DAE,∴△BAD∽△DAE,∴=,即AD2=AB·AE.同理AD2=AF·AC,∴AE·AB=AF·AC.(2)(1)中的结论仍成立.因为BC在平移时始终与AD垂直,设垂足为D′,则∠AD′B=90°.∵AD为圆的直径,∴∠AED=∠AD′B=90°.又∵∠DAE=∠BAD′.∴△ABD′∽△ADE.∴=,∴AB·AE=AD·AD′.同理AF·AC=AD·AD′,故AE·AB=AF·AC.