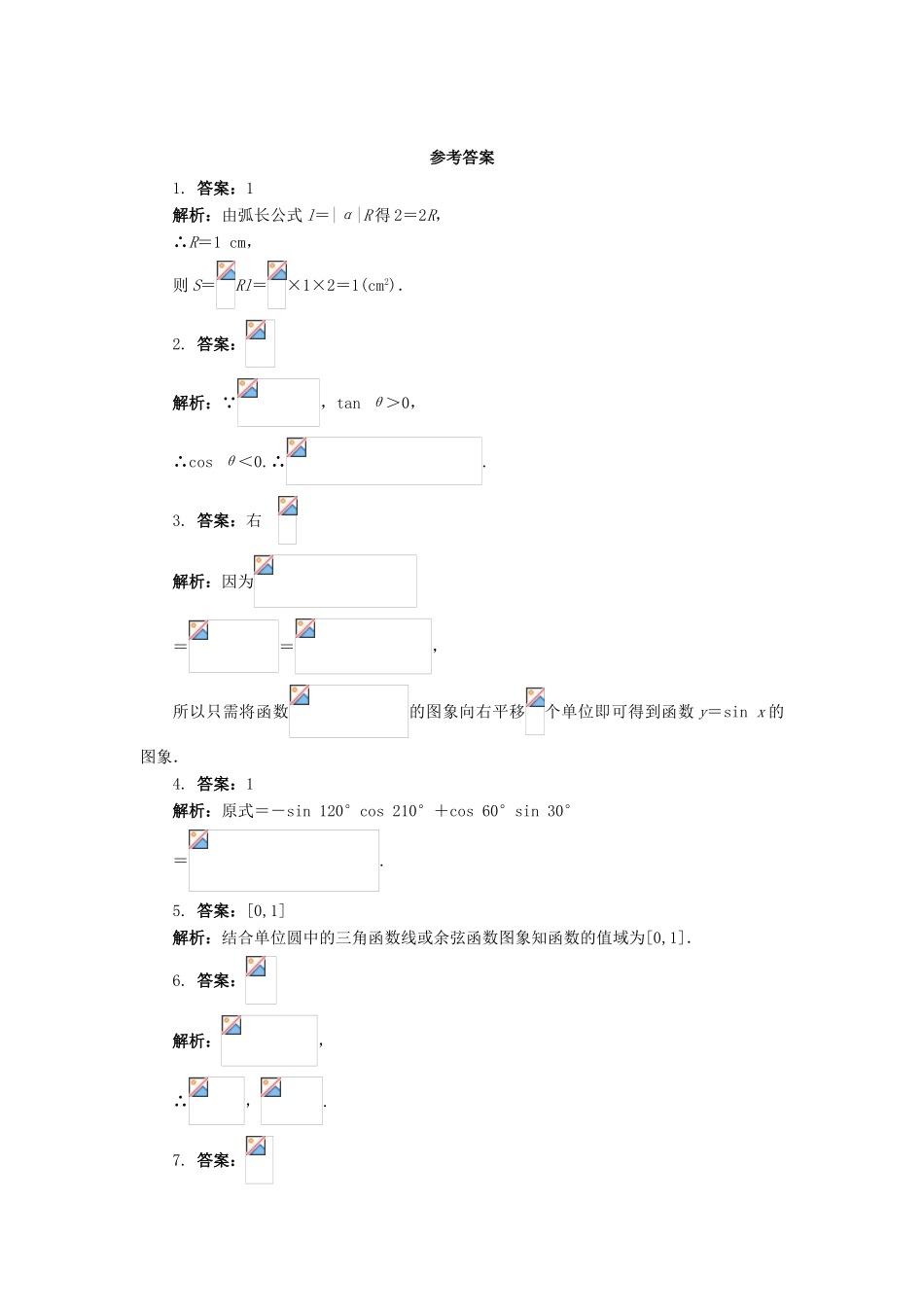
数学苏教必修4第1章三角函数单元检测(满分:100分时间:60分钟)一、填空题(本大题共10小题,每小题5分,共50分)1.若2弧度的圆心角所对的弧长为2cm,则这个圆心角所夹的扇形的面积是__________cm2.2.若,tanθ>0,则cosθ=__________.3.要得到函数y=sinx的图象,只需将函数的图象向__________平移__________个单位.4.sin(-120°)cos1290°+cos(-1020°)sin(-1050°)=__________.5.函数y=cosx,的值域是__________.6.函数的最小正周期是4π,则ω=__________.7.若,且π<x<2π,则x=__________.8.已知tanθ=2,则=__________.9.设a为常数,且a<0,0≤x<2π,则函数f(x)=cos2x-2asinx-1的最小值是__________.10.如果函数y=3cos(2x+φ)的图象关于点对称,那么|φ|的最小值为__________.二、解答题(本大题共4小题,共50分)11.(12分)若sinαcosα<0,sinαtanα<0,化简:.12.(12分)已知=,求sin3(2π-α)+cos3(2π-α)的值.13.(12分)已知函数(x∈R,a>0,ω>0)的最小正周期为π,函数f(x)的最大值是,最小值是.(1)求ω,a,b的值;(2)求f(x)的单调增区间.14.(14分)函数f1(x)=Asin(ωx+φ)的一段图象过点(0,1),如图所示.(1)求函数f1(x)的表达式;(2)将函数y=f1(x)的图象向右平移个单位,得到函数y=f2(x)的图象,求y=f2(x)的最大值,并求出此时自变量x的取值.参考答案1.答案:1解析:由弧长公式l=|α|R得2=2R,∴R=1cm,则S=Rl=×1×2=1(cm2).2.答案:解析:∵,tanθ>0,∴cosθ<0.∴.3.答案:右解析:因为==,所以只需将函数的图象向右平移个单位即可得到函数y=sinx的图象.4.答案:1解析:原式=-sin120°cos210°+cos60°sin30°=.5.答案:[0,1]解析:结合单位圆中的三角函数线或余弦函数图象知函数的值域为[0,1].6.答案:解析:,∴,.7.答案:解析:∵,∴.又π<x<2π,∴.8.答案:解析:===.9.答案:2a-1解析:f(x)=cos2x-2asinx-1=1-sin2x-2asinx-1=-sin2x-2asinx=-(sin2x+2asinx+a2-a2)=-(sinx+a)2+a2.∵a<0,∴当sinx=-1时,f(x)取得最小值.f(x)min=-(-1+a)2+a2=2a-1.10.答案:解析:∵函数y=3cos(2x+φ)的对称中心为,∴2×+φ=kπ+(k∈Z).∴φ=kπ+-(k∈Z).∴|φ|的最小值为.11.解:∵sinαcosα<0,sinαtanα<0,∴α是第二象限角,即2kπ+<α<2kπ+π(k∈Z),故kπ+<<kπ+,即是第一或第三象限角.原式==,∴当是第一象限角时,原式=;当是第三象限角时,原式=.12.解:由,得.∴1+2sinαcosα=,2sinαcosα=.∵<α<π,∴sinα>0,cosα<0.从而sinα-cosα===.于是原式=cos3α-sin3α=(cosα-sinα)(cos2α+sinαcosα+sin2α)=.13.解:(1)由函数的最小正周期为π,得=π,∴ω=1.又f(x)的最大值是,最小值是,则解得,b=1.(2)由(1)知:.当2kπ-≤2x+≤2kπ+(k∈Z),即kπ-≤x≤kπ+(k∈Z)时,f(x)单调递增,∴f(x)的单调增区间为(k∈Z).14.解:(1)由图知,T=π,于是ω==2.将y=Asin2x的图象向左平移个单位,得y=Asin(2x+φ)的图象,于是.将(0,1)代入,得A=2.故.(2)依题意,.当2x+=2kπ+π,即x=kπ+(k∈Z)时,ymax=2.此时x的取值为.