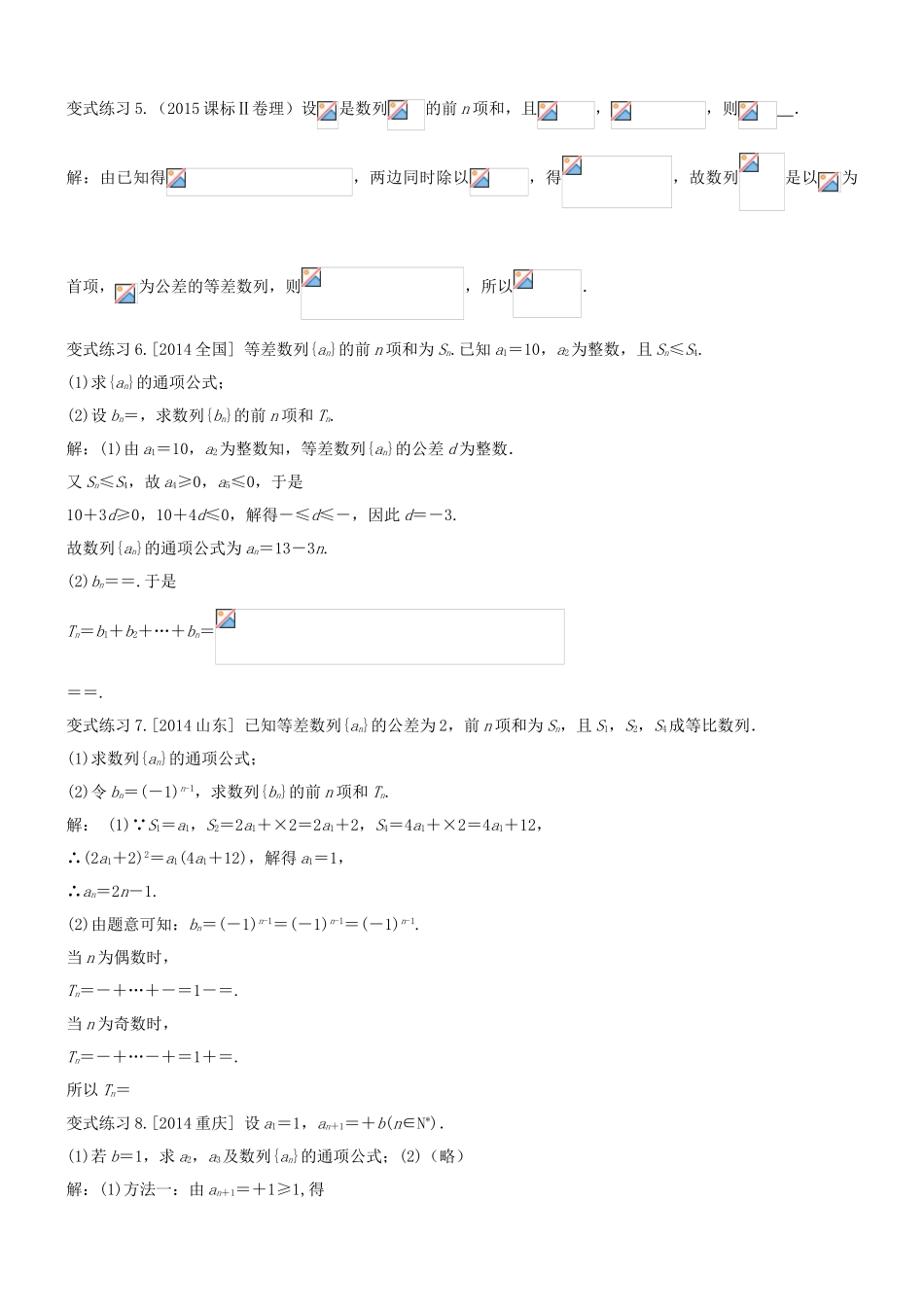
常见数列类型的通项公式的求法二、已知数列是等差(比)数列,用公式法求通项1.等差数列通项公式:(d为公差);2.等比数列通项公式:(q为公比)例2.【2016高考新课标2理数】为等差数列的前项和,且记,其中表示不超过的最大整数,如.(Ⅰ)求;(Ⅱ)求数列的前1000项和.解:(Ⅰ)设的公差为,据已知有,解得所以的通项公式为(Ⅱ)因为所以数列的前项和为例3.[2014江西]已知首项都是1的两个数列{an},{bn}(bn≠0,n∈N*)满足anbn+1-an+1bn+2bn+1bn=0.(1)令cn=,求数列{cn}的通项公式;(2)若bn=3n-1,求数列{an}的前n项和Sn.解:(1)因为anbn+1-an+1bn+2bn+1bn=0,bn≠0(n∈N*),所以-=2,即cn+1-cn=2,所以数列{cn}是以c1=1为首项,d=2为公差的等差数列,故cn=2n-1.(2)由bn=3n-1,知an=(2n-1)3n-1,于是数列{an}的前n项和Sn=1×30+3×31+5×32+…+(2n-1)×3n-1,3Sn=1×31+3×32+…+(2n-3)×3n-1+(2n-1)×3n,将两式相减得-2Sn=1+2×(31+32+…+3n-1)-(2n-1)×3n=-2-(2n-2)×3n,所以Sn=(n-1)3n+1.变式练习5.(2015课标Ⅱ卷理)设是数列的前n项和,且,,则.解:由已知得,两边同时除以,得,故数列是以为首项,为公差的等差数列,则,所以.变式练习6.[2014全国]等差数列{an}的前n项和为Sn.已知a1=10,a2为整数,且Sn≤S4.(1)求{an}的通项公式;(2)设bn=,求数列{bn}的前n项和Tn.解:(1)由a1=10,a2为整数知,等差数列{an}的公差d为整数.又Sn≤S4,故a4≥0,a5≤0,于是10+3d≥0,10+4d≤0,解得-≤d≤-,因此d=-3.故数列{an}的通项公式为an=13-3n.(2)bn==.于是Tn=b1+b2+…+bn===.变式练习7.[2014山东]已知等差数列{an}的公差为2,前n项和为Sn,且S1,S2,S4成等比数列.(1)求数列{an}的通项公式;(2)令bn=(-1)n-1,求数列{bn}的前n项和Tn.解:(1) S1=a1,S2=2a1+×2=2a1+2,S4=4a1+×2=4a1+12,∴(2a1+2)2=a1(4a1+12),解得a1=1,∴an=2n-1.(2)由题意可知:bn=(-1)n-1=(-1)n-1=(-1)n-1.当n为偶数时,Tn=-+…+-=1-=.当n为奇数时,Tn=-+…-+=1+=.所以Tn=变式练习8.[2014重庆]设a1=1,an+1=+b(n∈N*).(1)若b=1,求a2,a3及数列{an}的通项公式;(2)(略)解:(1)方法一:由an+1=+1≥1,得a2=2,a3=+1,(an+1-1)2=(an-1)2+1.从而{(an-1)2}是首项为0,公差为1的等差数列,故(an-1)2=n-1,即an=+1(n∈N*).方法二:a2=2,a3=+1.可写为a1=+1,a2=+1,a3=+1.因此猜想an=+1.下面用数学归纳法证明上式.当n=1时,结论显然成立.假设n=k时结论成立,即ak=+1,则ak+1=+1=+1=+1,这就是说,当n=k+1时结论成立.所以an=+1(n∈N*).变式练习9.(2012新课标Ⅰ(16))数列满足,则的前项和为。解法一: an+1+(﹣1)nan=2n﹣1,∴a2﹣a1=1,a3+a2=3,a4﹣a3=5,a5+a4=7,a6﹣a5=9,a7+a6=11,…,a50﹣a49=97,…从而可得a3+a1=2,a4+a2=8,a7+a5=2,a8+a6=24,a9+a11=2,a12+a10=40,a13+a11=2,a16+a14=56,…,从第一项开始,依次取2个相邻奇数项的和都等于2,从第二项开始,依次取2个相邻偶数项的和构成以8为首项,以16为公差的等差数列.∴{an}的前60项和为15×2+(15×8+)=1830,故答案为:1830.或者:可知连续四项的和构成首项是10、公差是16的等差数列,故的前项和为解法二:可证明:变式练习10.(2011全国,理20)设数列{an}满足a1=0且.(1)求{an}的通项公式;(2)设,记,证明:Sn<1.【命题意图】本题主要考查等差数列的定义及其通项公式,裂项相消法求和,不等式的证明,考查考生分析问题、解决问题的能力.解:(Ⅰ)由题设,即是公差为1的等差数列.又,故.所以……………………………5分(Ⅱ)由(Ⅰ),得,…………………………12分例4.[2014浙江]已知数列{an}和{bn}满足a1a2a3…an=(n∈N*).若{an}为等比数列,且a1=2,b3=6+b2.(1)求an与bn.(2)设cn=-(n∈N*).记数列{cn}的前n项和为Sn.(i)求Sn;(ii)求正整数k,使得对任意n∈N*,均有Sk≥Sn.解:(1)由a1a2a3…an=,得两式相除,得b3-b2=6,知a3=...