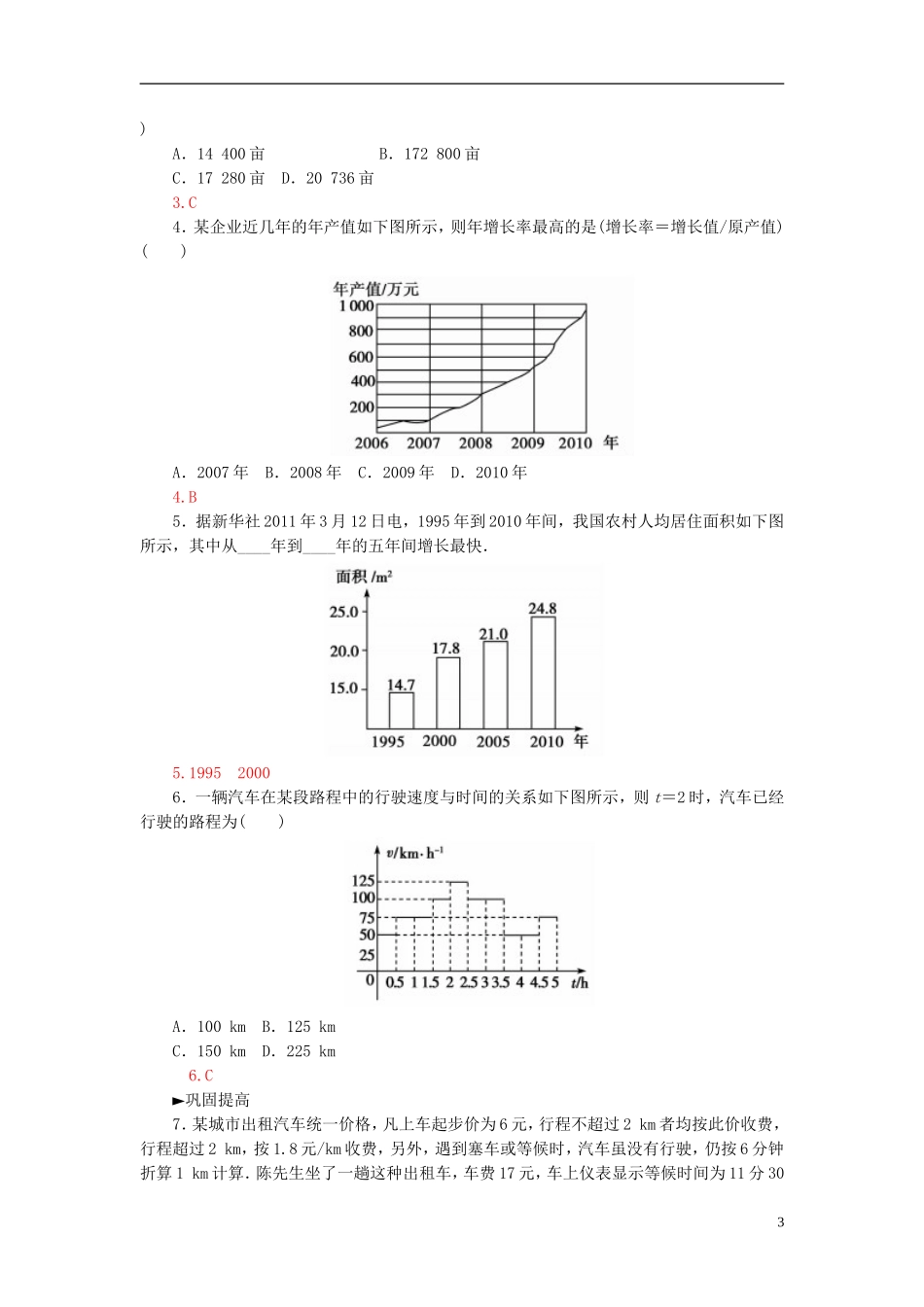
【金版学案】2015-2016高中数学3.2.2几类不同增长的函数模型练习新人教A版必修11.对于函数:幂函数y=xn(n>0)、指数函数y=ax(a>1)、对数函数y=logax(a>1)在区间(0,+∞)上随x增大而增大,衰减速度从大到小的函数依次为____________、____________、____________.因此总存在一个x0,当x>x0时就有________________.例如:y=2x,y=x2与y=log2x的图象在区间(0,+∞)上随x增大而增大,增长速度从大到小的函数依次为____________________.2.对于函数:幂函数y=xn(n<0)、指数函数y=ax(0<a<1)、对数函数y=logax(0<a<1)在区间(0,+∞)上随x增大而减小,减小速度从大到小的函数依次为______________,______________,__________.因此总存在一个x0,当x>x0时就有____________.例如:y=,y=x-2与y=logx的图象在区间(0,+∞)上随x增大而减小,减小速度从大到小的函数依次为______________,基础梳理1.y=ax(a>1)y=xn(n>0)y=logax(a>1)logax0<x<ax0y=2x,y=x2,y=log2x2.y=logax(0<a<1)y=xn(n<0)y=ax(0<a<1)logax0<x<ax0y=logxy=x-2y=1.建立函数模型时常用的分析方法有哪些?解析:建立函数模型常用的分析方法有:关系分析法.即通过寻找关键词和关键量之间的数量关系的方法来建立问题的数学模型的方法;列表分析法,即通过列表的方式探求问题的数学模型的方法;图象分析法,即通过对图象中的数量关系进行分析来建立问题的数学模型的方法.,2.高中与建立函数模型有关的应用题,常涉及物价、路程、产值、环保等实际问题,也涉及角度、面积、体积、造价的最优化问题.解答这类问题的关键在哪?解析:解答这类问题的关键是确切建立相应的函数解析式,然后应用函数、方程和不等式的有关知识加以解决,而正确建立函数解析式,则要合理选取变量,必要时引入其他相关辅助变量,寻找它们之间的内在联系,选用恰当的代数式表示问题中的关系,然后根据已知条件,运用已掌握的数学知识、物理知识及其他相关知识建立关系.1.在某种新型材料的研制中,实验人员获得了下列一组实验数据(见下表).现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是()x1.953.003.945.106.12y0.971.591.982.352.61A.y=2xB.y=log2xC.y=(x2-1)D.y=2.61cosx2.客车从甲地以60km/h的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以80km/h的速度匀速行驶1小时到达丙地,下列描述客车从甲地出发,经过乙地,最后到达丙地所经过的路程s与时间t之间关系的图象中,正确的是()13.在股票买卖过程中,经常用到两种曲线,一种是即时价格曲线y=f(x),一种是平均价格曲线y=g(x)[如f(2)=3表示开始交易后第2小时的即时价格为3元;g(2)=4表示开始交易后两个小时内所有成交股票的平均价格为4元].下面所给出的四个图象中,实线表示y=f(x),虚线表示y=g(x),其中可能正确的是()自测自评1.B2.C3.解析:刚开始交易时,即时价格和平均价格应该相等,A错误;开始交易后,平均价格应该跟随即时价格变动,在任何时刻其变化幅度应该小于即时价格变化幅度,B、D均错误.答案:C►基础达标1.下面对函数f(x)=logx与g(x)=在区间(0,+∞)上的衰减情况说法正确的是()A.f(x)的衰减速度越来越慢,g(x)的衰减速度越来越快B.f(x)的衰减速度越来越快,g(x)的衰减速度越来越慢C.f(x)的衰减速度越来越慢,g(x)的衰减速度越来越慢D.f(x)的衰减速度越来越快,g(x)的衰减速度越来越快1.C2.某工厂8年来某产品的总产量y与时间t(年)的函数关系如下页图所示,下列的说法:①前3年中总产量的增长速度越来越快②前3年中总产量的增长速度越来越慢③第3年后这种产品停止生产④第3年后这种产品的产量保持不变正确的有________(填序号).2.①③3.某林场计划第一年造林10000亩,以后每年比前一年多造林20%,则第四年造林(2)A.14400亩B.172800亩C.17280亩D.20736亩3.C4.某企业近几年的年产值如下图所示,则年增长率最高的是(增长率=增长值/原产值)()A.2007年B.2008年C.2009年D.2010年4.B5.据新华社2011年3月12日电,1995年到2010年间,我国农村人均居住...