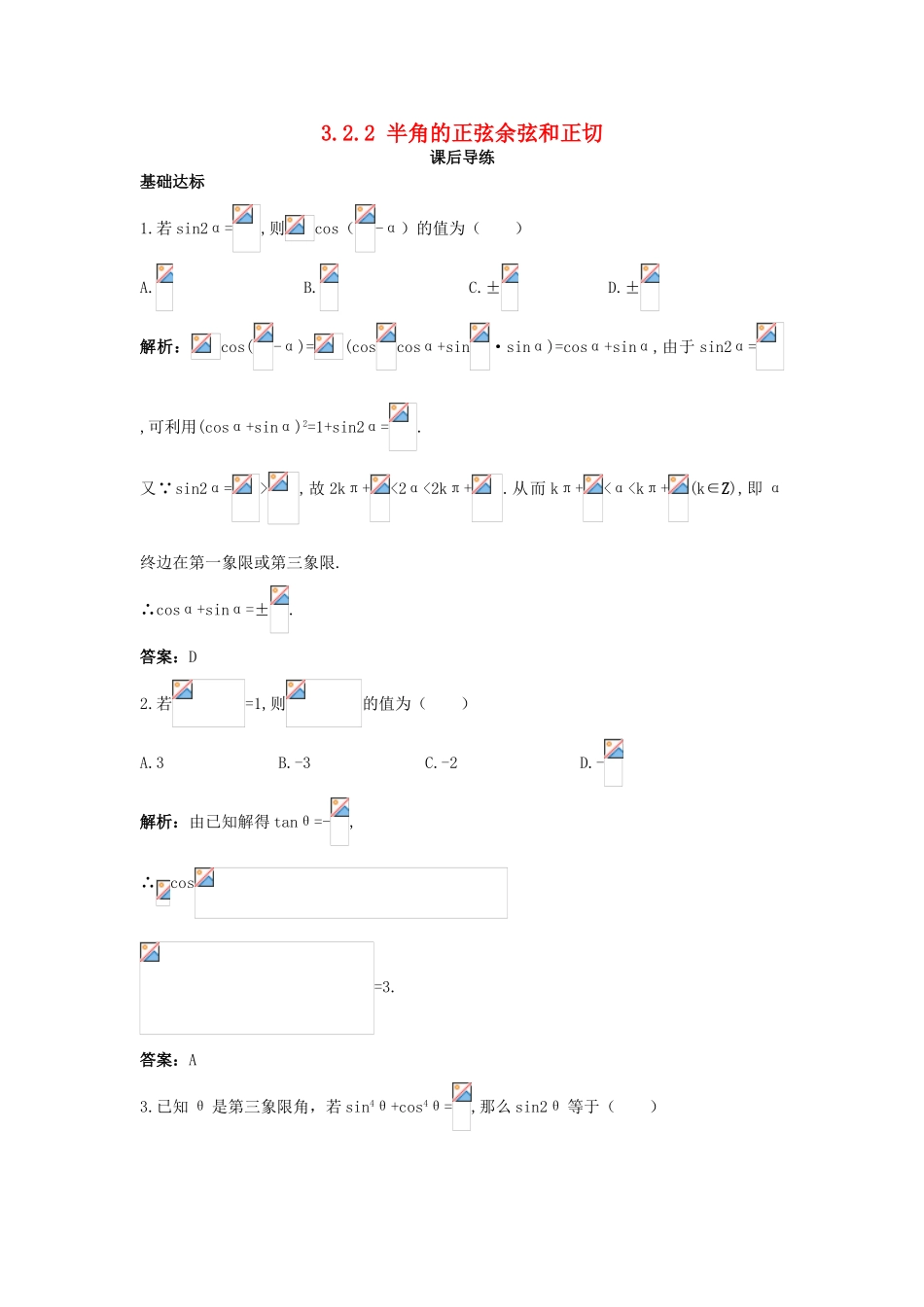
3.2.2半角的正弦余弦和正切课后导练基础达标1.若sin2α=,则cos(-α)的值为()A.B.C.±D.±解析:cos(-α)=(coscosα+sin·sinα)=cosα+sinα,由于sin2α=,可利用(cosα+sinα)2=1+sin2α=.又∵sin2α=>,故2kπ+<2α<2kπ+.从而kπ+<α0,由此知<α+<.∴sin(α+)=,从而有cos2α=sin(2α+)=2sin(α+)cos(α+)=2×()×=.sin2α=-cos(2α+)=1-2cos2(α+)=1-2×()2=.∴cos(2α+)=×()=.拓展探究12.在△ABC中,求证:tantan+tantan+tantan=1.证明:∵A、B、C是△ABC的三个内角,∴A+B+C=π.从而有=-.左边=tan(tan+tan)+tan·tan=tan·tan(+)(1-tan·tan)+tantan=tantan(-)(1-tantan)+tantan=1-tantan+tantan=1=右边.∴等式成立.