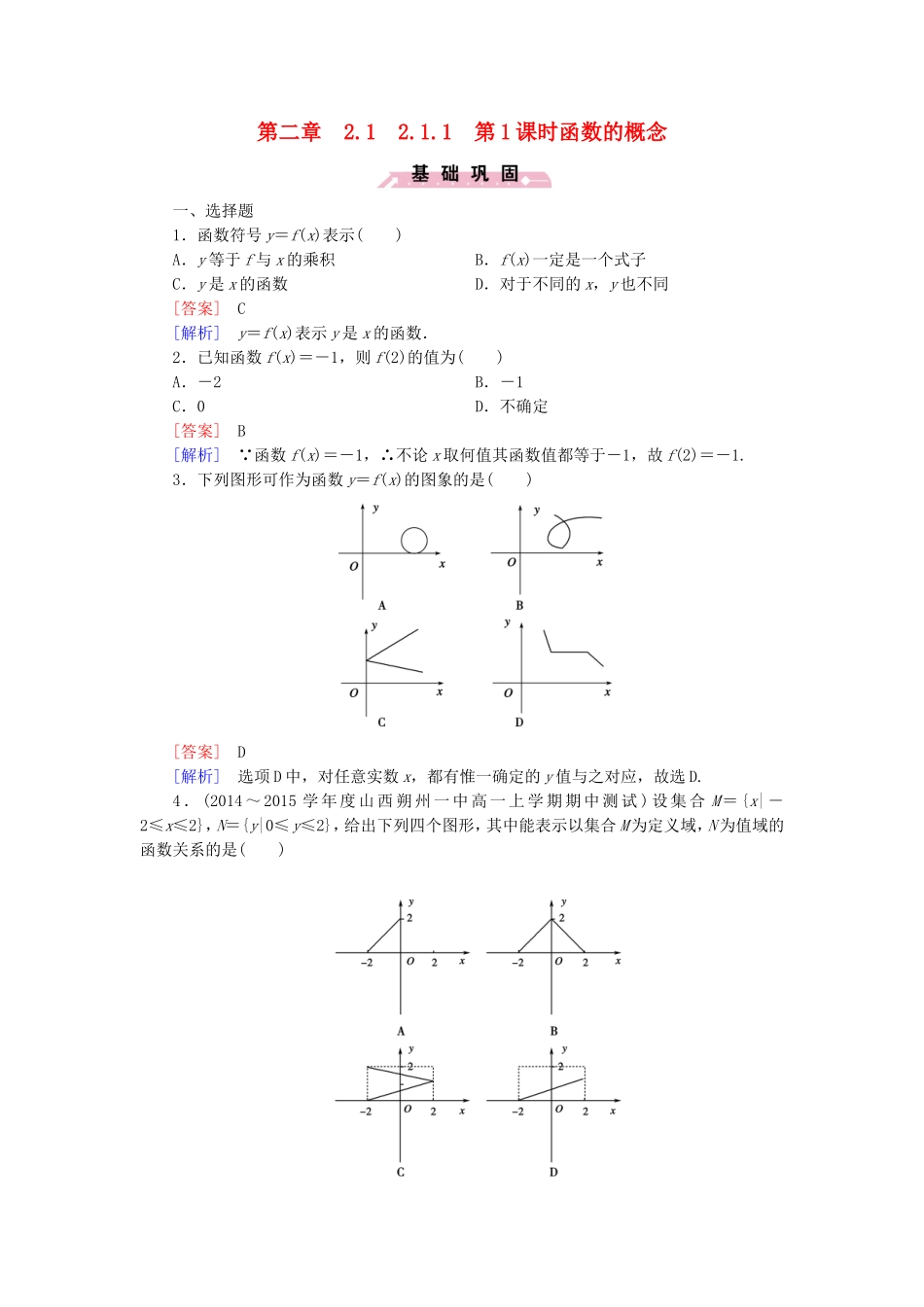
第二章2.12.1.1第1课时函数的概念一、选择题1.函数符号y=f(x)表示()A.y等于f与x的乘积B.f(x)一定是一个式子C.y是x的函数D.对于不同的x,y也不同[答案]C[解析]y=f(x)表示y是x的函数.2.已知函数f(x)=-1,则f(2)的值为()A.-2B.-1C.0D.不确定[答案]B[解析] 函数f(x)=-1,∴不论x取何值其函数值都等于-1,故f(2)=-1.3.下列图形可作为函数y=f(x)的图象的是()[答案]D[解析]选项D中,对任意实数x,都有惟一确定的y值与之对应,故选D.4.(2014~2015学年度山西朔州一中高一上学期期中测试)设集合M={x|-2≤x≤2},N={y|0≤y≤2},给出下列四个图形,其中能表示以集合M为定义域,N为值域的函数关系的是()[答案]B[解析]选项A中,函数的定义域不是集合M;选项C不是函数关系;选项D中,函数的值域不是集合N,故选B.5.(2014~2015学年度四川德阳五中高一上学期月考)已知函数f(x+1)的定义域为(-2,-1),则函数f(x)的定义域为()A.B.(-1,0)C.(-3,-2)D.[答案]B[解析] 函数f(x+1)的定义域为(-2,-1),∴-13.故实数a的取值范围为a>3.一、选择题1.函数f(x)=-5,则f(3)=()A.-3B.4C.-1D.6[答案]A[解析]f(3)=-5=2-5=-3.2.设f(x)=,则=()A.1B.-1C.D.-[答案]B[解析] f(x)=,∴f(2)==,f()===-,∴==-1.3.(2014~2015学年度四川德阳五中高一上学期月考)函数f(x)=+的定义域是()A.B.∪C.D.∪[答案]B[解析]由题意得,解得-3≤x<且x≠-,故选B.4.已知函数f(x)满足2f(x)+f(-x)=3x+2且f(-2)=-,则f(2)=()A.-B.-C.D.[答案]D[解析] 2f(x)+f(-x)=3x+2,∴2f(2)+f(-2)=8,又f(-2)=-,∴f(2)=.二、填空题5.已知函数f(x)=ax2-1(a≠0),且f[f(1)]=-1,则a的取值为________.[答案]1[解析] f(x)=ax2-1,∴f(1)=a-1,f[f(1)]=f(a-1)=a(a-1)2-1=-1,∴a(a-1)2=0,又 a≠0,∴a-1=0,∴a=1.6.(2014~2015学年度湖北部分重点中学高一上学期期中测试)已知f(x-1)的定义域为[-3,3],则f(x)的定义域为____________.[答案][-4,2][解析] -3≤x≤3,∴-4≤x-1≤2,∴f(x)的定义域为[-4,2].三、解答题7.求下列函数的值域:(1)y=2x+1,x∈{1,2,3,4,5};(2)y=+1;(3)y=x2-4x+6,x∈[1,5];(4)y=x+;(5)y=.[解析](1) y=2x+1,且x∈{1,2,3,4,5},∴y∈{3,5,7,9,11}.∴函数的值域为{3,5,7,9,11}.(2) ≥0,∴+1≥1.∴函数的值域为[1,+∞).(3)配方得y=(x-2)2+2, x∈[1,5],由图知2≤y≤11.即函数的值域为[2,11].(4)令u=,则u≥0,x=,∴y=+u=(u+1)2≥.∴函数的值域为[,+∞).(5)y===3+≠3.∴函数的值域为{y|y≠3}.8.(1)已知函数y=f(x+2)的定义域为[1,4],求函数y=f(x)的定义域;(2)已知函数y=f(2x)的定义域为[0,1],求函数y=f(x+1)的定义域;(3)已知函数y=f(x)的定义域为[0,1],求g(x)=f(x+a)+f(x-a)的定义域.[解析](1) y=f(x+2)...