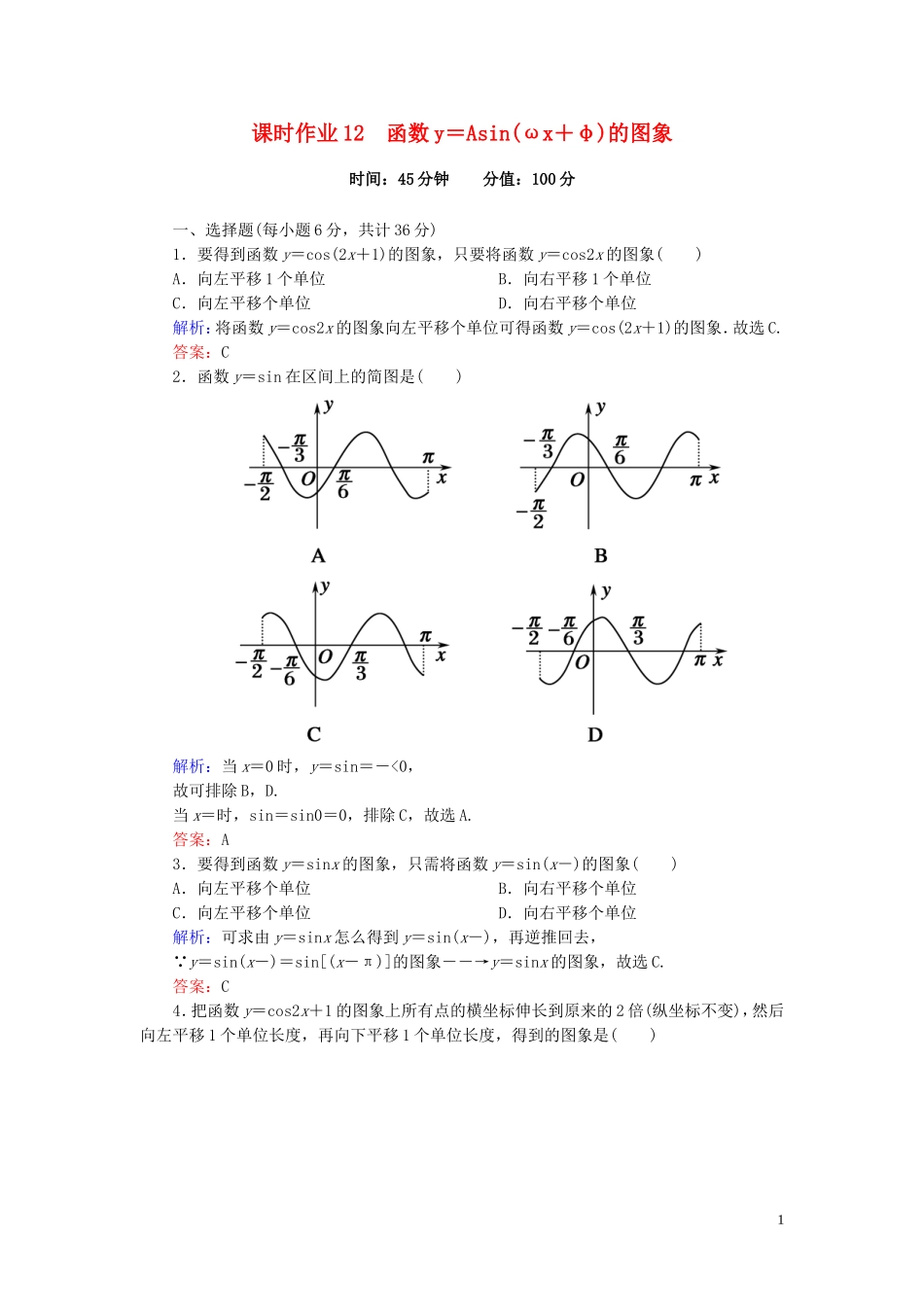
课时作业12函数y=Asin(ωx+φ)的图象时间:45分钟分值:100分一、选择题(每小题6分,共计36分)1.要得到函数y=cos(2x+1)的图象,只要将函数y=cos2x的图象()A.向左平移1个单位B.向右平移1个单位C.向左平移个单位D.向右平移个单位解析:将函数y=cos2x的图象向左平移个单位可得函数y=cos(2x+1)的图象.故选C.答案:C2.函数y=sin在区间上的简图是()解析:当x=0时,y=sin=-<0,故可排除B,D.当x=时,sin=sin0=0,排除C,故选A.答案:A3.要得到函数y=sinx的图象,只需将函数y=sin(x-)的图象()A.向左平移个单位B.向右平移个单位C.向左平移个单位D.向右平移个单位解析:可求由y=sinx怎么得到y=sin(x-),再逆推回去,∵y=sin(x-)=sin[(x-π)]的图象――→y=sinx的图象,故选C.答案:C4.把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图象是()1解析:由题意,y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得解析式为y=cosx+1,向左平移一个单位为y=cos(x+1)+1,向下平移一个单位为y=cos(x+1),显然点(-1,0)在函数图象上.故选A.答案:A5.设函数f(x)=cosωx(ω>0),将y=f(x)的图象向右平移个单位长度后,所得的图象与原图象重合,则ω的最小值等于()A.B.3C.6D.9解析:将y=f(x)的图象向右平移个单位长度后得到y=cos[ω(x-)],所得图象与原图象重合,所以cos(ωx-ω)=cosωx,则-ω=2kπ,得ω=-6k(k∈Z).又ω>0,所以ω的最小值为6,故选C.答案:C6.(2013·福建卷)将函数f(x)=sin(2x+θ)(-<θ<)的图象向右平移φ(φ>1)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P(0,),则φ的值可以是()A.B.C.D.解析:将函数f(x)的图象向右平移φ个单位长度,得g(x)=sin[2(x-φ)+θ],由题意得解得θ=,φ=-kπ或--kπ(k∈Z),结合选项取得φ=.答案:B二、填空题(每小题8分,共计24分)7.把函数y=3sin(2x+)的图象向右平移个单位长度,再向下平移1个单位长度,则得到的函数的解析式是________.解析:函数y=3sin(2x+)的图象向右平移个单位长度得函数y=3sin[2(x-)+]=3sin2x,再向下平移1个单位长度得y=3sin2x-1.答案:y=3sin2x-128.将函数f(x)的图象向右平移个单位长度后,再向上平移1个单位长度得函数y=2sin(4x-)的图象,则f(x)=________.解析:将y=2sin(4x-)的图象向左平移个单位长度,得函数y=2sin[4(x+)-]=2sin(4x+)的图象,再向下平移一个单位长度,得函数y=2sin(4x+)-1的图象,即f(x)=2sin(4x+)-1.答案:2sin(4x+)-19.已知函数f(x)=sin(x∈R,ω>0)的最小正周期为π,为了得到函数g(x)=2sin的图象,只需将y=f(x)的图象上________.答案:各点的纵坐标变为原来的2倍,横坐标变为原来的2倍三、解答题(共计40分,其中10题10分,11、12题各15分)10.由函数y=sinx的图象如何得到y=2cosx的图象?解:由y=sinx=cos(-x)=cos(x-),则由y=cos(x-)的图象得到y=2cosx的图象可由以下方法得到:11.已知函数f(x)=3sin(2x+φ),其图象向左平移个单位长度后,关于y轴对称.(1)求函数f(x)的解析式.(2)说明其图象是由y=sinx的图象经过怎样的变换得到的.解:(1)将函数f(x)=3sin(2x+φ)图象上的所有点向左平移个单位长度后,所得图象的函数解析式为y=3sin[2(x+)+φ]=3sin(2x++φ).因为图象平移后关于y轴对称,所以2×0++φ=kπ+(k∈Z),所以φ=kπ+(k∈Z).因为φ∈(0,),所以φ=.所以f(x)=3sin(2x+).(2)将函数y=sinx的图象上的所有点向左平移个单位长度,所得图象的函数解析式为y=sin(x+),再把所得图象上各点的横坐标缩短到原来的倍(纵坐标不变),得函数y=sin(2x+)的图象,再把图象上各点的纵坐标伸长到原来的3倍(横坐标不变),即得函数y=3sin(2x+)的图象.12.已知函数f(x)=sin+1.(1)求函数y=f(x)的周期、最大值和对称中心;(2)在直角坐标系中画出y=f(x)在[-,]上的图象.解:(1)周期T===π,∵-1≤sin≤1,∴f(x)的最大值是1+.由2x-=kπ(k∈Z).得x=+(k∈Z),∴对称中心为(+,1)(k∈Z).3(2)列表如下:x--f(x)21-11+2函数y=f(x)在上的图象如下图所示.4