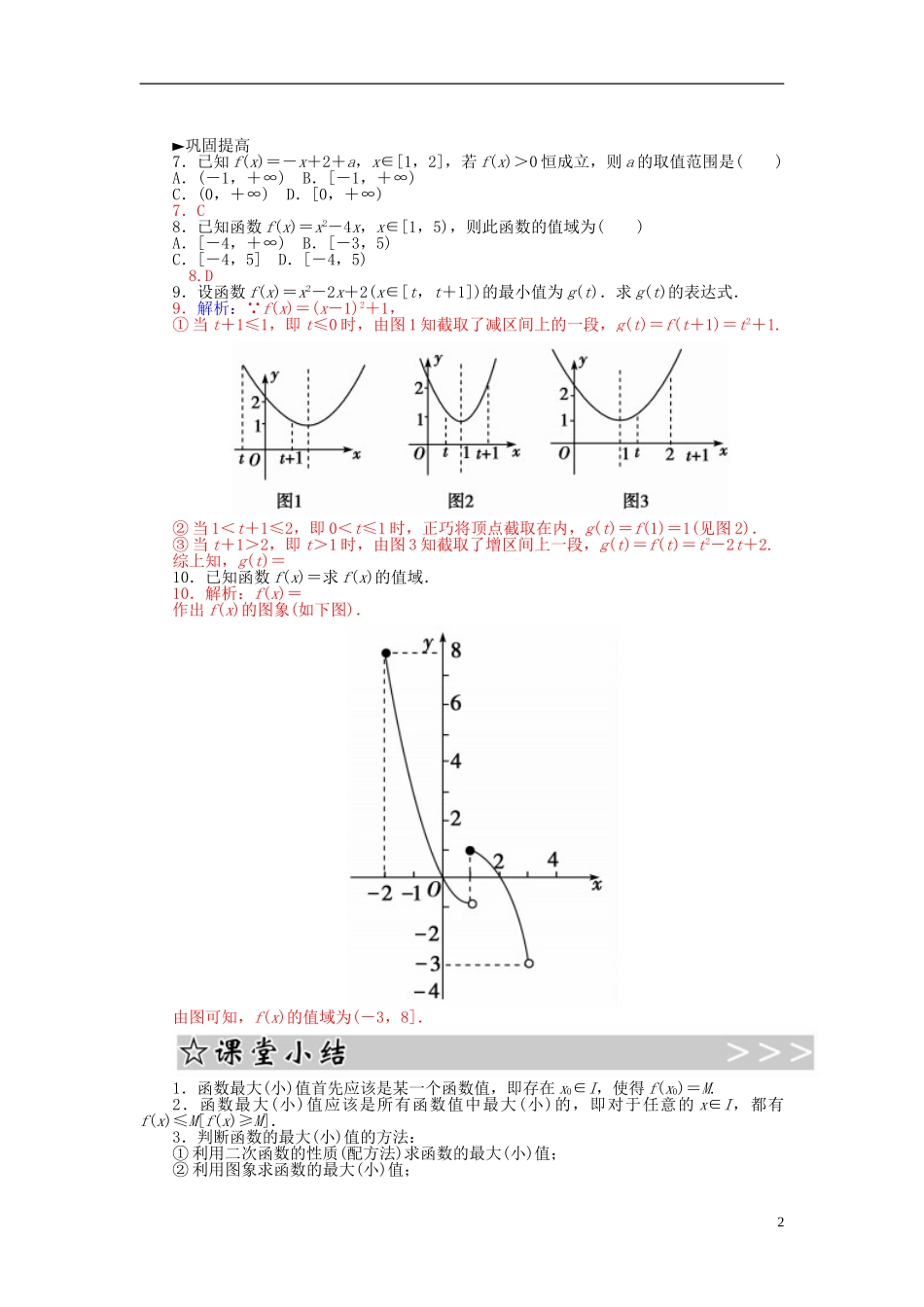
【金版学案】2015-2016高中数学1.3.2函数的最大(小)值练习新人教A版必修11.最大值:一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:①对于任意的x∈I,都有f(x)≤M;②存在x0∈I,使得f(x0)=M.那么,称M是函数y=f(x)的最大值.2.最小值:一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:①对于任意的x∈I,都有f(x)≥M;②存在x0∈I,使得f(x0)=M.那么,称M是函数y=f(x)的最小值.例如:已知函数f(x)=2x2-1,求函数f(x)当x∈(-1,2]时的最大值与最小值.基础梳理2.最大值为f(2)=7,最小值为f(0)=-1,1.函数的最大(小)值对应在图象上表示成什么?解析:函数的最大(小)值,实际上是函数图象的最高(低)点的纵坐标,因而借助函数图象的直观性,可得到函数最值.2.若函数f(x)满足:对定义域中的任意x都有f(x)≥f(2),能说函数f(x)的最小值是f(2)吗?解析:由最小值的定义可知函数f(x)的最小值是f(2).但取得最小值时x的值除x=2外,可能还有别的值.3.若二次函数f(x)满足:对定义域中的任意x都有f(x)≤f(0),你能判断二次函数f(x)的对称轴和开口方向吗?解析:由f(x)≤f(0)知当x=0时,f(x)取最大值,故函数f(x)的对称轴是直线x=0,即y轴,且开口向下.1.函数y=-2x+1在区间上的最大值是____,最小值是____.2.函数y=-在区间[2,7]上的最大值、最小值分别是()A.0,-B.0,-C.-,-D.-,-3.函数y=x2-2x+4的最小值为____.4.函数f(x)=(x∈R)的最大值是____,最小值________.自测自评1.5-32.D3.34.1不存在►基础达标1.函数y=在[2,3]上的最小值为()A.2B.C.D.-1.B2.函数f(x)=的最大值是()A.B.C.D.2.D3.已知函数f(x)=x2-2,其中x∈[0,2],这个函数的最大值和最小值分别为()A.-2和1B.2和-2C.2和-1D.-1和23.解析:∵f(x)=x2-2,x∈[0,2]是单调递增函数,∴ymax=f(2)=2,ymin=f(0)=-2.答案:B4.已知函数f(x)=x2-6x+8,x∈[1,a],并且f(x)的最小值为f(a),则实数a的取值范围是________________________________________________________________________.4.解析:由题意知,f(x)在[1,a]上是单调递减的,又∵f(x)的单调递减区间为(-∞,3],∴1<a≤3.答案:(1,3]5.已知f(x+4)=4x2+4x+3(x∈R),那么函数f(x)的最小值为________.5.解析:∵f(x+4)=4x2+4x+3,设x+4=t,则x=t-4,∴f(t)=4(t-4)2+4(t-4)+3=4t2-28t+51.∴f(x)=4x2-28x+51=4+2,∴f(x)min=2.6.已知0<t≤,那么-t的最小值是()A.B.C.2D.-26.解析:∵y=-t在上为减函数,∴t=时y有最小值.答案:1►巩固提高7.已知f(x)=-x+2+a,x∈[1,2],若f(x)>0恒成立,则a的取值范围是()A.(-1,+∞)B.[-1,+∞)C.(0,+∞)D.[0,+∞)7.C8.已知函数f(x)=x2-4x,x∈[1,5),则此函数的值域为()A.[-4,+∞)B.[-3,5)C.[-4,5]D.[-4,5)8.D9.设函数f(x)=x2-2x+2(x∈[t,t+1])的最小值为g(t).求g(t)的表达式.9.解析:∵f(x)=(x-1)2+1,①当t+1≤1,即t≤0时,由图1知截取了减区间上的一段,g(t)=f(t+1)=t2+1.②当1<t+1≤2,即0<t≤1时,正巧将顶点截取在内,g(t)=f(1)=1(见图2).③当t+1>2,即t>1时,由图3知截取了增区间上一段,g(t)=f(t)=t2-2t+2.综上知,g(t)=10.已知函数f(x)=求f(x)的值域.10.解析:f(x)=作出f(x)的图象(如下图).由图可知,f(x)的值域为(-3,8].1.函数最大(小)值首先应该是某一个函数值,即存在x0∈I,使得f(x0)=M.2.函数最大(小)值应该是所有函数值中最大(小)的,即对于任意的x∈I,都有f(x)≤M[f(x)≥M].3.判断函数的最大(小)值的方法:①利用二次函数的性质(配方法)求函数的最大(小)值;②利用图象求函数的最大(小)值;2③利用函数单调性判断函数的最大(小)值.4.如果函数y=f(x)(x∈[a,c])在区间[a,b]上单调递增,在区间[b,c]上单调递减,则函数y=f(x)在x=b处有最大值f(b).5.如果函数y=f(x)(x∈[a,c])在区间[a,b]上单调递减,在区间[b,c]上单调递增,则函数y=f(x)在x=b处有最小值f(b).3