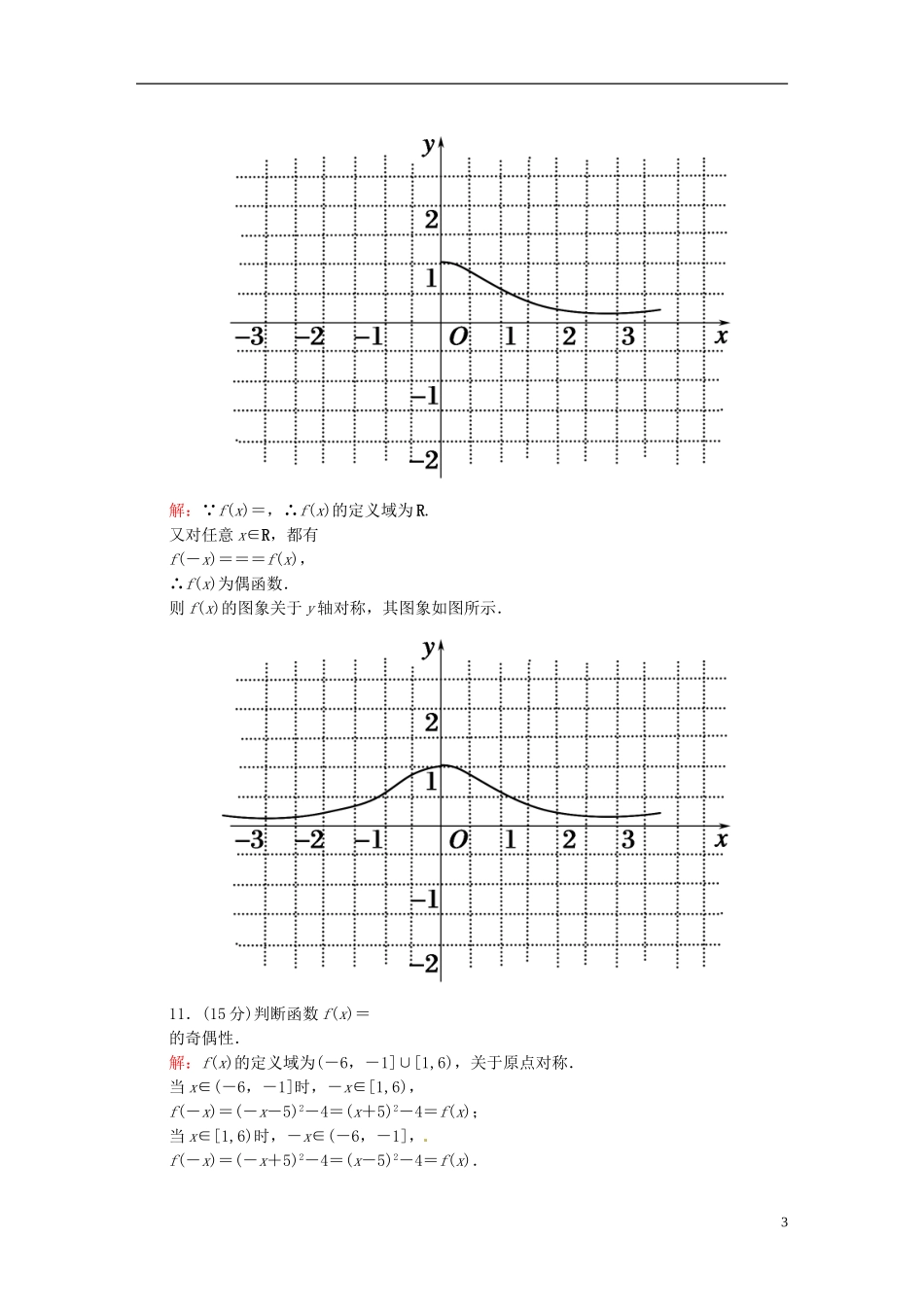
课时作业12函数奇偶性的概念时间:45分钟分值:100分一、选择题(每小题6分,共计36分)1.给定四个函数:①y=x3+;②y=(x>0);③y=x3+1;④y=,其中是奇函数的有()A.1个B.2个C.3个D.4个解析:①④为奇函数.答案:B2.奇函数y=f(x)(x∈R)的图象必定经过点()A.(a,f(-a))B.(-a,f(a))C.(-a,-f(a))D.(a,f())解析:∵y=f(x)是奇函数,∴f(-a)=-f(a).∴选C.答案:C3.设f(x)是定义在R上的奇函数,当x≤0时,f(x)=2x2-x,则f(1)=()A.-3B.-1C.1D.3解析:∵x≤0时,f(x)=2x2-x,∴f(-1)=2×(-1)2-(-1)=3.∵f(x)是奇函数,∴f(-1)=-f(1),即f(1)=-f(-1)=-3.答案:A4.函数f(x)=是()A.奇函数B.偶函数C.既是奇函数又是偶函数D.非奇非偶函数解析:若x是有理数,则-x也是有理数,∴f(-x)=f(x)=1;若x是无理数,则-x也是无理数,∴f(-x)=f(x)=0.所以函数f(x)是偶函数.答案:B5.若函数f(x)是奇函数,则f(1+)+f=()A.-1B.0C.1D.2解析:==-(1+).∵f(x)是奇函数,∴f=f[-(1+)]=-f(1+).∴f(1+)+f=0.选B.答案:B6.设f(x)是R上的任意函数,则下列叙述正确的是()1A.f(x)f(-x)是奇函数B.f(x)|f(-x)|是奇函数C.f(x)-f(-x)是偶函数D.f(x)+f(-x)是偶函数解析:用奇偶性定义判断.设g(x)=f(x)+f(-x),则g(-x)=f(-x)+f(x)=g(x),∴f(x)+f(-x)是偶函数,∴选D.答案:D二、填空题(每小题8分,共计24分)7.设函数y=f(x)是奇函数.若f(-2)+f(-1)-3=f(1)+f(2)+3,则f(1)+f(2)=________.解析:∵f(x)是奇函数,∴f(-2)=-f(2),f(-1)=-f(1).又f(-2)+f(-1)-3=f(1)+f(2)+3,∴f(1)+f(2)=-3.答案:-38.已知函数f(x)=ax2+bx+c(-2a-3≤x≤1)是偶函数,则a=________,b=________.解析:∵f(x)是偶函数,∴其定义域关于原点对称.∴-2a-3=-1.∴a=-1.∴f(x)=-x2+bx+c.∵f(-x)=f(x),∴-(-x)2+b(-x)+c=-x2+bx+c.∴-b=b,∴b=0.答案:-109.已知函数y=f(x)是偶函数,其图象与x轴有四个交点,则方程f(x)=0的所有实根之和是________.解析:偶函数y=f(x)的图象关于y轴对称,∴f(x)与x轴的四个交点也关于y轴对称.因此,若一根为x1,则它关于y轴对称的根为-x1;若一根为x2,则它关于y轴对称的根为-x2,故f(x)=0的四根之和为x1+(-x1)+x2+(-x2)=0.答案:0三、解答题(共计40分)10.(10分)已知函数f(x)=在区间[0,+∞)上的图象如图所示,请据此在该坐标系中补全函数f(x)在定义域内的图象,请说明你的作图依据.2解:∵f(x)=,∴f(x)的定义域为R.又对任意x∈R,都有f(-x)===f(x),∴f(x)为偶函数.则f(x)的图象关于y轴对称,其图象如图所示.11.(15分)判断函数f(x)=的奇偶性.解:f(x)的定义域为(-6,-1]∪[1,6),关于原点对称.当x∈(-6,-1]时,-x∈[1,6),f(-x)=(-x-5)2-4=(x+5)2-4=f(x);当x∈[1,6)时,-x∈(-6,-1],f(-x)=(-x+5)2-4=(x-5)2-4=f(x).3综上可知,对于x∈(-6,-1]∪[1,6),都有f(-x)=f(x),所以f(x)=是偶函数.——能力提升——12.(15分)已知函数f(x)=是奇函数,且f(2)=.(1)求p,q的值;(2)判断f(x)在(1,+∞)上的单调性.解:(1)由奇函数定义,得f(-x)=-f(x),即=-.∴-3x+q=-3x-q,∴2q=0,∴q=0.又f(2)=,∴=,解得p=2,∴p=2,q=0.(2)f(x)==(x+).设11,∴上式<0,即f(x1)