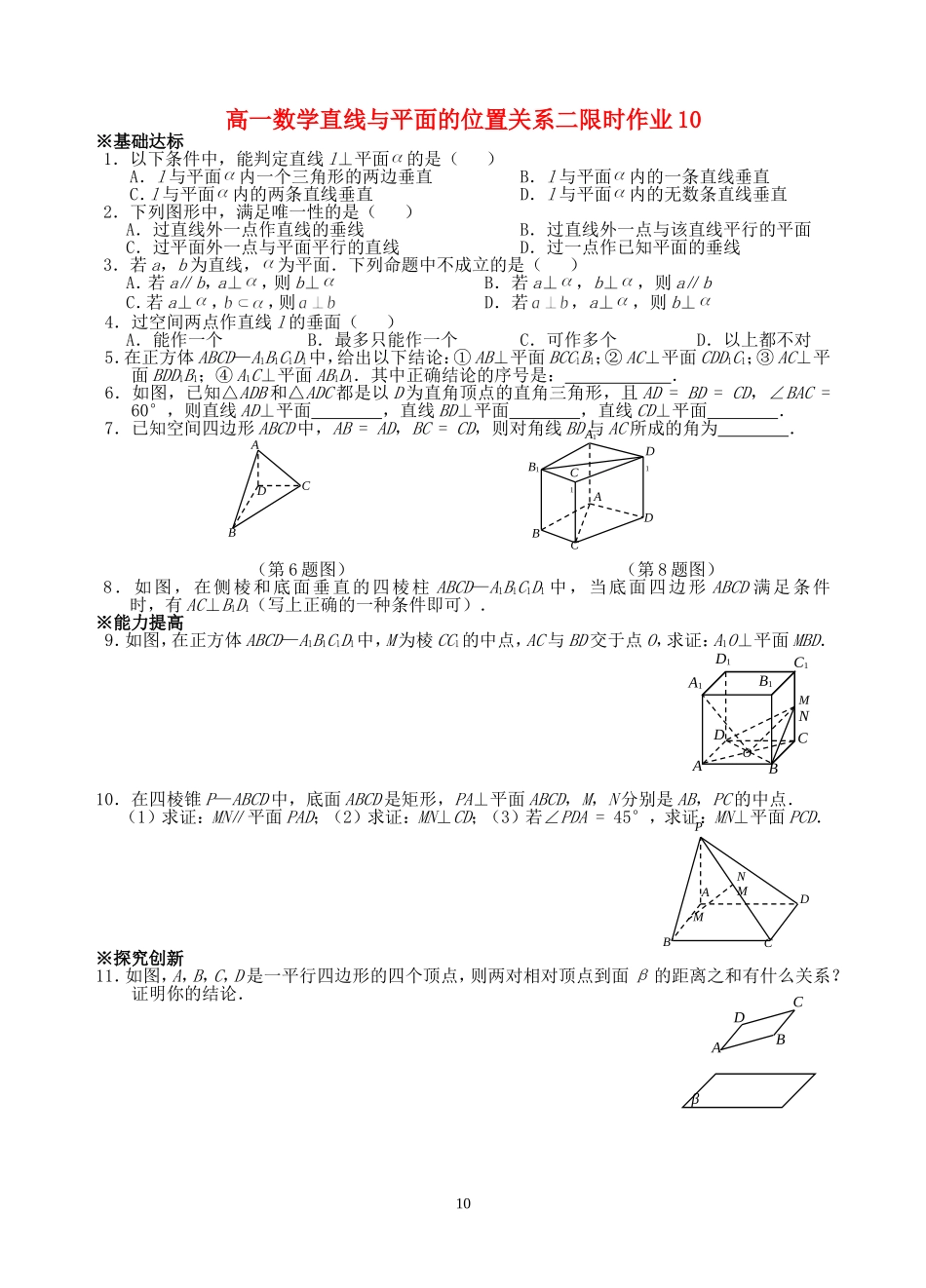
ABCD高一数学直线与平面的位置关系二限时作业10※基础达标1.以下条件中,能判定直线l⊥平面的是()A.l与平面内一个三角形的两边垂直B.l与平面内的一条直线垂直C.l与平面内的两条直线垂直D.l与平面内的无数条直线垂直2.下列图形中,满足唯一性的是()A.过直线外一点作直线的垂线B.过直线外一点与该直线平行的平面C.过平面外一点与平面平行的直线D.过一点作已知平面的垂线3.若a,b为直线,为平面.下列命题中不成立的是()A.若a∥b,a⊥,则b⊥B.若a⊥,b⊥,则a∥bC.若a⊥,,则D.若,a⊥,则b⊥4.过空间两点作直线l的垂面()A.能作一个B.最多只能作一个C.可作多个D.以上都不对5.在正方体ABCD—A1B1C1D1中,给出以下结论:①AB⊥平面BCC1B1;②AC⊥平面CDD1C1;③AC⊥平面BDD1B1;④A1C⊥平面AB1D1.其中正确结论的序号是:.6.如图,已知△ADB和△ADC都是以D为直角顶点的直角三角形,且AD=BD=CD,∠BAC=60°,则直线AD⊥平面,直线BD⊥平面,直线CD⊥平面.7.已知空间四边形ABCD中,AB=AD,BC=CD,则对角线BD与AC所成的角为.(第6题图)(第8题图)8.如图,在侧棱和底面垂直的四棱柱ABCD—A1B1C1D1中,当底面四边形ABCD满足条件时,有AC⊥B1D1(写上正确的一种条件即可).※能力提高9.如图,在正方体ABCD—A1B1C1D1中,M为棱CC1的中点,AC与BD交于点O,求证:A1O⊥平面MBD.10.在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点.(1)求证:MN∥平面PAD;(2)求证:MN⊥CD;(3)若∠PDA=45°,求证:MN⊥平面PCD.※探究创新11.如图,A,B,C,D是一平行四边形的四个顶点,则两对相对顶点到面β的距离之和有什么关系?证明你的结论.10ABCDA1B1C1D1ABCDA1B1C1D1OMNPABCDMNMABCDβ