高一数学正切函数的图象和性质通用版VIP免费

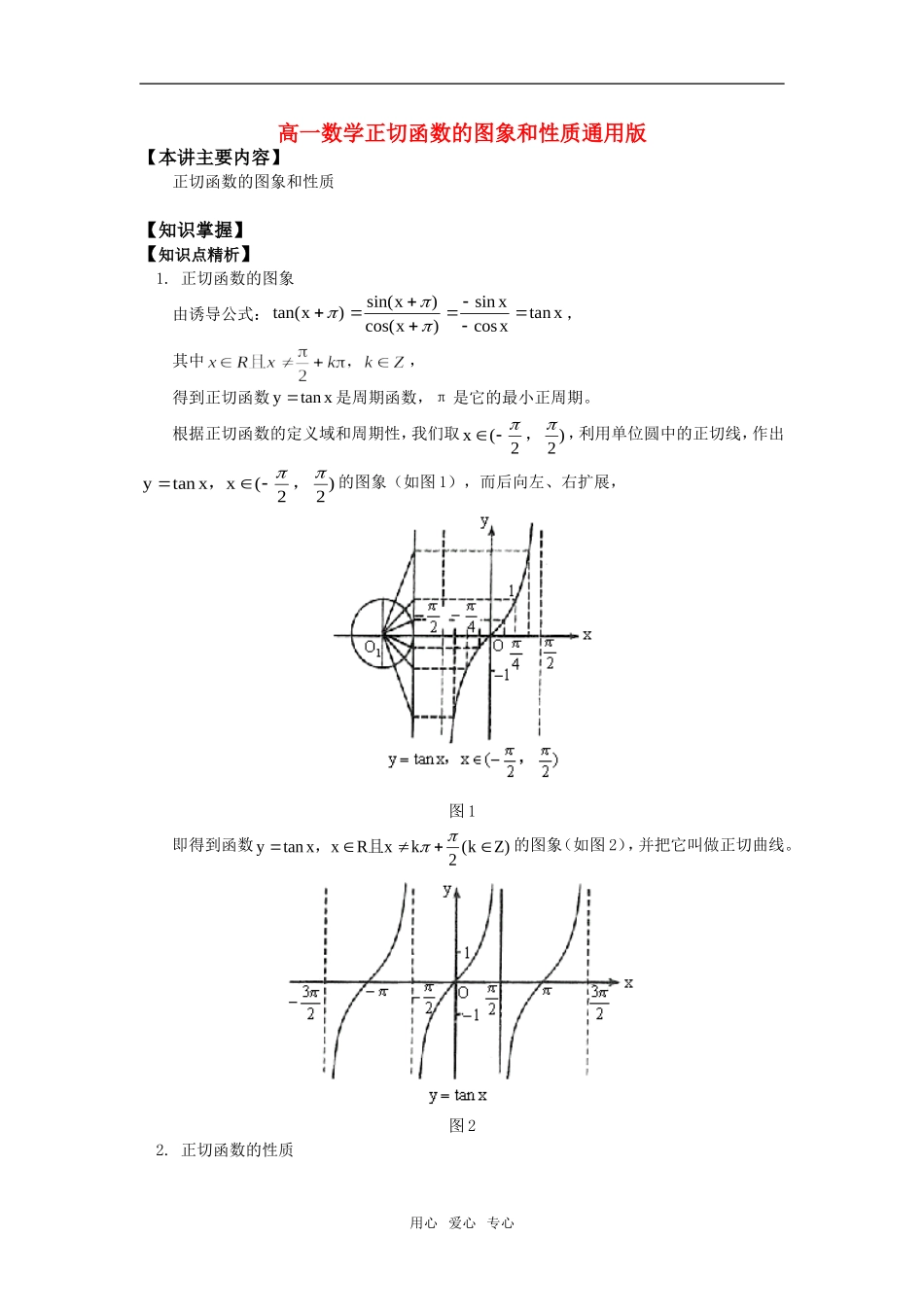
高一数学正切函数的图象和性质通用版【本讲主要内容】正切函数的图象和性质【知识掌握】【知识点精析】1.正切函数的图象由诱导公式：tan()sin()cos()sincostanxxxxxx，其中，得到正切函数yxtan是周期函数，π是它的最小正周期。根据正切函数的定义域和周期性，我们取x()22，，利用单位圆中的正切线，作出yxxtan()，，22的图象（如图1），而后向左、右扩展，图1即得到函数yxxRxkkZ)tan(，且2的图象（如图2），并把它叫做正切曲线。图22.正切函数的性质用心爱心专心（1）定义域：{|}xxRxkkz且，2。（2）值域：R，函数无最大值、最小值。（3）周期性：tan()tanxx，是周期函数，周期是π。（4）奇偶性：tan()tanxx，是奇函数，图像关于原点对称。（5）单调性：在每一个开区间()kkkz22，，内均为增函数。注意：正切函数yxxkkkztan()()，，22是单调增函数，但不能说函数在其定义域内是单调增函数。（6）对称性：正切函数y=tanx是中心对称图形，其对称中心的坐标是()k20，（kZ）。3.本节应重点掌握的内容：（1）正切函数y=tanx的定义域为；值域为R。（2）正切函数yxtan的图象是由互相平行的直线xkkZ)2(隔开的无穷多支曲线组成的，在相邻两条平行线之间的图象是连续变化的。（3）正切函数y=tanx在每一个开区间（kk22，）(kZ)上是增函数，但不能说正切函数在其定义域内是增函数。（4）正切函数y=tanx的最小正周期是π，则函数yAxtan()的最小正周期是||。（5）正切函数y=tanx是奇函数，其图象关于原点对称。【解题方法指导】例1.求函数yxx212logtan的定义域。分析：函数有意义需满足：二次根式中被开方数非负；对数的真数大于0；正切函数本身要有意义。因此需要列出符合条件的不等式组，然后利用数轴或者图象求出它们的公共解集解：由题意得：2000204212logtan(xxxxkkZxkxkkZ)（），对k赋值，在数轴上可得：024xx或∴函数的定义域为：评述：在三角函数中求函数定义域的方法与在函数中求定义域的方法基本一致，只不过用心爱心专心要注意：三角函数本身对自己的约束。例2.求下列函数的最大值，最小值及使函数取得这些值的x的集合。（1）yxxtantan2234（2）yxxsinsin2234分析：化简可得到关于tanx和sinx的二次函数，利用二次函数求最值的方法去求解即可。解：（1）yxxxtantan(tan)2223431 tanx可取所有实数∴函数y没有最大值当tanx3时，即xkkZ3（）时函数y有最小值，ymin1（2）yxxxsinsin(sin)2223431当sinx=1时，即xkkZ)22(时，函数y有最小值ymin()1315232当sinx1时，即xkkZ)22(时，函数y有最大值ymax()1315232评述：本题（1）是关于tanx的二次函数，由于tanx的值域是R，所以可以按一般二次函数yaxbxc2，求它的最值即可。本题（2）是关于sinx的二次函数，由于|sin|x1，∴sinx取不到3，所以函数的最小值不是()3312，而是()1312。当sinx1时，函数的最大值是()1312。例3.已知，正切函数yAxAtan()||（，，）002的图象与x轴相交的两相邻点的坐标为()()60560，和，，且过点（0，－3）。求它的表达式。分析：先由题意确定周期T后，求ω值；再列出A，的方程即可求解。解： 函数yAxtan()的图象与x轴相交的两相邻点的坐标为()60，和()560，用心爱心专心TTyAx566233232又 tan()根据题意，列出方程组AAAtan()tan()tan()tan32603203403即||243A故所求函数表达式为：yx3324tan()评述：确定函数yAxtan()的解析式时，要正确运用正切函数的有关性质，如周期性。确定时，一般用特殊点坐标代入解析式后，解方程求出值。【考点突破】...